2017202110104-高级软件工程第二次作业个人项目之-四则运算生成程序

GitHub项目地址

https://github.com/Cynnn/Arithmatic

PSP2.1表格

PSP2.1	Personal Software Process Stages	预估耗时(分钟)	实际耗时（分钟）
Planning	计划	10	15
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发	670	998
· Analysis	· 需求分析 (包括学习新技术)	60	90
· Design Spec	· 生成设计文档	30	30
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	8
· Design	· 具体设计	60	60
· Coding	· 具体编码	360	600
· Code Review	· 代码复审	60	90
· Test	· 测试（自我测试，修改代码，提交修改）	90	120
Reporting	报告	100	150
· Test Report	· 测试报告	40	60
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40	60
合计		780	1163

一、项目描述与实现功能

---

1. 从《构建之法》第一章的 “程序” 例子出发，完成一个能自动生成小学四则运算题目的命令行 “软件”。

2. 实现的功能有：

• 随机生成四则运算题目，操作数、运算符的种类和顺序都随机生成。
• 支持整数和真分数的四则运算。
• 能处理用户的输入，并判断对错，打分统计正确率。
• 可以使用 -n 参数控制生成题目的个数。
• 支持带括号的多元复合运算
• 运算符个数随机生成（考虑小学生运算复杂度，范围在1~10）。

二、解题思路

---

1. 解题步骤

看到这个题目，我首先想到的是在《数据结构》课程中利用栈操作来对多项式进行求值，接下来，通过对其他需要实现的功能分析过后，我按照以下循序渐进的步骤来完成本次项目：

整数四则运算 ----> 支持真分数运算 ----> 随机生成四则运算式 ----> 判断用户输入对错并打分

2. 核心问题：

• 中缀表达式求值
  之前学过的中缀表达式求值是利用栈先将其变为后缀表达式，再进行求值。我抱着有没有更简单易懂的方法的想法在网上搜索资料，然后看到了老师在博客留言中分享的链接（http://hczhcz.github.io/2014/02/27/shunting-yard-algorithm.html），其中谈到了调度场算法，学习过后我认为非常值得一试，于是本项目中主要用到的就是调度场算法的思想。
  调度场算法：建立运算符和操作数两个堆栈，从左向右扫描表达式，遇到数字进行压栈操作。若遇到符号，则判断其与栈顶符号的优先级，是右括号或者优先级低于栈顶符号，则栈顶元素依次出栈并进行计算，并将当前符号进栈，计算出的数字作为操作数也进行压栈操作，一直到运算符栈的栈为空，则操作数栈的栈顶元素出栈为最终结果。
• 分数运算
  对于分数运算的问题，我的处理方法是：自定义一个分数类（包括分子和分母），对于整数和分数，都当作分数来处理（整数的分母为1）。先根据简单粗暴的运算法则计算出结果，最后再约分。
• 随机生成带括号的四则运算式
  这是我最后一个完成的功能，之前把生成括号考虑的太简单，真正实现起来才意识到有很多限制条件。最终我采用的方法是：
  • 从左到右扫描操作数，通过随机数决定是否生成左括号，如果生成左括号，则再此操作数的后面选择一个操作数生成右括号。
  • 同理，从右到左扫描操作数，通过随机数决定是否生成右括号，如果生成右括号，则在此操作数的前面选择一个操作数生成左括号。
  • 需要注意的是：在此我定义了左括号标记数组和右括号标记数组，对某个操作数添加左括号（右括号）必须在其没有右括号（左括号）的情况下才能添加。

三、设计实现过程

---

1. 类和方法定义

Class	Method	Description
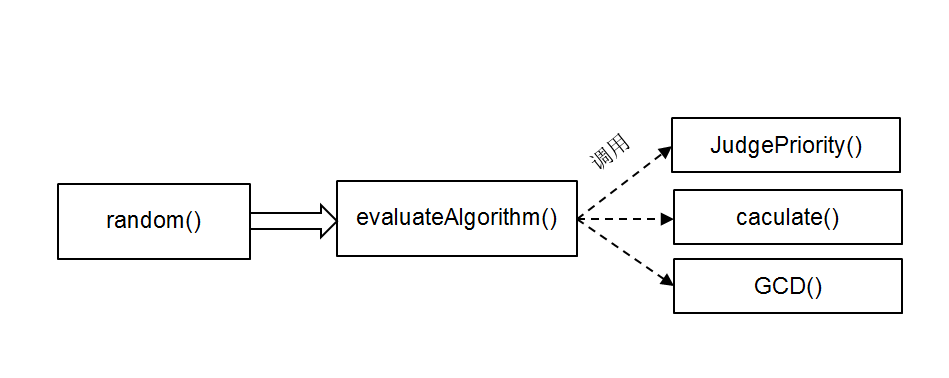
Evaluate类	main()	main()方法
	evaluateAlgorithm()	调度场算法
	JudgePriority()	判断优先级
	caculate()	四则运算法则
	GCD()	辗转相除法对分数约分
	random()	随机生成四则运算式
Fraction类	Fraction()	构造方法

2. 主要数据结构

Stack<Character> ops = new Stack<Character>();    //运算符栈
Stack<Fraction> vals = new Stack<Fraction>();	  //操作数栈
String[] op = new String[opnumber];               //运算符数组
String[] val = new String[valnumber];             //操作数数组

3. 实现过程

4.运行结果

• 考虑到小学生的计算能力，在此设置的操作数取值范围为：0_{10；运算符的数量为1}10。
  

四、关键代码说明

---

• 调度场算法

public static String evaluateAlgorithm(String s) {
		Stack<Character> ops = new Stack<Character>();  //运算符栈
		Stack<Fraction> vals = new Stack<Fraction>();	//操作数栈
		for(int i=0;i<s.length();i++) {
			char s1 = s.charAt(i);
		//左括号入栈 
		if (s1 == '(') 
			ops.push(s1);
		//右括号把之前的数和运算符出栈进行运算
		else if(s1 == ')') {
			while(ops.peek()!= '(') {
				int result[] = new int[2];
				Fraction a = vals.pop();
				Fraction b = vals.pop();
				result = caculate(ops.pop(),a.getNumerator(),a.getDenominator(),b.getNumerator(),b.getDenominator());
				vals.push(new Fraction(result[0],result[1]));
			}

			ops.pop();
		}
		else if(s1 == '+' || s1 == '-' || s1 == '*' || s1 == '÷') {  //遇到运算符的情况
			while(!ops.empty() && JudgePriority(s1,ops.peek())) {    //判断运算符的优先级
				int result[] = new int[2];
				Fraction a = vals.pop();
				Fraction b = vals.pop();
				//当前运算符如果比栈顶运算符的优先级高，将之前的运算符和数字出栈进行运算
				result = caculate(ops.pop(),a.getNumerator(),a.getDenominator(),b.getNumerator(),b.getDenominator()); 
				vals.push(new Fraction(result[0],result[1]));  //将计算出的数字入栈				
			}

			ops.push(s1);
		}
		else {
			if (s1 >= '0' && s1 <= '9') {     //操作数入栈
				StringBuffer buf = new StringBuffer();
				while (i < s.length() && ((s.charAt(i) >='0' && s.charAt(i) <= '9') || s.charAt(i) == '/')) 
					buf.append(s.charAt(i++));								
			i--;
			String s2 = buf.toString();
			int flag = s2.length();
			for(int j=0;j<s2.length();j++) {  //寻找分号的位置
				if(s2.charAt(j) == '/') 
					flag = j;
				}
			StringBuffer buf1 = new StringBuffer();
			StringBuffer buf2 = new StringBuffer();
			for(int k=0;k<flag;k++) {        //分号之前的是分子
				buf1.append(s2.charAt(k));
			}
			if(flag != s2.length() ) {       //分号后面是分母
				for(int k=flag+1;k<s2.length();k++)
					buf2.append(s2.charAt(k));			
				
			}
			//整数的分母是1
			else buf2.append('1');
            //入栈
			vals.push(new Fraction(Integer.parseInt(buf1.toString()),Integer.parseInt(buf2.toString())));
			}
		} 
		}
		while(!ops.empty()) {
			int result[] = new int[2];
			Fraction a = vals.pop();
			Fraction b = vals.pop();
			result = caculate(ops.pop(),a.getNumerator(),a.getDenominator(),b.getNumerator(),b.getDenominator());
			vals.push(new Fraction(result[0],result[1]));
		}
		
         Fraction result = vals.pop();
         //最大公约数
         int k = GCD(result.numerator,result.denominator);
         //如果分母为1，只输出分子
         String rightResult;
         if(result.denominator/k == 1) {
             rightResult = result.numerator/k + "";
         }
         else { //输出分数
        	 rightResult = result.numerator/k+"/"+result.denominator/k + "";
         }
         return rightResult;
		
	}

• 四则运算法则（由于随机生成操作数时限制了不能为0，所以在此没有考虑除数为0的情况）

//对numerator1/denominator1和numerator2/denominator2两个操作数进行运算
public  static int[] caculate(char op, int numerator1, int denominator1, int numerator2, int denominator2) { 
		int[] result = new int[2];
		switch (op) {
		case '+': 
			result[0] = numerator1*denominator2 + numerator2*denominator1; result[1]= denominator1*denominator2;
			return result;
		case '-':
			result[0] = numerator2*denominator1 - numerator1*denominator2; result[1]= denominator1*denominator2;
			return result;
		case '*':
			result[0] = numerator1*numerator2; result[1] = denominator1*denominator2;
			return result;
		case '÷':
			result[0] = numerator2*denominator1; result[1] = numerator1*denominator2;
			return result;
		}
		return result;
	}

• 随机生成带括号的四则运算式

int m = (int)(Math.random()*10) % 2;
		if(m == 0) { //产生带括号的运算式
			int o = (int)(Math.random()*10) % 2;
			if (o == 0) { //先插入左括号，再插入右括号
				int[] lval1 = new int[valnumber]; //左括号标记数组
				int[] rval1 = new int[valnumber]; //右括号标记数组
				for (int k=0;k<valnumber-1;k++) {					
					int n = (int)(Math.random()*10) % 2;
					if(n == 0 && rval1[k] != 1) {
						lval1[k] = 1;           //标记为有左括号
						val[k] = "(" + val[k];  //操作数之前加上左括号
						int c = valnumber - 1;
						//找右括号的位置，必须在左括号的后面
						int d = bracket1.nextInt(c)%(c-k) + (k+1);
						//如果当前操作数之前有左括号，需要重新生成运算式
						while (lval1[d] == 1) 
							d = bracket1.nextInt(c)%(c-k) + (k+1);
						val[d] = val[d] +")";
						rval1[d] = 1;          //标记为有右括号
					} 
				}
			} 

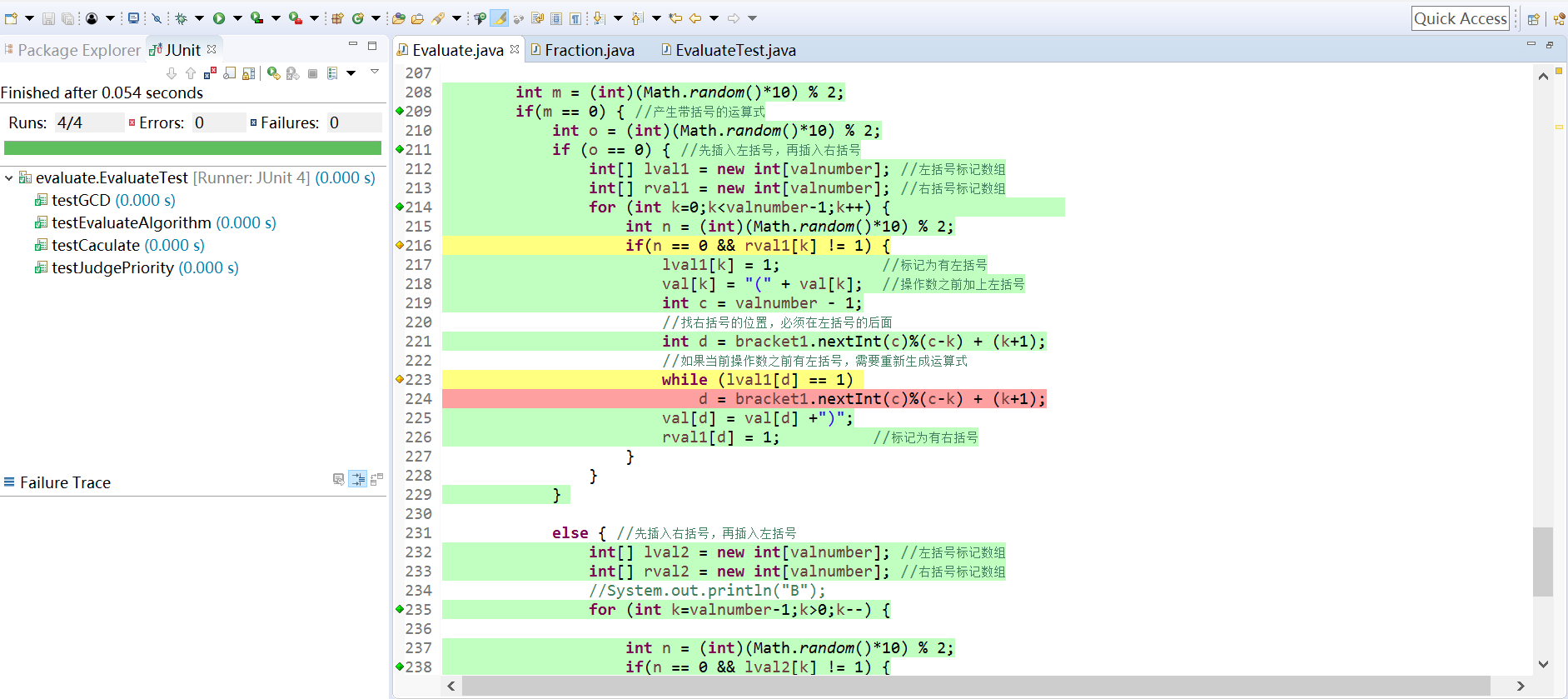
五、测试运行

---

• 单元测试（Junit）

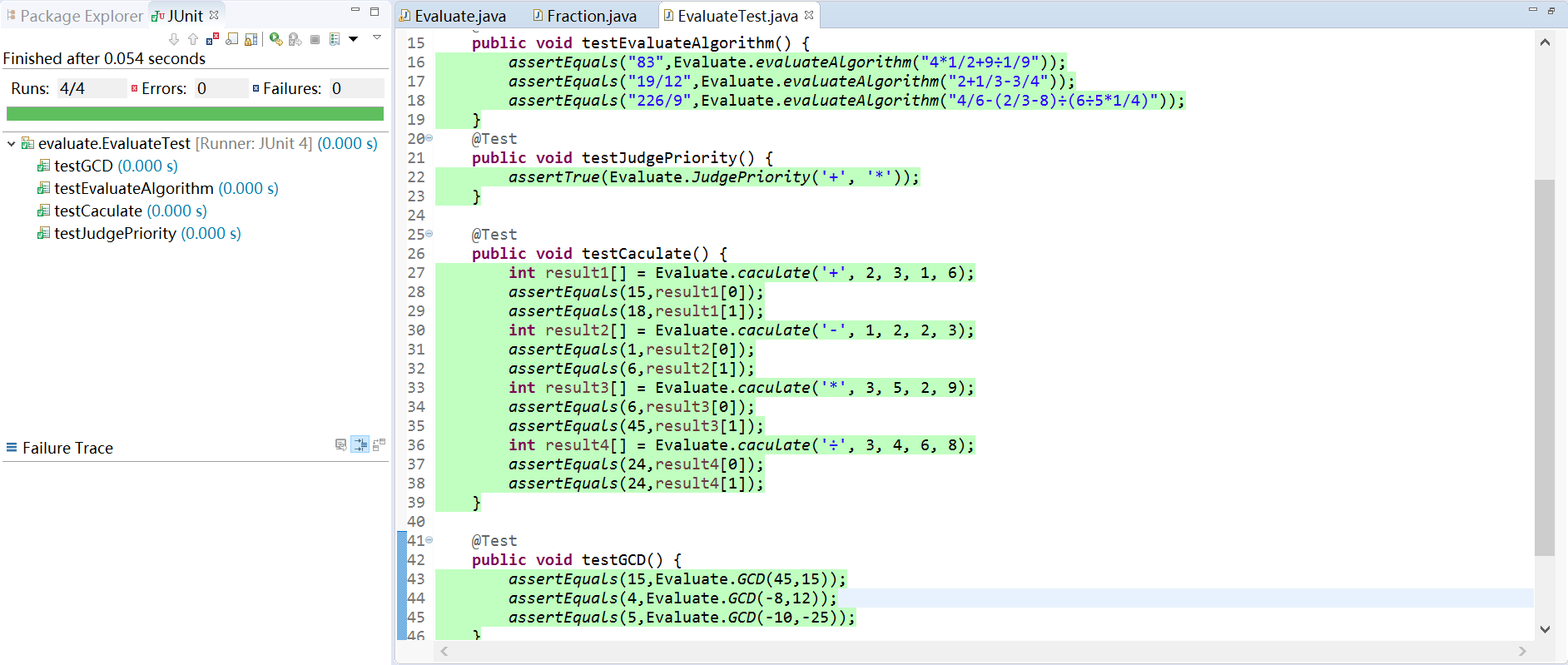
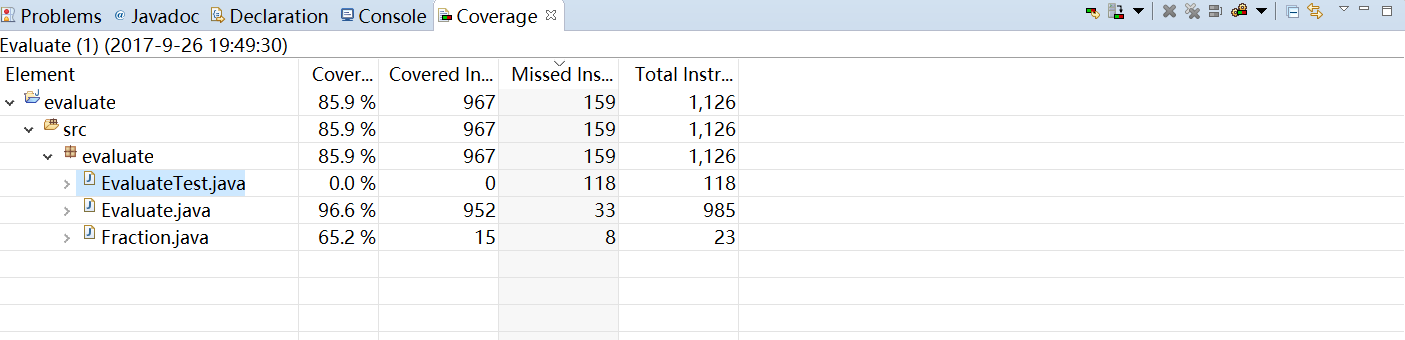
• 代码覆盖率（EclEmma插件）

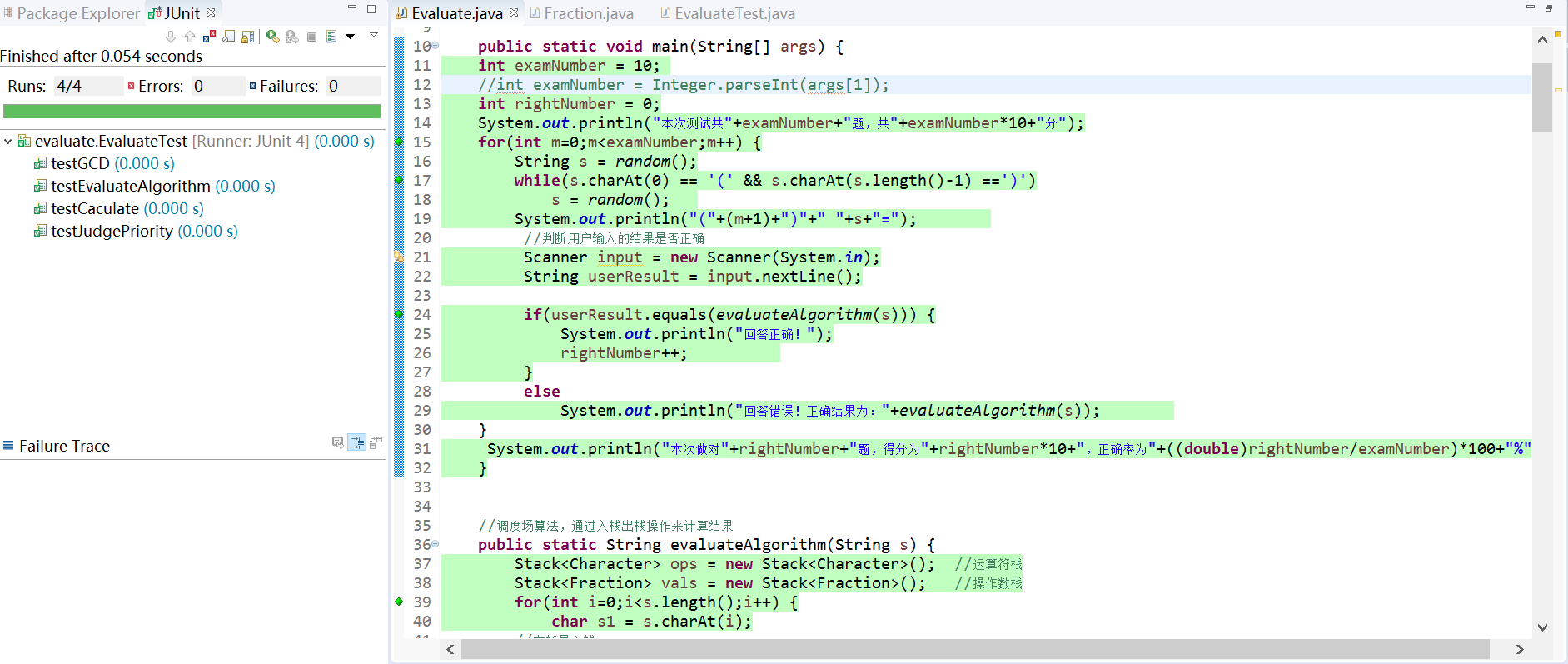
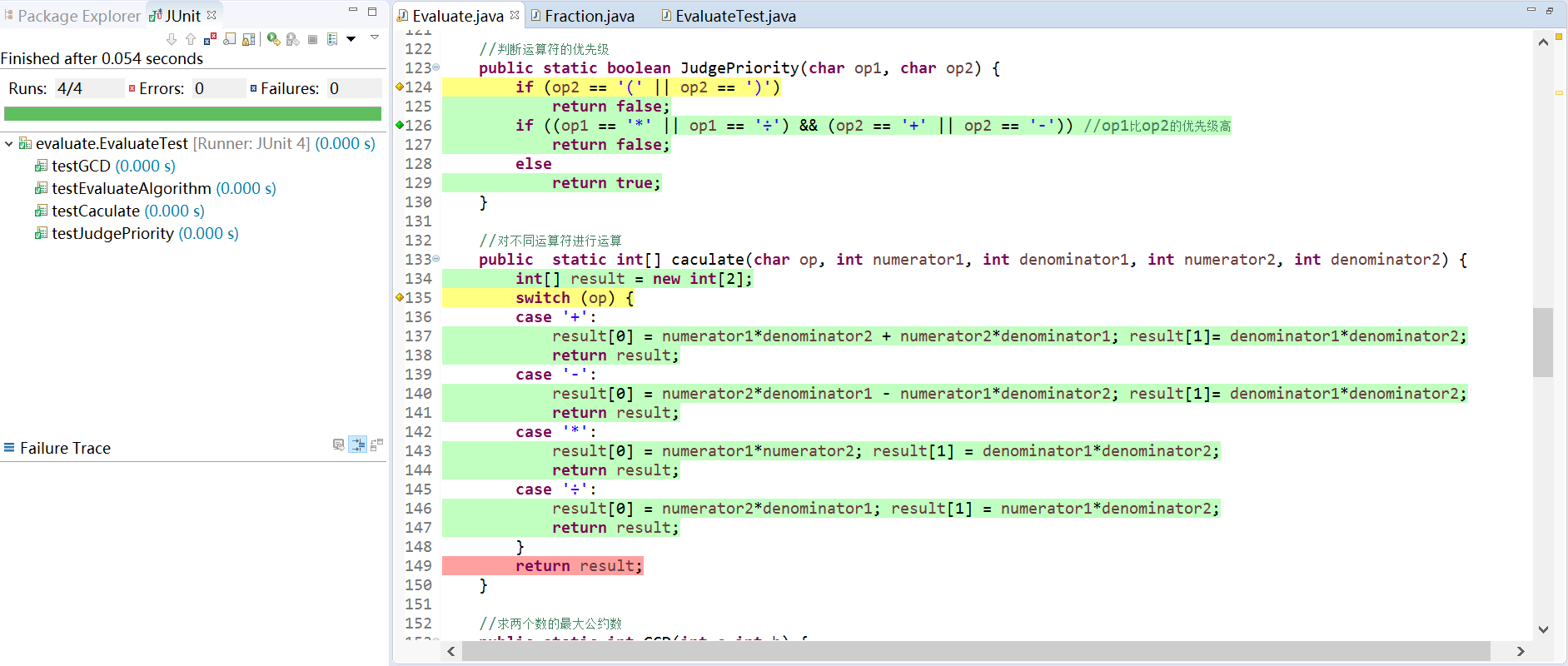
六、项目小结

---

• 寻找bug之路…任重而道远

最终的总结部分我要先把遇到的bug记录下来，在这次的项目实践中体会到无论对自己的代码怎样地信心满满，在调试过程中总会有这样那样的问题发生，有时一个不经意的小问题会折磨到令我“怀疑人生”，可见一个优秀的程序员还是要有善于发现bug的“火眼金睛”。

1. 提示空栈异常

result = caculate(ops.pop(),vals.pop().getNumerator(),vals.pop().getDenominator(),vals.pop().getNumerator(),vals.pop().getDenominator())

原因是只顾赋值操作，没有意识到每次调用vals.pop()即为出栈，之后修改为：

Fraction a = vals.pop();
Fraction b = vals.pop();				
result = caculate(ops.pop(),a.getNumerator(),a.getDenominator(),b.getNumerator(),b.getDenominator());

2. 数组的初始化操作放到了循环中，导致之后的赋值部分没有意义，因为每次循环都会初始化数组。

• 收获：

1. 第一次使用GitHub对项目做版本控制，相信之后会更加熟练地使用它。
2. 通过对《构建之法》第二章的学习，我对个人软件开发流程(PSP)有了全面的认识，并且了解到测试的重要性，本项目中我学会使用Junit，EclEmma插件对代码进行测试，对代码的执行过程更加了解。
3. 学习到java命令行参数的使用。

• 不足：

1. 在测试方面仍有不足，本项目中没有用到效能测试方法，在以后的学习过程中会逐步改进。
2. 对一些问题考虑不够全面，并且通过PSP表格也可看出对项目各方面的时间估计也有很大的偏差。

PS: 最后要特别感谢编程互助小组的D同学，不厌其烦地为我解答问题，从他身上我学到了很多:D。