人脸对齐SDM原理----Supervised Descent Method and its Applications to Face Alignment

    最近组里研究了SDM算法在人脸对齐中的应用，是CMU的论文《Supervised Descent Method and its Applications to Face Alignment》。因为思路简洁巧妙有效，两年下来引用率就有283+了，以后估计1k+，这么有影响力的文章是要学习学习。网上有了相关的原理介绍，例如：http://www.thinkface.cn/thread-2913-1-1.html。自己看了有所了解，但不能真正理解原理思路，还是直接看论文为妥。

1、问题

　　最小二乘问题中，用牛顿法求解是常用的办法，但用在求解计算机视觉的问题的时候，会遇到一些问题，比如1）、Hessian矩阵最优在局部最优的时候才是正定的，其他地方可能就不是正定的了，这就意味着求解出来的梯度方向未必是下降的方向；2）、牛顿法要求目标函数是二次可微的，但实际中未必就一定能达到要求的了；3）、Hessian矩阵会特别的大，比如人脸对其中有66个特征点，每个特征点有128维度，那么展成的向量就能达到66x128= 8448，从而Hessian矩阵就能达到8448x8448，如此大维度的逆矩阵求解，是计算量特别大的（O(p^3)次的操作和O(p^2)的存储空间）。因此避免掉Hessian矩阵的计算，Hessian不正定问题，大存储空间和计算量，寻找这样一种方法是这篇论文要解决的问题。

2、原理

    大家都知道，梯度下降法的关键是找到梯度方向和步长，对于计算机视觉问题，牛顿法求解未必能常常达到好的下降方向和步长，如下图所示：

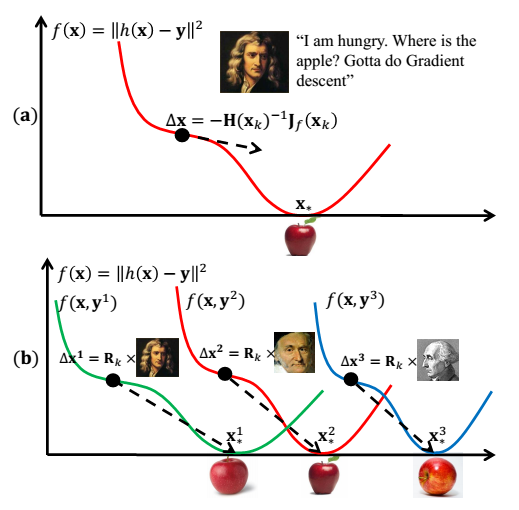
（a）为牛顿法的下降量，收敛不能达到最理想的步长和方向。而（b）本文的SDM算法，对于不同的正面侧面等情况都能得到很好的收敛方向和步长。既然Hessian矩阵的计算那么可恶，我们就直接计算梯度下降方向和步长嘛。

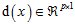    在开始讨论之前，为方便讨论，我们需要问题形式化，假设给定一张要测试的图片（这里把图像自左向右自上而下地展成了一维的向量，具有m个像素），表示图像中的p个标记点，这篇文章里面有66个标记点，如下图黑人肖像所示。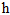表示一个非线性特征提取函数，例如 SIFT，那么。

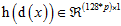    在训练阶段，已经知道了每张训练图片的真实的66个标记点，把这些点看做了是GroundTrue即参考点，如下图（a）所示。在测试的场景中，会用一个检测器把人脸检测出来，然后给一个初始化的平均标记点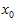，如下图（b）所示：

    那么人脸对齐问题是需要寻找一个梯度方向步长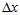，使得下面的目标函数误差最小：

    其中是人工标定的66个标记点的SIFT特征向量，在训练阶段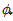和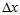都是知道的。

    好了，用牛顿法求解上述问题，其迭代的公式为：

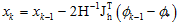
    其中，H和J分别表示Hessian矩阵和雅克比矩阵。它可以被进一步的拆分为下面的迭代公式：

    注意到，既然H和J难求，那就直接求它们的乘积，即可，于是上述的迭代公式又可以变为：

    其中和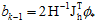，这样就转化为了之求解和的问题。接下来就是怎么求解这两个参数的问题了。

    思路很简单，就是用训练数据告诉算法下一步该往哪里走，即用当前（及之前）的迭代误差之和最小化，该问题也是一个最优化问题。如下公式所示：

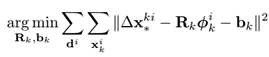
    d_i表示第i张训练图片，xki表示第i张图片在第k次迭代后的标记点的位置。实际中这样的迭代4-5次即可得到最优解，用贪心法求解。

    至此，根据以上描述的迭代步骤，即可不断地寻找到最优的人脸对齐拟合位置。SDM的流程图如下所示：

 

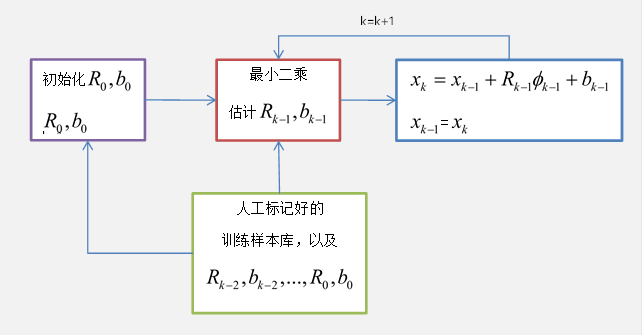
3、实验结果

    a、真实结果和拟合结果比较图：

    SDM接近于真实的标记结果，拟合结果很好。（红色的为Ground True，绿色的为SDM拟合结果）

 

    b、SDM 和 Netown的迭代收敛比较图：

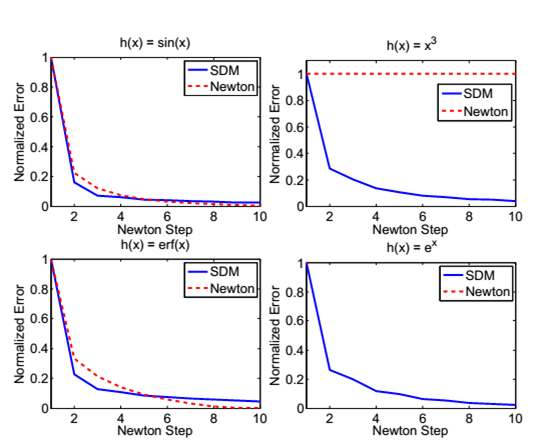
    牛顿迭代法出现迭代失败的情况，而SDM均可以迭代至收敛。

 

    c、LFPW数据集合的效果比较图：

    对灰度，戴眼镜，侧脸和遮挡都有很好的拟合效果。

 

    d、指定跟踪算法和SDM比较图：

    指定跟踪器会出现过拟合的现象，而SDM表现则相当的稳定

 

4、参考资料

    [1].http://www.thinkface.cn/thread-2913-1-1.html

    [2].Supervised Descent Method and its Applications to Face Alignment.pdf

    [3].SDM的项目的官方网址

5、源码

    下载网址：SDM(C++)，SDM(Matlab)