Dijkstra 算法

什么叫最短路径？
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径。

求最短路径的方法：

• 迪杰斯特拉算法（Dijkstra算法）
• 弗洛伊德算法（Floyd算法）
• SPFA算法

 

下面我们先来介绍一下Dijkstra算法：

Dijkstra算法

1.算法特点：

迪迦斯特拉算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

注意该算法要求图中不存在负权边。

为什么不能有负权边？

 

dijkstra由于是贪心的，每次都找一个距源点最近的点（dmin），然后将该距离定为这个点到源点的最短路径（d[i]<--dmin）；但如果存在负权边，那就有可能先通过并不是距
源点最近的一个次优点（dmin'），再通过这个负权边L(L<0)，使得路径之和更小（dmin'+L<dmin）,则dmin'+L成为最短路径，并不是dmin，

 

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

 以下例子以及代码来自于：http://www.wutianqi.com/?p=1890

例如，对下图中的有向图，应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

Dijkstra算法的迭代过程：

代码实现如下：

/***************************************
* About:    有向图的Dijkstra算法实现
* Author:   Tanky Woo
* Blog:     www.WuTianQi.com
***************************************/
 
#include <iostream>
using namespace std;
 
const int maxnum = 100;
const int maxint = 999999;
 
// 各数组都从下标1开始
int dist[maxnum];     // 表示当前点到源点的最短路径长度
int sprev[maxnum];     // 记录当前点的前一个结点
int c[maxnum][maxnum];   // 记录图的两点间路径长度
int n, line;             // 图的结点数和路径数
 
// n -- n nodes
// v -- the source node
// dist[] -- the distance from the ith node to the source node
// prev[] -- the previous node of the ith node
// c[][] -- every two nodes' distance
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
    bool s[maxnum];    // 判断是否已存入该点到S集合中
    for(int i=1; i<=n; ++i)
    {
        dist[i] = c[v][i];
        s[i] = 0;     // 初始都未用过该点
        if(dist[i] == maxint)
            sprev[i] = 0;
        else
            sprev[i] = v;
    }
    dist[v] = 0;
    s[v] = 1;
 
    // 依次将未放入S集合的结点中，取dist[]最小值的结点，放入结合S中
    // 一旦S包含了所有V中顶点，dist就记录了从源点到所有其他顶点之间的最短路径长度
         // 注意是从第二个节点开始，第一个为源点
    for(int i=2; i<=n; ++i)
    {
        int tmp = maxint;
        int u = v;
        // 找出当前未使用的点j的dist[j]最小值
        for(int j=1; j<=n; ++j)
            if((!s[j]) && dist[j]<tmp)
            {
                u = j;              // u保存当前邻接点中距离最小的点的号码
                tmp = dist[j];
            }
        s[u] = 1;    // 表示u点已存入S集合中
 
        // 更新dist
        for(int j=1; j<=n; ++j)
            if((!s[j]) && c[u][j]<maxint)
            {
                int newdist = dist[u] + c[u][j];
                if(newdist < dist[j])
                {
                    dist[j] = newdist;
                    sprev[j] = u;
                }
            }
    }
}
 
// 查找从源点v到终点u的路径，并输出
void searchPath(int *sprev,int v, int u)
{
    int que[maxnum];
    int tot = 1;
    que[tot] = u;
    tot++;
    int tmp = sprev[u];
    while(tmp != v)
    {
        que[tot] = tmp;
        tot++;
        tmp = sprev[tmp];
    }
    que[tot] = v;
    for(int i=tot; i>=1; --i)
        if(i != 1)
            cout << que[i] << " -> ";
        else
            cout << que[i] << endl;
}
 
int main()
{
    //freopen("input.txt", "r", stdin);
    // 各数组都从下标1开始
 
    // 输入结点数
    cin >> n;
    // 输入路径数
    cin >> line;
    int p, q, len;          // 输入p, q两点及其路径长度
 
    // 初始化c[][]为maxint
    for(int i=1; i<=n; ++i)
        for(int j=1; j<=n; ++j)
            c[i][j] = maxint;
 
    for(int i=1; i<=line; ++i)  
    {
        cin >> p >> q >> len;
        if(len < c[p][q])       // 有重边
        {
            c[p][q] = len;      // p指向q
            c[q][p] = len;      // q指向p，这样表示无向图
        }
    }
 
    for(int i=1; i<=n; ++i)
        dist[i] = maxint;
    for(int i=1; i<=n; ++i)
    {
        for(int j=1; j<=n; ++j)
            printf("%8d", c[i][j]);
        printf("\n");
    }
 
    Dijkstra(n, 1, dist, sprev, c);
 
    // 最短路径长度
    cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
 
    // 路径
    cout << "源点到最后一个顶点的路径为: ";
    searchPath(sprev, 1, n);
    return 0;
}

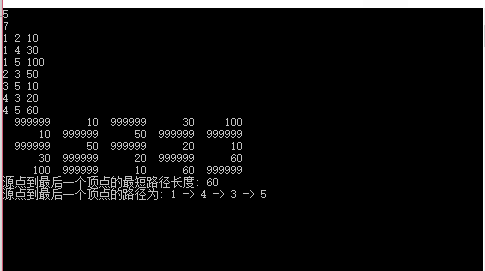
测试用例：

 

优化（用堆（优先队列）优化）

1.每次找出不包含S中最近点，加入包含s的集合

2.维护所有和这个店相连的不在包含s的集合里的点到原点的距离（Prim维护的是到包含S的集合的距离）

时间复杂度Θ（n^2）比较优，适合稠密图。

但我们发现每次找一个最近点有点耗时，因为要支持减值和求最小的操作，就用优先队列啦

（优先队列在小根堆情况下支持降值，大根堆下支持升值）但优先队列里的元素有O（E）个开空间时需注意

具体代码可以见：http://www.cnblogs.com/curo0119/p/8516550.html

参考资料：

http://www.wutianqi.com/?p=1890

http://blog.csdn.net/qq_35644234/article/details/60870719