经典排序算法学习笔记六——归并排序

归并排序

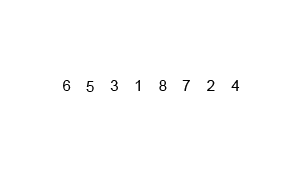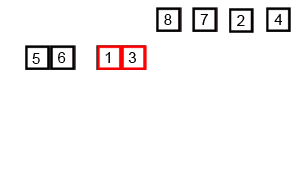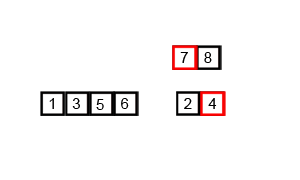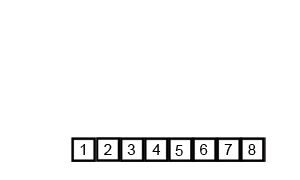
数据结构	数组
最差时间复杂度	O(n*log n)
最优时间复杂度	O(n*log n)
平均时间复杂度	O(n*log n)
最差空间复杂度	О(n)

 

 

 

 

 

1、算法思想

归并排序包括两个步骤，分别为：

第一，分解：分解待排序的n个元素的序列成各具n/2个元素的子序列；

第二，合并：合并两个已排序的子序列——这是核心部分！

递归版原理如下（假设序列共有n个元素）：

1. 将序列每相邻两个数字进行归并操作，形成floor(n/2)个序列，排序后每个序列包含两个元素
2. 将上述序列再次归并，形成floor(n/4)个序列，每个序列包含四个元素
3. 重复步骤2，直到所有元素排序完毕

2、伪代码

我是栗子，栗子，栗子

1	2	3	8	5	7	6	4	10	Merge4
1	2	3	8	5	7	6	4	10	Merge5
1	2	3	8	5	7	6	4	10	Merge2
1	2	3	8	5	7	6	4	10	Merge6
1	2	3	8	5	7	6	4	10	Merge8
1	2	3	8	5	7	4	6	10	Merge7
1	2	3	8	4	5	6	7	10	Merge3
1	2	3	4	5	6	7	8	10	Merge1

 

3、实现

 （递归版）

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

维基百科上还给出了（迭代版）https://zh.wikipedia.org/wiki/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F#.E8.BF.AD.E4.BB.A3.E6.B3.95

原理如下：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针到达序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

实现：

int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int* a = arr;
    int* b = (int*) malloc(len * sizeof(int*));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int* temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

 4、算法复杂度分析

1. 归并排序的最好、最坏和平均时间复杂度都是O(n*logn)，而空间复杂度是O(n)，比较次数介于(n*logn)/2和(n*logn)-n+1，赋值操作的次数是(2*n*logn)。

   因此，归并排序算法比较占用内存，但却是效率高且稳定的排序算法。

2. “虽然归并排序的运行时间是O(n*logn),但是它很难用于主存排序，主要问题在于合并两个排序的表需要线性附加内存，在整个算法中还要花费将数据复制到临时数组再复制回来这样一些附加的工作，其结果是严重减慢了排序的速度。

   与其他的O(n*logn)排序相比，归并排序的运行时间很大程度上依赖于在数组中进行元素的比较和移动所消耗的时间。这些消耗是和编程语言相关的。

   （1）例如，在其他语言（如Java）中，当排序一般的对象时，元素的比较耗时很多，但是移动元素就快的多。在所有流行的排序算法中，归并排序使用最少次数的比较。因此，在java中，归并排序是一般目的排序的最佳选择。事实上，在标准Java库中的一般排序就是用的这种算法。

   （2）另一方面，在C++中，对于一般排序，当对象很大时，复制对象的代价是很大的，而对象的比较通常相对消耗小些。这是因为编译器在处理函数模板的模板时具有强大的执行在线优化的能力。”——引用自vincently的博客http://www.cnblogs.com/vincently/p/4525477.html