Matrix矩阵的图像处理
矩阵的规则:
矩阵A与矩阵B能进行乘法操作的条件:
- 当矩阵A的列数等于矩阵B的行数时,A与B可以相乘。
- 矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
- 乘积C的第 i 行第 j 列的元素C ij等于矩阵A的第 i 行的元素与矩阵B的第 j 列对应元素乘积之和。
例如:

矩阵计算与各种图像变换联系
一、 平移变换
假定有一个点的坐标是 ,将其移动到
,将其移动到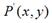 ,再假定在x轴和y轴方向移动的大小分别为:
,再假定在x轴和y轴方向移动的大小分别为:
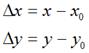
如下图所示:
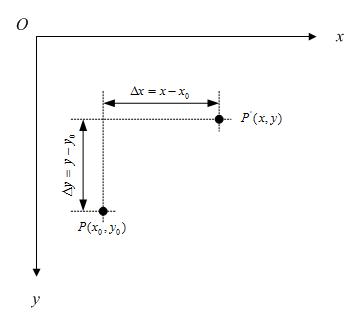
不难知道:
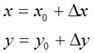
如果用矩阵来表示的话,就可以写成:
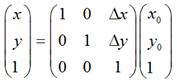
二、 旋转变换
2.1 围绕坐标原点旋转:
假定有一个点 ,相对坐标原点顺时针旋转
,相对坐标原点顺时针旋转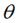 后的情形,同时假定P点离坐标原点的距离为r,如下图:
后的情形,同时假定P点离坐标原点的距离为r,如下图:
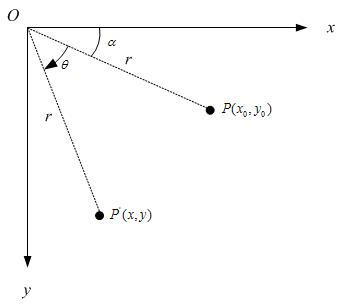
那么,
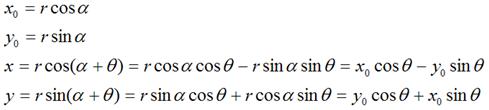
如果用矩阵,就可以表示为:
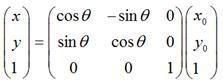
2.2 围绕某个点旋转
如果是围绕某个点 顺时针旋转
顺时针旋转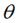 ,那么可以用矩阵表示为:
,那么可以用矩阵表示为:
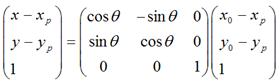
可以化为:
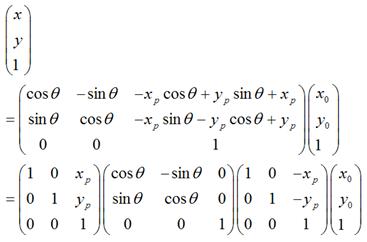
很显然,
1.
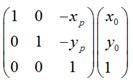 是将坐标原点移动到点
是将坐标原点移动到点 后,
后, 的新坐标。
的新坐标。
2.
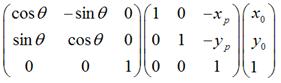
是将上一步变换后的 ,围绕新的坐标原点顺时针旋转
,围绕新的坐标原点顺时针旋转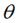 。
。
3.
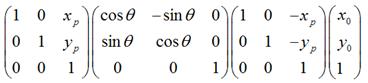
经过上一步旋转变换后,再将坐标原点移回到原来的坐标原点。
所以,围绕某一点进行旋转变换,可以分成3个步骤,即首先将坐标原点移至该点,然后围绕新的坐标原点进行旋转变换,再然后将坐标原点移回到原先的坐标原点。
三、 缩放变换
理论上而言,一个点是不存在什么缩放变换的,但考虑到所有图像都是由点组成,因此,如果图像在x轴和y轴方向分别放大k1和k2倍的话,那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍,即
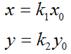
用矩阵表示就是:

如果想让它基于图片中心缩放,应该该怎么办?我们上一篇文章也说过了,要用到组合变换,
1)先将图片由中心平移到原点,这是应用变换 T
2)对图应用缩放变换 S
3)再将图片平移回到中心,应用变换 -T
下面给出它们的组合变换的公式:
四、 错切变换
错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并),它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变,而对应的y坐标(或者x坐标)则按比例发生平移,且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换,属于等面积变换,即一个形状在错切变换的前后,其面积是相等的。
比如下图,各点的y坐标保持不变,但其x坐标则按比例发生了平移。这种情况将水平错切。
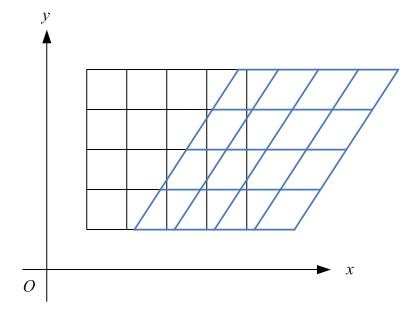
下图各点的x坐标保持不变,但其y坐标则按比例发生了平移。这种情况叫垂直错切。
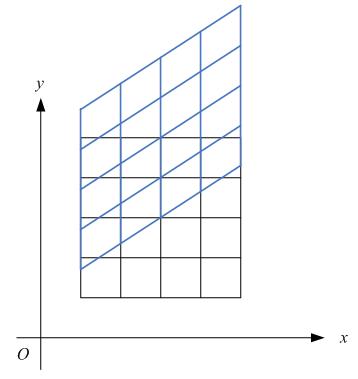
假定一个点 经过错切变换后得到
经过错切变换后得到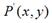 ,对于水平错切而言,应该有如下关系:
,对于水平错切而言,应该有如下关系:
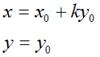
用矩阵表示就是:
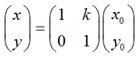
扩展到3 x 3的矩阵就是下面这样的形式:
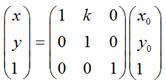
同理,对于垂直错切,可以有:
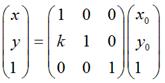
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外,还可以同时进行水平、垂直错切,那么形式上就是:

五、 对称变换
除了上面讲到的4中基本变换外,事实上,我们还可以利用Matrix,进行对称变换。所谓对称变换,就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如,某点 经过对称变换后得到
经过对称变换后得到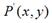 ,
,
如果对称轴是x轴,难么,
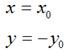
用矩阵表示就是:
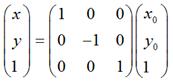
如果对称轴是y轴,那么,
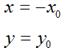
用矩阵表示就是:
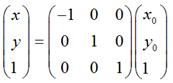
如果对称轴是y = x,如图:
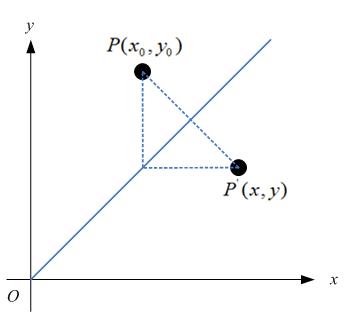
那么,
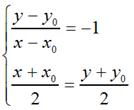
很容易可以解得:
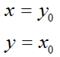
用矩阵表示就是:
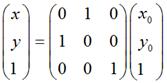
同样的道理,如果对称轴是y = -x,那么用矩阵表示就是:
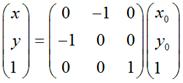
特殊地,如果对称轴是y = kx,如下图:
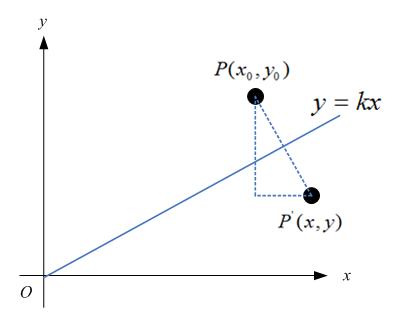
那么,
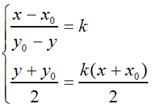
很容易可解得:
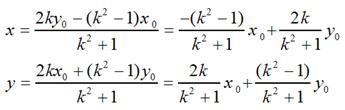
用矩阵表示就是:
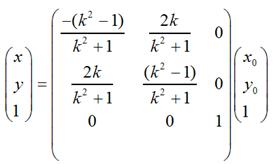
当k = 0时,即y = 0,也就是对称轴为x轴的情况;当k趋于无穷大时,即x = 0,也就是对称轴为y轴的情况;当k =1时,即y = x,也就是对称轴为y = x的情况;当k = -1时,即y = -x,也就是对称轴为y = -x的情况。不难验证,这和我们前面说到的4中具体情况是相吻合的。
如果对称轴是y = kx + b这样的情况,只需要在上面的基础上增加两次平移变换即可,即先将坐标原点移动到(0, b),然后做上面的关于y = kx的对称变换,再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的:
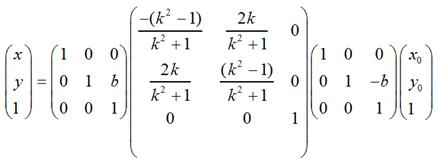
需要特别注意:在实际编程中,我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的,所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西,反之亦然。也就是说,如果要使图片在屏幕上看起来像按照数学意义上y = x对称,那么需使用这种转换:
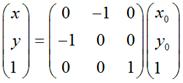
要使图片在屏幕上看起来像按照数学意义上y = -x对称,那么需使用这种转换: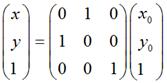
关于对称轴为y = kx 或y = kx + b的情况,同样需要考虑这方面的问题。
各种图形变换与android的Matrix联系
- 变换:默认时,这四种变换都是围绕(0,0)点变换的,当然可以自定义围绕的中心点,通常围绕中心点。
- Translate,平移变换
- Scale,缩放变换
- Rotate,旋转变换
- Skew,错切变换
- 对于每一种变换都提供了三种操作:
- set(设置Matrix的值)
- post(后乘,以
为自己,把自己从另一个矩阵的右边相乘)
- pre(先乘,以
为自己,把自己从另一个矩阵的左边相乘)
- 由上矩阵解析可得左中右分别scale(缩放),rotation(旋转)和 translation(平移)在Android中的矩阵表示:
参考api:
/** * Postconcats the matrix with the specified translation. * M' = T(dx, dy) * M */ public boolean postTranslate(float dx, float dy) { return native_postTranslate(native_instance, dx, dy); }
Matrix中set、pre、post运算顺序
1、setScale(sx,sy),首先会将该Matrix设置为对角矩阵,即相当于调用reset()方法,然后在设置该Matrix的MSCALE_X和MSCALE_Y直接设置为sx,sy的值
2、preScale(sx,sy),不会重置Matrix,而是直接与Matrix之前的MSCALE_X和MSCALE_Y值结合起来(相乘),M' = M * S(sx, sy)。
3、postScale(sx,sy),不会重置Matrix,而是直接与Matrix之前的MSCALE_X和MSCALE_Y值结合起来(相乘),M' = S(sx, sy) * M。
Matrix matrix = new Matrix(); float[] points = new float[] { 10.0f, 10.0f }; matrix.postScale(2.0f, 3.0f);// 第1步 matrix.preRotate(90);// 第2步 matrix.setScale(1.4f, 2.6f);// 第3步 matrix.postTranslate(8.0f, 7.0f);// 第4步 matrix.preScale(1.5f, 2.5f);// 第5步 matrix.mapPoints(points); Log.i("test", points[0] + ""); Log.i("test", points[1] + "");
结果为点坐标依旧为为(29.0,72.0)
经过计算,可以发现,在第3步setScale之前的第1、2步根本就没有用了,直接被第3步setScale覆盖,在从第3开始执行的。顺序为2---1----3----5----4,因为2、1被覆盖了,所以没有效果,相当于直接执行3-----5----4
总结:最后可以得出结论,在对matrix该次变换之前的所有设置中,先检测有没有setScale,如果有,直接跳到setScale那一步开始执行变换,然后在倒着执行下面所有的pre...变换,在顺着执行所有post....的变换。所以在对Matrix变换设置的时候,一定要注意顺序,不同的顺序,会有不同的结果。
API分析
缩放:
public boolean postScale (float sx, float sy) public boolean postScale (float sx, float sy, float px, float py) public boolean preScale (float sx, float sy) public boolean preScale (float sx, float sy, float px, float py) public void setScale (float sx, float sy) public void setScale (float sx, float sy, float px, float py)
其中参数sx,sy分别表示x轴和y轴的拉伸变化,如果大于1,为放大,小于1为缩小,为负值则表示对称的变化(在之后的组合变化中我们会用到它来实现镜子和倒影的效果);参数px,py用于指定缩放的中心(就是bitmap上的相对位置,而非整个画布的位置。若px=bitmap.getWidth()/2就是图片的横轴中心点。就是当缩放变化后该点的位置坐标不会变),默认为(0,0)即左上角。
旋转
public boolean preRotate (float degrees) public boolean preRotate (float degrees, float px, float py) public boolean postRotate (float degrees) public boolean postRotate (float degrees, float px, float py) public void setRotate (float degrees) public void setRotate (float degrees, float px, float py)
其中参数degrees指明了旋转的角度,如果大于零则为顺时针,小于零为逆时针;参数px,py用于指定旋转的中心,默认为(0,0)即左上角。
平移:
public boolean postTranslate (float dx, float dy) public boolean preTranslate (float dx, float dy) public void setTranslate (float dx, float dy)
其中参数dx,dy表示平移的距离,dx大于零表示向右,小于零表示向左;dy大于零表示向下,小于零表示向上。
倾斜:
public boolean postSkew (float kx, float ky) public boolean postSkew (float kx, float ky, float px, float py) public boolean preSkew (float kx, float ky) public boolean preSkew (float kx, float ky, float px, float py) public void setSkew (float kx, float ky) public void setSkew (float kx, float ky, float px, float py)
点(x,y)经过skew(kx,ky,px,py)变换之后,坐标为(kx*(y-py)+px,ky*(x-px)+py),如果,px和py没有,则默认为都为0。
组合变化
1.镜像变化:对于scale变化,如果以一个负数缩放,那么会将该 图像绘制到坐标系统的负值空间。由于(0,0)点位于左上角,使用x轴上的负数会导致向左绘制图像。因此我们需要使用postTranslate方法,将图像向右移动即可实现镜像变化。
matrix.setScale(-1, 1);
matrix.postTranslate(mBitmap.getWidth(),0);
2.倒影变化:同镜像变化,我们可以在y轴上做相同的事情,就会得到倒影的效果。
matrix.postScale(1, -1);
matrix.postTranslate(0, mBitmap.getHeight());


