树状数组及二维树状数组

　　树状数组或者二叉索引树也称作Binary Indexed Tree，又叫做Fenwick树；它的查询和修改的时间复杂度都是log(n)，空间复杂度则为O(n)，这是因为树状数组通过将线性结构转化成树状结构，从而进行跳跃式扫描。通常使用在高效的计算数列的前缀和，区间和。

为什么要用树状数组

　　线段树比树状数组功能更强大,适用范围更广,但为什么我们要写树状数组呢?我们其实看中的是树状数组,常数小且写起来快捷的特点

　　我们来看一下这一张图,右侧的每一数字都代表以该点为下标的树状数组数组(下文将称为sum数组)我们首先选取sum[16]作为观察对象,那么sum[16]就是前面16个数的和(观察黑色横线长度) 那么sum[4]发生变化时,他的直系父节点sum[4]也要跟着变化,同理sum[16]也要一起变化

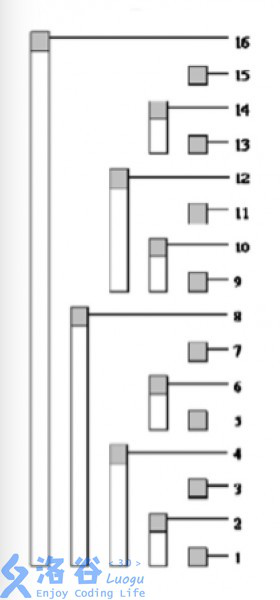
二维树状数组

　　我们来看HDU 2642这道题 那么我们略一绘画,便是这样

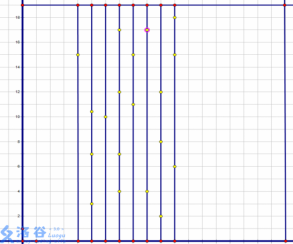
　　相信大家都知道二维差分的做法,但此题是动态的,要在过程中去维护 这时候我就产生了一种思路,就是横向做树状数组,但树状数组的每一个结点都是一棵树状数组于是 我就写出了这样的代码

　　相信大家都知道二维差分的做法,但此题是动态的,要在过程中去维护 这时候我就产生了一种思路,就是横向做树状数组,但树状数组的每一个结点都是一棵树状数组于是 我就写出了这样的代码

void update2(int p,int y,int val)
{
    for(int i=y;i<=n;i+=lowbit(i))
        sum[p][i]+=val;
}
void update1(int p,int y,int val)
{
    for(int i=p;i<=n;i+=lowbit(i))
        update2(i,y,val);
}
int query2(int p,int y)
{
    int ans=0;
    for(int i=y;i>=1;i-=lowbit(i))
        ans+=sum[p][i];
    return ans;
}
int query1(int p,int y1,int y2)
{
    int ans=0;
    for(int i=p;i>=1;i-=lowbit(i))
        ans+=(query2(i,y1)-query2(i,y2-1));
    return ans;
}

　　为了将两个query合成一个,我们换了一种query思路 将答案变换成一个大的加一个小的减两个中等的,即

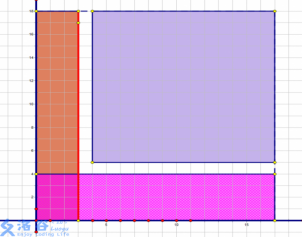
于是我们便有了这样的代码

void update(int p,int y,int val)
{
    for(int i=p;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j)) 
            sum[i][j]+=val;
}
int query(int p,int y)
{
    int ans=0;
    for(int i=p;i>=1;i-=lowbit(i))
        for(int j=y;j>=1;j-=lowbit(j))
            ans+=sum[i][j];
    return ans;
}

 总体代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <ctime>
#include <map>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
const int N=1010;
int n=1000,m,sum[N][N],book[N][N],tx1,tx2,ty1,ty2;
char a[10];
int lowbit(int x){return x&-x;}
void update(int p,int y,int val)
{
    for(int i=p;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j)) 
            sum[i][j]+=val;
}
int query(int p,int y)
{
    int ans=0;
    for(int i=p;i>=1;i-=lowbit(i))
        for(int j=y;j>=1;j-=lowbit(j))
            ans+=sum[i][j];
    return ans;
}
int main()
{
    scanf("%d",&m);
    while(m--)
    {
        scanf("%s",a);
        if(a[0]=='B')
        {
            scanf("%d%d",&tx1,&ty1);
            tx1++,ty1++;
            if(!book[tx1][ty1])
                update(tx1,ty1,1);
            book[tx1][ty1]=1; 
        }
        else if(a[0]=='D')
        {
            scanf("%d%d",&tx1,&ty1);
            tx1++,ty1++;
            if(book[tx1][ty1])
                update(tx1,ty1,-1);
            book[tx1][ty1]=0;
        }
        else
        {
            scanf("%d%d%d%d",&tx1,&tx2,&ty1,&ty2);
            tx1++,ty1++,tx2++,ty2++;
            if(tx1<tx2) swap(tx1,tx2);
            if(ty1<ty2) swap(ty1,ty2);
            printf("%d\n",query(tx1,ty1)+query(tx2-1,ty2-1)-query(tx1,ty2-1)-query(tx2-1,ty1));
        }
    }
return 0;
}
/*
5
B 581 145
B 581 145
Q 0 600 0 200
D 581 145
Q 0 600 0 200
*/