非刚性人脸跟踪 —— 面部特征检测器
本节将用一种表示方法来建立人脸特征检测器,该方法也许是人们认为最简单的模型,即:线性图像模型。由于该算法需表示一个图象块,因此这种面部特征检测器称为块模型( patch model )。该模型在 patch_model 类中被实现,该类的定义和实现可分别在 patch_model.hpp 和 patch_model.cpp 文件中找到。下面的这段代码给出了 patch_model 类的主要功能:
1 class patch_model{ //correlation-based patch expert 2 public: 3 Mat P; //normalised patch 4 ... 5 Mat //response map (CV_32F) 6 calc_response(const Mat &im, //image to compute response from 7 const bool sum2one=false); //normalize response to sum to one? 8 void 9 train(const vector<Mat> &images, //feature centered training images 10 const Size psize, //desired patch size 11 const float var = 1.0, //variance of annotation error 12 const float lambda = 1e-6, //regularization weight 13 const float mu_init = 1e-3, //initial stoch-grad step size 14 const int nsamples = 1000, //number of stoch-grad samples 15 const bool visi = false); //visualize intermediate results? 16 ... 17 };
用于检测面部特征的块模型储存在矩阵 P 中。该类有两个重要的函数: calc_response 和 train 。calc_response 函数会对搜索区域 im 的每个元素计算块模型的响应值。train 函数用来得到块模型,其大小由 psize 参数决定。
本节将介绍该类的功能。下面先来讨论相关性块(correlation patch)和它的训练过程,相关性块将被用来学习块模型。接下来介绍 patch_models 类,该类保存着每个面部特征的一些块模型,并实现了全局变换的功能。在文件 train_patch_model.cpp 和文件 visualize_patch_model.cpp 中的程序分别用来训练可视化块模型。在本节最后将简单介绍它们的用法。
一、 相关性块模型
学习检测器可用两种主要方法:生成方法(generative)和判断方法(discriminative),这两种方法的思想完全不一样。生成方法会学习一个图象块底层表示,这种表示在各种情况下都能最恰当地生成对象外观。而判断方法根据已有的对象的信息来对新对象做出最好的判断,这样已有样本来源于运行的系统。生成方法的优势在于能对具体对象的属性进行操作,可直观地查看新的对象实例的情况。著名的特征脸(Eigenface)方法就是一种流行的生成方法。判别方法的优势在于所建模型直接针对当前问题,通过已有对象来对新对象做出判别。所有判别方法中最著名的也许是支持向量机。将一个图象块作为面部特征来建模时,判别方法更好一些。
1. 学习基于判别法的块模型
给定一个标注数据集,特征检测器可从这些数据学习得到。判别块模型的学习目标是为了构造这样的图象块:当图象块与含有面部特征的图像区域交叉相关时,对特征区域有一个强的响应,而其他部分响应很弱。该模型用数学化方式可表示为:
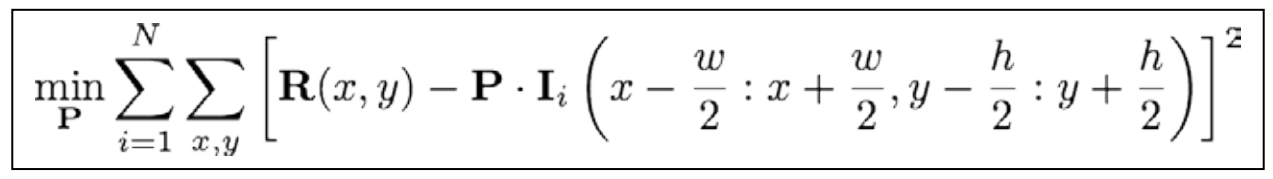
这里,P 表示块模型,Ii 表示第 i 个训练图像,Ii(a:b,c:d) 表示左上角位置和右下角位置分别是 (a,c) 和 (b,d),圆点表示内积操作,R 表示理想的响应矩阵这个目标函数的解就是一个块模型,此模型会得到一个响应矩阵,该矩阵通常在最小二乘的度量标准下最靠近理想的响应矩阵。对理想的响应矩阵 R 的一个常见选择(假定面部特征集中在训练图象块的中心)是,除中心外其他地方都设为令。在实践中,由于图像被手工标记,总会有标注误差。为了解决这个问题,通常用衰减函数来刻画 R,该函数从中心开始,随着距离增加,函数值会迅速变小。二维高斯分布可很好地充当这种函数,这也相当于假定标注误差服从高斯分布,这个过程可用下图来描述,该图为人脸左眼角外部。

上面给出的目标函数通常称为线性最小二乘,但该问题的自由度,也就是该方法的变量数与块中像素一样多,因此求解最优块模型的计算代价和所需内存会让人望而却步。
解决该问题的有效替代方法是将其看成线性方程,用随机梯度下降法来求解。该算法将团块模型的解集看成一幅地势图,通过不断迭代获得地势图梯度方向的近似估计,并每次向梯度的反方向前进,直到走到目标函数的极小值(达到阈值或迭代次数上限)。另外,随机梯度法每次随机选取样本,只需要很少的样本就能达到最优解,非常适合实时性要求较高的系统。目标函数的梯度公式为:
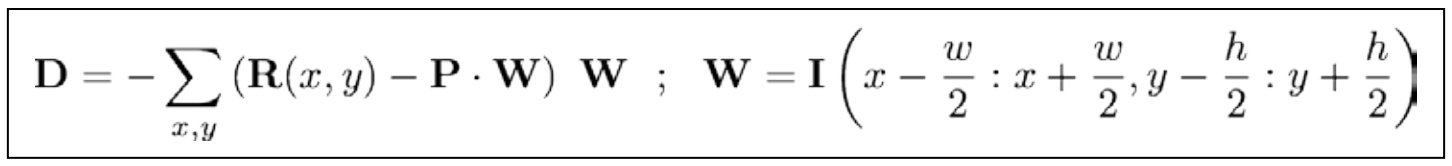
具体实现步骤:
1. 生成服从高斯分布的理想反馈图像 F
1 // 生成服从高斯分布的理想反馈图像 F 2 Size wsize = images[0].size(); 3 if((wsize.width < psize.width) || (wsize.height < psize.height)){ 4 cerr << "Invalid image size < patch size!" << endl; throw std::exception(); 5 } 6 // 设置反馈图像大小 7 int dx = wsize.width-psize.width,dy = wsize.height-psize.height; 8 Mat F(dy,dx,CV_32F); 9 for(int y = 0; y < dy; y++){ float vy = (dy-1)/2 - y; 10 for(int x = 0; x < dx; x++){ float vx = (dx-1)/2 - x; 11 // 生成函数 12 F.fl(y,x) = exp(-0.5*(vx*vx+vy*vy)/var); 13 } 14 } 15 // 归一化处理 16 normalize(F,F,0,1,NORM_MINMAX);
2. 随机梯度法求最优的团块模型
1 // 利用随机梯度下降法求最优团块模型 2 RNG rn(getTickCount()); 3 // 给定初始更新速率 4 double mu=mu_init,step=pow(1e-8/mu_init,1.0/nsamples); 5 for(int sample = 0; sample < nsamples; sample++){ 6 int i = rn.uniform(0,N); // i 为随机选中的样本图像标记 7 I = this->convert_image(images[i]); dP = 0.0; // 将图像转换为灰度图 8 for(int y = 0; y < dy; y++){ 9 for(int x = 0; x < dx; x++){ 10 Mat Wi = I(Rect(x,y,psize.width,psize.height)).clone(); 11 Wi -= Wi.dot(O); normalize(Wi,Wi); 12 // 计算目标函数的偏导数 D 13 dP += (F.fl(y,x) - P.dot(Wi))*Wi; 14 } 15 } 16 // 更新团块模型 P 17 P += mu*(dP - lambda*P); mu *= step;
学习过程完整代码 train 函数如下:

1 void 2 patch_model:: 3 train(const vector<Mat> &images, // 包含多个样本图像的矩阵向量 4 const Size psize, // 团块模型窗口的大小 5 const float var, // 手工标注错误的方差(生成理想图像时使用) 6 const float lambda, // 调整的参数(调整上一次得到的团块模型的大小) 7 const float mu_init, // 初始步长(构建梯度下降法求团块模型时的更新速率) 8 const int nsamples, // 随机选取的样本数量(梯度下降算法迭代的次数) 9 const bool visi) // 训练过程是否可观察标志 10 { 11 int N = images.size(),n = psize.width*psize.height; 12 13 // 生成服从高斯分布的理想反馈图像 F 14 Size wsize = images[0].size(); 15 if((wsize.width < psize.width) || (wsize.height < psize.height)){ 16 cerr << "Invalid image size < patch size!" << endl; throw std::exception(); 17 } 18 // 设置反馈图像大小 19 int dx = wsize.width-psize.width,dy = wsize.height-psize.height; 20 Mat F(dy,dx,CV_32F); 21 for(int y = 0; y < dy; y++){ float vy = (dy-1)/2 - y; 22 for(int x = 0; x < dx; x++){ float vx = (dx-1)/2 - x; 23 // 生成函数 24 F.fl(y,x) = exp(-0.5*(vx*vx+vy*vy)/var); 25 } 26 } 27 // 归一化处理 28 normalize(F,F,0,1,NORM_MINMAX); 29 30 //allocate memory 31 Mat I(wsize.height,wsize.width,CV_32F); // 被选中的样本灰度图像 32 Mat dP(psize.height,psize.width,CV_32F); // 目标函数的偏导数,大小同团块模型 33 Mat O = Mat::ones(psize.height,psize.width,CV_32F)/n; // 生成团块模型的归一化模板 34 P = Mat::zeros(psize.height,psize.width,CV_32F); // 团块模型 35 36 // 利用随机梯度下降法求最优团块模型 37 RNG rn(getTickCount()); 38 // 给定初始更新速率 39 double mu=mu_init,step=pow(1e-8/mu_init,1.0/nsamples); 40 for(int sample = 0; sample < nsamples; sample++){ 41 int i = rn.uniform(0,N); // i 为随机选中的样本图像标记 42 I = this->convert_image(images[i]); dP = 0.0; // 将图像转换为灰度图 43 for(int y = 0; y < dy; y++){ 44 for(int x = 0; x < dx; x++){ 45 Mat Wi = I(Rect(x,y,psize.width,psize.height)).clone(); 46 Wi -= Wi.dot(O); normalize(Wi,Wi); 47 // 计算目标函数的偏导数 D 48 dP += (F.fl(y,x) - P.dot(Wi))*Wi; 49 } 50 } 51 // 更新团块模型 P 52 P += mu*(dP - lambda*P); mu *= step; 53 if(visi){ 54 Mat R; 55 matchTemplate(I,P,R,CV_TM_CCOEFF_NORMED); // 在样本图像上寻找与团块模型匹配的区域 56 Mat PP; normalize(P,PP,0,1,NORM_MINMAX); 57 normalize(dP,dP,0,1,NORM_MINMAX); 58 normalize(R,R,0,1,NORM_MINMAX); 59 imshow("P",PP); // 归一化的团块模型 60 imshow("dP",dP); // 归一化的目标函数偏导数 61 imshow("R",R); // 与团块模型匹配的区域 62 if(waitKey(10) == 27)break; 63 } 64 }return; 65 }
二、解释全局几何变换
到目前为止,假定训练图像以面部特征进行中心化并以全局尺度和旋转进行归一化。实际上,在跟踪过程中,人脸图像随时会出现尺度或旋转变换。因此,系统必须考虑训练和测试条件之间的差异。一种方法是通过人为地在一定范围内进行尺度变换和旋转来达到我们希望的程度。但是由于联合分布团块模型的组成形式比较简单,对于手工设置的样本数据无法产生有效的响应图像response map;另一种方法,由于在一个视频中连续帧的变化相对较小,可利用前一帧对人脸所估计全局变换来对当前图像的尺度变换和旋转进行归一化处理。实现这一过程只需在学习相关块模型时选择一个参考帧即可。
patch_models 类对每个面部特征存储了相关块模型,以及训练时获得的参考帧。下面这段代码是 patch_models 类的主要功能:
1 class patch_models{ //collection of patch experts 2 public: 3 Mat reference; // 指定尺度变换和旋转的点集 4 vector<patch_model> patches; //patch models 5 ... 6 void 7 train(ft_data &data, // 存放手工标注的数据 8 const vector<Point2f> &ref, // 指定大小和旋转角度的人脸特征的参考点集 9 const Size psize, // 团块模型的大小 10 const Size ssize, // 搜索窗口的大小,即在样本图像上可以搜索团块模型的范围 11 const bool mirror = true, // use mirrored images? 12 const float var = 1.0, //variance of annotation error 13 const float lambda = 1e-6, //regularization weight 14 const float mu_init = 1e-3, //initial stoch-grad step size 15 const int nsamples = 1000, //number of stoch-grad samples 16 const bool visi = true); //visualize intermediate results? 17 18 vector<Point2f> //locations of peaks/feature 19 calc_peaks(const Mat &im, //image to detect features in 20 const vector<Point2f> &points,//initial estimate of shape 21 const Size ssize=Size(21,21));//search window size 22 ... 23 };
那么如何通过合理的几何变换让样本图像训练出最好的团块模型?我们可以参考上一篇博文中的 Procrustes 算法计算每幅样本图像中特征点集的几何结构到参考人脸模型的变换矩阵,再利用这个矩阵对样本图像进行仿射变化(缩放、旋转、偏移)。具体实现如下:
1 void 2 patch_models:: 3 train(ft_data &data, 4 const vector<Point2f> &ref, 5 const Size psize, 6 const Size ssize, 7 const bool mirror, 8 const float var, 9 const float lambda, 10 const float mu_init, 11 const int nsamples, 12 const bool visi) 13 { 14 //set reference shape 15 int n = ref.size(); reference = Mat(ref).reshape(1,2*n); 16 Size wsize = psize + ssize; // wsize 为归一化的样本图像大小 17 18 //train each patch model in turn 19 // n 个特征点将对应 n 个团块 20 patches.resize(n); 21 for(int i = 0; i < n; i++){ 22 if(visi)cout << "training patch " << i << "..." << endl; 23 vector<Mat> images(0); 24 for(int j = 0; j < data.n_images(); j++){ // 遍历所有样本图像 25 Mat im = data.get_image(j,0); 26 vector<Point2f> p = data.get_points(j,false); // 获取手工标注的样本点 27 Mat pt = Mat(p).reshape(1,2*n); 28 Mat S = this->calc_simil(pt),A(2,3,CV_32F); // 计算样本点到参考模型的变化矩阵 29 A.fl(0,0) = S.fl(0,0); A.fl(0,1) = S.fl(0,1); // 构造仿射变换矩阵 30 A.fl(1,0) = S.fl(1,0); A.fl(1,1) = S.fl(1,1); 31 A.fl(0,2) = pt.fl(2*i ) - 32 (A.fl(0,0) * (wsize.width-1)/2 + A.fl(0,1)*(wsize.height-1)/2); 33 A.fl(1,2) = pt.fl(2*i+1) - 34 (A.fl(1,0) * (wsize.width-1)/2 + A.fl(1,1)*(wsize.height-1)/2); 35 Mat I; warpAffine(im,I,A,wsize,INTER_LINEAR+WARP_INVERSE_MAP); // 对样本进行仿射变换 36 images.push_back(I); 37 if(mirror){ 38 im = data.get_image(j,1); 39 p = data.get_points(j,true); 40 pt = Mat(p).reshape(1,2*n); 41 S = this->calc_simil(pt); 42 A.fl(0,0) = S.fl(0,0); A.fl(0,1) = S.fl(0,1); 43 A.fl(1,0) = S.fl(1,0); A.fl(1,1) = S.fl(1,1); 44 A.fl(0,2) = pt.fl(2*i ) - 45 (A.fl(0,0) * (wsize.width-1)/2 + A.fl(0,1)*(wsize.height-1)/2); 46 A.fl(1,2) = pt.fl(2*i+1) - 47 (A.fl(1,0) * (wsize.width-1)/2 + A.fl(1,1)*(wsize.height-1)/2); 48 warpAffine(im,I,A,wsize,INTER_LINEAR+WARP_INVERSE_MAP); 49 images.push_back(I); 50 } 51 } 52 patches[i].train(images,psize,var,lambda,mu_init,nsamples,visi); // 从样本图像中训练团块模型 53 } 54 }
其中 calc_simil 函数用来计算仿射变换矩阵,实现过程如下:
1 Mat 2 patch_models:: 3 calc_simil(const Mat &pts) 4 { 5 //compute translation 6 int n = pts.rows/2; 7 // 计算标注点的重心 8 float mx = 0,my = 0; 9 for(int i = 0; i < n; i++){ 10 mx += pts.fl(2*i); my += pts.fl(2*i+1); 11 } 12 Mat p(2*n,1,CV_32F); mx /= n; my /= n; 13 for(int i = 0; i < n; i++){ 14 p.fl(2*i) = pts.fl(2*i) - mx; p.fl(2*i+1) = pts.fl(2*i+1) - my; 15 } 16 //compute rotation and scale 17 float a=0,b=0,c=0; 18 for(int i = 0; i < n; i++){ 19 a += reference.fl(2*i) * reference.fl(2*i ) + 20 reference.fl(2*i+1) * reference.fl(2*i+1); 21 b += reference.fl(2*i) * p.fl(2*i ) + reference.fl(2*i+1) * p.fl(2*i+1); 22 c += reference.fl(2*i) * p.fl(2*i+1) - reference.fl(2*i+1) * p.fl(2*i ); 23 } 24 b /= a; c /= a; 25 float scale = sqrt(b*b+c*c),theta = atan2(c,b); 26 float sc = scale*cos(theta),ss = scale*sin(theta); 27 // 前两列为缩放旋转,最后一列为平移 28 return (Mat_<float>(2,3) << sc,-ss,mx,ss,sc,my); 29 }
三、训练与可视化
在 train_patch_model.cpp 文件中有通过标注数据来训练块模型的示例程序。命令行 argv[1] 保存着标注数据的路径,通过它可加载数据到内存,并删除不完备样本,然后开始训练:
1 //load data 2 ft_data data = load_ft<ft_data>(argv[1]); 3 data.rm_incomplete_samples(); 4 if(data.imnames.size() == 0){ 5 cerr << "Data file does not contain any annotations."<< endl; return 0; 6 }
上一篇博客通过对数据集训练已得到一个形状模型,且将该模型储存在 argv[2] 参数所指向的路径中,可通过 argv[2] 参数来加载此模型,然后由此计算选择的 reference 形状。具体实现如下:
1 //load shape model 2 shape_model smodel = load_ft<shape_model>(argv[2]);
下面是对已缩放且被中心化后的平均形状进行计算:
1 //generate reference shape 2 smodel.p = Scalar::all(0.0); 3 smodel.p.fl(0) = calc_scale(smodel.V.col(0),width); 4 vector<Point2f> r = smodel.calc_shape();
在得到 reference 形状 r 后,可通过下面这个函数在训练块模型集合并保存:
1 //train patch models 2 patch_models pmodel; 3 pmodel.train(data,r,Size(psize,psize),Size(ssize,ssize),mirror); 4 save_ft<patch_models>(argv[3],pmodel);
运行程序可以得到训练好的块模型并保存在 patch_model.yaml 中,如下图:
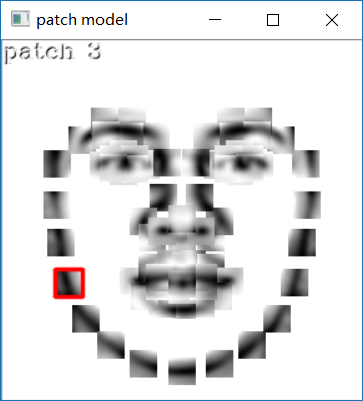
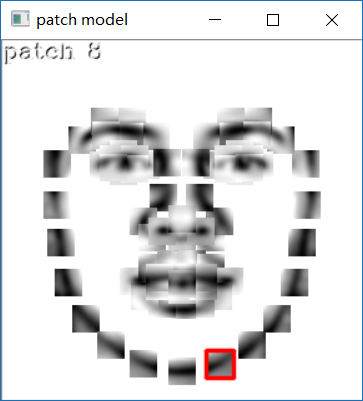
一旦训练完成,就可用文件 visualize_patch_model.cpp 中的程序对得到的块模型进行可视化操作。这个程序可得到:所有块模型的复合图像 P、参考形状中各特征所在位置的中心、reference、显示当前活动块周围有界的矩形区域。
主要代码如下:
1 // 加载团块模型 2 patch_models pmodel = load_ft<patch_models>(argv[1]); 3 4 //compute scale factor 5 float scale = calc_scale(pmodel.reference,width); 6 int height = calc_height(pmodel.reference,scale); 7 8 //compute image width 9 int max_width = 0,max_height = 0; 10 for(int i = 0; i < pmodel.n_patches(); i++){ 11 Size size = pmodel.patches[i].patch_size(); 12 max_width = max(max_width,int(scale*size.width)); 13 max_height = max(max_width,int(scale*size.height)); 14 } 15 //create reference image 16 // 将所有块模型根据标注点位置贴到同一图像上 17 Size image_size(width+4*max_width,height+4*max_height); 18 Mat image(image_size.height,image_size.width,CV_8UC3); 19 image = Scalar::all(255); 20 vector<Point> points(pmodel.n_patches()); 21 vector<Mat> P(pmodel.n_patches()); 22 for(int i = 0; i < pmodel.n_patches(); i++){ 23 Mat I1; normalize(pmodel.patches[i].P,I1,0,255,NORM_MINMAX); 24 Mat I2; resize(I1,I2,Size(scale*I1.cols,scale*I1.rows)); 25 Mat I3; I2.convertTo(I3,CV_8U); cvtColor(I3,P[i],CV_GRAY2RGB); 26 points[i] = Point(scale*pmodel.reference.fl(2*i ) + 27 image_size.width /2 - P[i].cols/2, 28 scale*pmodel.reference.fl(2*i+1) + 29 image_size.height/2 - P[i].rows/2); 30 Mat I = image(Rect(points[i].x,points[i].y,P[i].cols,P[i].rows)); 31 P[i].copyTo(I); 32 } 33 //animate 34 namedWindow("patch model"); 35 int i = 0; 36 while(1){ 37 Mat img = image.clone(); 38 Mat I = img(Rect(points[i].x,points[i].y,P[i].cols,P[i].rows)); 39 P[i].copyTo(I); 40 rectangle(img,points[i],Point(points[i].x+P[i].cols,points[i].y+P[i].rows), 41 CV_RGB(255,0,0),2,CV_AA); 42 char str[256]; sprintf(str,"patch %d",i); draw_string(img,str); 43 imshow("patch model",img); 44 int c = waitKey(0); // q 退出,p 下一个块模型,o 上一个块模型 45 if(c == 'q')break; 46 else if(c == 'p')i++; 47 else if(c == 'o')i--; 48 if(i < 0)i = 0; else if(i >= pmodel.n_patches())i = pmodel.n_patches()-1; 49 } 50 destroyWindow("patch model");
运行效果如下:
四、总结
概括一下本节团块特征提取算法都经历了哪些操作:
- 获取手工标注的样本点、样本图像名称、形变模型 (v,e,c)
- 指定大小与旋转角度,通过形状模型的联合变化矩阵 v,生成人脸特征点的参考模型 ref
- 计算每幅样本图像的标注点到参考特征点的旋转角度 S
- 利用旋转构造仿射变化矩阵,对样本图像进行仿射变换 A
- 利用随机梯度下降法对新生成的样本图像求解每个特征点对应的团块模型 patch_model




