相似性度量 - 数据挖掘算法（2）

（2017-04-03 银河统计）

相似性和相异性被许多数据挖掘技术所使用，如聚类、最近邻分类、异常检测等。不同组样本之间的相似度是样本间差异程度的数值度量，两组样本越相似，它们的相异度就越低，相似度越高。通常用各种“距离”和“相关系数”作为相异度或相似度相异度度量方法。

一、距离计算###

1、欧氏距离(Euclidean Distance)

欧氏距离是一个经常采用的距离公式，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。二维平面上两点\(A(X_1,Y_1)\)与\(B(X_2,Y_2)\)间的欧氏距离：

\[D_{12}=\sqrt{(X_1-X_2)^2+(Y_1-Y_2)^2} \]

三维空间两点\(A(X_1,Y_1,Z_1)\)与\(B(X_2,Y_2,Z_2)\)间的欧氏距离：

\[D_{12}=\sqrt{(X_1-X_2)^2+(Y_1-Y_2)^2+(Z_1-Z_2)^2} \]

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的欧氏距离：

\[D_{ij}=\sqrt{(X_{i1}-X_{j1})^2+(X_{i2}-X_{j2})^2+\dots+(X_{im}-X_{jm})^2}=\sqrt{\sum\limits_{k=1}^m(X_{ik}-X_{jk})^2} \]

现有10名学生六门课程成绩表（附表I）如下：

序号概率论统计学英语政治数据挖掘线性代数
1676373754491
2746966948155
3769393797127
4653885856145
5803948754152
6728070888643
7605091954264
8774969508955
9658950709985
10784155897128

计算第3名和第5名学生成绩之间的欧氏距离。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，两者欧氏距离为，

\[D_{35}=\sqrt{(76-80)^2+(93-39)^2+(93-48)^2+(79-75)^2+(71-41)^2+(27-52)^2}\approx 80.61 \]

欧氏距离函数代码

## 函数
    webTJ.Datamining.getOSDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oOSDis=webTJ.Datamining.getOSDis(oArr1,oArr2); 
webTJ.display("欧氏距离 = "+oOSDis,0);

运用距离公式计算所有不同组样本之间距离，即样本相似（距离）矩阵，综合反映了不同组样本之间的相似性或差异性。样本相似（距离）矩阵是分类、聚类等数据挖掘方法的基础。

欧氏距离矩阵函数代码

## 函数
    webTJ.Datamining.getOSDiss(arrs);
##参数
    【arrs,i,j】
    【二维数组,第i个向量,第j个向量】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oOSDiss=webTJ.Datamining.getOSDiss(oArrs); 
webTJ.show(oOSDiss,2);

2、曼哈顿距离(Manhattan Distance)

曼哈顿距离也称为城市街区距离(City Block distance)，想象在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是“曼哈顿距离”。

曼哈顿距离由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

可以定义曼哈顿距离为在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标\((X_1,Y_1)\)与坐标\((X_2,Y_2)\)的曼哈顿距离为：

\[D_{12}=|X_1-X_2|+|Y_1-Y_2| \]

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的曼哈顿距离：

\[D_{ij}=|X_{i1}-X_{j1}|+|X_{i2}-X_{j2}|+\dots+|X_{im}-X_{jm}|=\sum\limits_{k=1}^m|X_{ik}-X_{jk}| \]

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的曼哈顿距离。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，两者曼哈顿距离为，

\[D_{35}=|76-80|+|93-39|+|93-48|+|79-75|+|71-41|+|27-52|=162 \]

曼哈顿距离函数代码

## 函数
    webTJ.Datamining.getMHDDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oMHDDis=webTJ.Datamining.getMHDDis(oArr1,oArr2); 
webTJ.display("曼哈顿距离 = "+oMHDDis,0);

曼哈顿距离矩阵函数代码

## 函数
    webTJ.Datamining.getMHDDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oMHDDiss=webTJ.Datamining.getMHDDiss(oArrs); 
webTJ.show(oMHDDiss,2);

3、切比雪夫距离(Chebyshev Distance)

切比雪夫距离得名自俄罗斯数学家切比雪夫。在数学中，切比雪夫距离是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。例如在平面上，坐标\((X_1,Y_1)\)与坐标\((X_2,Y_2)\)的切比雪夫距离为：

\[D_{12}=max(|X_1-X_2|,|Y_1-Y_2|) \]

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的切比雪夫距离：

\[D_{ij}=max(|X_{i1}-X_{j1}|,|X_{i2}-X_{j2}|,\dots,|X_{im}-X_{jm}|) \]

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的切比雪夫距离。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，两者切比雪夫距离为，

\[D_{35}=max(|76-80|,|93-39|,|93-48|,|79-75|,|71-41|,|27-52|)=54 \]

切比雪夫距离函数代码

## 函数
    webTJ.Datamining.getCDDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oCDDis=webTJ.Datamining.getCDDis(oArr1,oArr2); 
webTJ.display("切比雪夫距离 = "+oCDDis,0);

切比雪夫距离矩阵函数代码

## 函数
    webTJ.Datamining.getCDDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oCDDiss=webTJ.Datamining.getCDDiss(oArrs); 
webTJ.show(oCDDiss,2);

4、闵氏距离(Minkowski Distance)

又叫做闵可夫斯基距离 ,是欧氏空间中的一种测度，被看做是欧氏距离的一种推广，欧氏距离是闵可夫斯基距离的一种特殊情况。例如在平面上，坐标\((X_1,Y_1)\)与坐标\((X_2,Y_2)\)的闵氏距离为：

\[D_{12}=(|X_1-X_2|^p+|Y_1-Y_2|^p)^{\frac{1}{p}} \]

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的闵氏距离：

\[D_{ij}=(|X_{i1}-X_{j1}|^p+|X_{i2}-X_{j2}|^p+\dots+|X_{im}-X_{jm}|^p)^{\frac{1}{p}}=(\sum\limits_{k=1}^m|X_{ik}-X_{jk}|^p)^{\frac{1}{p}} \]

闵氏距离不是一种距离，而是一组距离的定义。该距离最常用的p是2和1，前者是欧几里得距离，后者是曼哈顿距离。当\(p\rightarrow\infty\)时，

\[\lim_{p\to\infty}(\sum\limits_{k=1}^m|X_{ik}-X_{jk}|^p)^{\frac{1}{p}}=max(|X_{i1}-X_{j1}|,|X_{i2}-X_{j2}|,\dots,|X_{im}-X_{jm}|) \]

即\(p\rightarrow\infty\)时为切比雪夫距离。

上图反映了不同闵氏距离系数p的几何意义。

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的闵可夫斯基距离(p=1.5)。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，两者闵可夫斯基距离为，

\[\small{D_{35}=(|76-80|^{1.5}+|93-39|^{1.5}+|93-48|^{1.5}+|79-75|^{1.5}+|71-41|^{1.5}+|27-52|^{1.5})^{\frac{1}{1.5}}=100.2667} \]

闵氏距离函数代码

## 函数
    webTJ.Datamining.getMSDis(arr1,arr2,p);
##参数
    【arr1,arr2,p】
    【一维数组1,一维数组2,闵氏系数】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oP=1.5;
var oMSDis=webTJ.Datamining.getMSDis(oArr1,oArr2,oP); 
webTJ.display("闵氏距离 = "+oMSDis,0);

闵氏距离矩阵函数代码

## 函数
    webTJ.Datamining.getMSDiss(arrs,p);
##参数
    【arrs,p】
    【二维数组,闵氏系数】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oMSDiss=webTJ.Datamining.getMSDiss(oArrs,1.5); 
webTJ.show(oMSDiss,2);

5、马氏距离(Mahalanobis Distance)

马氏距离由印度统计学家马哈拉诺斯（P.C.Mahalanobis）提出，表示数据的协方差距离，与欧式距离不同，它考虑了各指标之间相关性的干扰，而且不受各指标量纲的影响，但是它的缺点是夸大了变化微小的变量的作用。

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的马氏距离：

\[D_{ij}=\sqrt{(X_i-X_j)^TS^{-1}(X_i-X_j)} \]

式中S为样本协方差，\(X_i\)和\(X_j\)为空间两点的向量。和前面的距离公式相比，马氏距离计算比较复杂，下面给出一个简单案例。

现有样本集为：{(1,2),(3,4),(4,6),(2,3),(3,5)}，求两样本{(1,2),(2,3)}的马氏距离。

解、该样本集为二维变量5组样本。协方差公式为：

\[S=\frac{1}{n-1}\times \left[ \begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix} \right] \]

当样本集为m维变量时有，

\[S=\frac{1}{n-1}\times \left[ \begin{matrix} L_{11} & L_{12} & \dots & L_{1m}\\ L_{21} & L_{22} & \dots & L_{2m}\\ \dots & \dots & \dots & \dots \\ L_{m1} & L_{m2} & \dots & L_{mm} \end{matrix} \right] \]

矩阵中，

\[L_{ii}=\sum\limits_{k=1}^n(X_{ik}-\overline{X}_{i})^2=\sum\limits_{k=1}^nX_{ik}^2-\frac{1}{n}(\sum\limits_{k=1}^nX_{ik})^2 \]

\[L_{ij}=\sum\limits_{k=1}^n(X_{ik}-\overline{X}_{i})(X_{jk}-\overline{X}_{j})=\sum\limits_{k=1}^nX_{ik}X_{jk}-\frac{1}{n}(\sum\limits_{k=1}^nX_{ik})\times (\sum\limits_{k=1}^nX_{jk}) \]

根据样本数据计算得，

\[n=5,\sum\limits_{k=1}^5X_{1k}=13,\sum\limits_{k=1}^5X_{2k}=20,\sum\limits_{k=1}^5X_{1k}^2=39,\sum\limits_{k=1}^5X_{2k}^2=90,\sum\limits_{k=1}^5X_{1k}X_{2k}=59, \]

\[L_{11}=39-\frac{1}{5}\times 13^2=5.2,L_{22}=90-\frac{1}{5}\times 20^2=10,L_{12}=L_{21}=59-\frac{1}{5}\times 13\frac 20=7 \]

\[S=\frac{1}{n-1}\times \left[ \begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix} \right]= \frac{1}{5-1}\times \left[ \begin{matrix} 5.2 & 7 \\ 7 & 10 \end{matrix} \right]= \left[ \begin{matrix} 1.3 & 1.75 \\ 1.75 & 2.5 \end{matrix} \right] \]

\[S= \left[ \begin{matrix} 1.3 & 1.75 \\ 1.75 & 2.5 \end{matrix} \right]^{-1}= \left[ \begin{matrix} 13.3333 & -9.3333 \\ -9.3333 & 9.9333 \end{matrix} \right] \]

\[D_{ij}=\sqrt{(X_i-X_j)^TS^{-1}(X_i-X_j)} =(\left[ \begin{matrix} 2 - 1 \\ 3 - 2 \end{matrix} \right]^T\times \left[ \begin{matrix} 13.3333 & -9.3333 \\ -9.3333 & 9.9333 \end{matrix} \right]\times \left[ \begin{matrix} 2 - 1 \\ 3 - 2 \end{matrix} \right])^{\frac{1}{2}} \]

\[=(\left[ \begin{matrix} 1 \\ 1 \end{matrix} \right]^T\times \left[ \begin{matrix} 13.3333 & -9.3333 \\ -9.3333 & 9.9333 \end{matrix} \right]\times \left[ \begin{matrix} 1 \\ 1 \end{matrix} \right])^{\frac{1}{2}} =1.6^{\frac{1}{2}}=1.264911 \]

马氏距离函数代码

## 函数
    webTJ.Datamining.getMAHDis(arr1,arr2,arrs);
##参数
    【arr1,arr2,arrs】
    【一维数组1,一维数组2,二维数组】

代码样例

webTJ.clear();
var oSrrs=[[1,2],[3,4],[4,6],[2,3],[3,5]];
var oArr1=[1,2];
var oArr2=[2,3];
var oMAHDis=webTJ.Datamining.getMAHDis(oArr1,oArr2,oSrrs);
webTJ.display("马氏距离 = "+oMAHDis,0);
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
oArr1=[76,93,93,79,71,27];
oArr2=[80,39,48,75,41,52];   
oMAHDis=webTJ.Datamining.getMAHDis(oArr1,oArr2,oArrs); 
webTJ.display("马氏距离 = "+oMAHDis,0);

马氏距离矩阵函数代码

## 函数
    webTJ.Datamining.getMAHDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oSrrs=[[1,2],[3,4],[4,6],[2,3],[3,5]];
var oMAHDiss=webTJ.Datamining.getMAHDiss(oSrrs);
webTJ.show(oMAHDiss,2);
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oMAHDiss=webTJ.Datamining.getMAHDiss(oArrs); 
webTJ.show(oMAHDiss,2);

二、相似系数计算###

1、皮尔逊相关系数(Pearson Correlation coefficient)

皮尔逊相关系数也称为简单相关系数，在统计学中，皮尔逊相关系数用于度量两个变量X和Y之间的相关（线性相关）程度，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高，负值表示负相关，正值表示正相关。在自然、社会科学领域中，该系数广泛用于度量两个变量之间的相关程度。

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的相关系数公式为：

\[R_{ij}=\frac{\sum\limits_{k=1}^n(X_{ik}-\overline{X}_i)(X_{jk}-\overline{X}_j)}{\sqrt{(X_{ik}-\overline{X}_i)^2}\sqrt{(X_{jk}-\overline{X}_j)^2}}=\frac{\sum\limits X_{i}X_{j}-\frac{\sum\limits X_{i}\sum\limits X_{j}}{n}}{\sqrt{\sum\limits X_{i}^2-\frac{(\sum\limits X_{i})^2}{n}}\sqrt{\sum\limits X_{j}^2-\frac{(\sum\limits X_{j})^2}{n}}}=\frac{L_{ij}}{\sqrt{L_{ii}L_{jj}}} \]

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的曼哈顿距离。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，皮尔逊相关系数，

\[L_{33}=\sum\limits_{k=1}^mX_{3k}^2-\frac{1}{m}(\sum\limits_{k=1}^mX_{3k})^2=35085-\frac{1}{6}439^2=2964.8333 \]

\[L_{55}=\sum\limits_{k=1}^mX_{5k}^2-\frac{1}{m}(\sum\limits_{k=1}^mX_{5k})^2=20235-\frac{1}{6}335^2=1530.8333 \]

\[L_{35}=\sum\limits_{k=1}^mX_{3k}X_{5k}-\frac{1}{m}(\sum\limits_{k=1}^mX_{3k})(\sum\limits_{k=1}^mX_{5k})=24411-\frac{1}{6}439\times 335=-99.8333 \]

\[R_{35}=\frac{L_{35}}{\sqrt{L_{33}L_{55}}}=\frac{-99.8333}{\sqrt{2964.8333\times 1530.8333}}=-0.04686 \]

皮尔逊相关系数函数代码

## 函数
    webTJ.Datamining.getCORDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();    
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oCORDis=webTJ.Datamining.getCORDis(oArr1,oArr2); 
webTJ.display("皮尔逊相关系数 = "+oCORDis,0);

皮尔逊相关系数矩阵函数代码

## 函数
    webTJ.Datamining.getMAHDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oCORDiss=webTJ.Datamining.getCORDiss(oArrs); 
webTJ.show(oCORDiss,2);

2、斯皮尔曼秩相关系数（Spearman Rank Correlation）

斯皮尔曼秩相关系数又称为斯皮尔曼等级相关（Spearman's correlation coefficient for ranked data）。主要用于解决顺序数据相关的问题。适用于两列变量，而且具有等级变量性质具有线性关系的资料。由英国心理学家、统计学家斯皮尔曼根据积差相关的概念推导而来。斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的等级相关\(\rho\)可以达到+1或-1。

斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关系数来进行研究。

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的斯皮尔曼秩相关系数公式：

\[\rho=1-\frac{6\sum\limits_{k=1}^m{d_k^2}}{n(n^2-1)} \]

式中\(d\)为\(X_{i}\)、\(X_{j}\)的秩次差平方。

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的斯皮尔曼秩相关系数。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，斯皮尔曼秩相关系数计算表如下：

位置原始A原始B秩次A秩次B秩次差平方d
17680419
293391625
39348244
47975321
57141550
62752639
合计48

注：将向量A从大到小排序，排序后向量A中的76其序位为4，即秩次为4。向量A中有2个93，秩次为1和2。同样，在向量B，中，80的秩次为1,39的秩次为6

\[\rho=1-\frac{6\sum\limits_{k=1}^m{d_k^2}}{n(n^2-1)}=1-\frac{6\times 48}{6(6^2-1)}=-0.37143 \]

斯皮尔曼秩相关系数函数代码

## 函数
    webTJ.Datamining.getSPKDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oSPKDis=webTJ.Datamining.getSPKDis(oArr1,oArr2); 
webTJ.display("斯皮尔曼秩相关系数 = "+oSPKDis,0);

斯皮尔曼秩相关系数矩阵函数代码

## 函数
    webTJ.Datamining.getSPKDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oSPKDiss=webTJ.Datamining.getSPKDiss(oArrs); 
webTJ.show(oSPKDiss,2);

斯皮尔曼秩相关系数推论和证明

设有序列数据25、38、42、36。

将数据分别正序和倒序排序，则有25、36、38、42和42、38、36、25。两组排序后数据的秩为4、3、2、1和1、2、3、4，秩差平方和为\((4-1)^2+(3-2)^2+(2-3)^2+(1-4)^2=20\)。

将该样本按正序分为两个相同组，25、36、38、42和25、36、38、42，秩为4、3、2、1和4、3、2、1，秩差平方和为0。

如果将数据分为两组，第一组为正序、第二组为原序列或乱序，即42、38、36、25和原序列25、38、42、36，或42、38、36、25和乱序列36、42、38、25，不同对比组秩为4、3、2、1和4、2、1、3，或4、3、2、1和3、1、2、4，秩差平方和为

一般情况下，设有n个样本的序列数据，将数据分别正序和倒序排序后，秩差平方和S为\((4-4)^2+(3-2)^2+(2-1)^2+(1-3)^2=6\)和\((4-3)^2+(3-1)^2+(2-2)^2+(1-4)^2=14\)。

推论一：将数据序列分别正序和倒序排序后，正序序列和倒序序列数据的秩差平方和大于任何不同排序间的秩差平方和。

\[S=(n-1)^2+(n-3)^2+(n-7)]^2+\dots=(n^2+1^2-2\times 1\times n)+(n^2+3^2-2\times 3\times n)+(n^2+5^2-2\times 5\times n)+\dots=n\times n^2+[1^2+3^2+5^2+\dots+(2n-1)^2]-2\times n\times [1+3+5+\dots+(2n-1)]=n^3+\frac{1}{3}n(4n^2-1)-2n\times n^2=\frac{1}{3}n(n^2-1) \]

推论二：两个具有n个元素的不同数据序列，秩差平方和最小值为0、最大值为\(S=\frac{1}{3}n(n^2-1)\)。

斯皮尔曼秩相关系数：

\[\rho=1-\frac{6\sum\limits_{k=1}^m{d_k^2}}{n(n^2-1)}=1-\frac{6\times S}{n(n^2-1)} \]

秩差平方和取最小值0，斯皮尔曼秩相关系数为1；秩差平方和取最大值\(S=\frac{1}{3}n(n^2-1)\)，斯皮尔曼秩相关系数为-1。

（证毕）

3、肯德尔秩相关系数（Kendall Rank Correlation）

肯德尔秩相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间，当肯德尔相关系数为1时，表示两个随机变量拥有一致的等级相关性；当肯德尔相关系数为-1时，表示两个随机变量拥有完全相反的等级相关性；当肯德尔相关系数为0时，表示两个随机变量是相互独立的。

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的肯德尔秩相关系数公式：

\[\tau=\frac{2P}{\frac{1}{2}n(n-1)}-1=\frac{4P}{n(n-1)}-1 \]

式中\(P\)为\(X_{i}\)对\(X_{j}\)或\(X_{j}\)对\(X_{i}\)的秩次贡献之和。对\(P\)值的理解参见下例：

设有8名学生身高和体重统计数据如下表，

学生ABCDEFGH
身高(cm)175178165180173176170168
体重(kg)7772687570806564

计算肯德尔秩相关系数。

解、通常情况下，人的身高和体重呈正比例关系，先将升高样本按大到小排序，

学生ABCDEFGH
身高(cm)180178176175173170168165
体重(kg)7572807770656468

对身高排序后可以看出身高最高者体重不是最重者，但是身材高者体重总体来说还是较重的，为进一步体现两者关系，计算两者的秩次和体重的秩次贡献，数据如下表：

学生ABCDEFGH
身高(cm)12345678
体重(kg)34125786
贡献($P_i$)54543100

表中A学生身材最高（秩次为1），体重排名为3（秩次为1），在A学生后面所有其他学生体重中，A学生体重超过5个人，取贡献\(P_1=5\)。A学生身材最高，他的体重完全贡献分应该能达到7分。

B学生身材第二高（秩次为2），体重排名为4（秩次为4），在B学生后面所有其他学生体重中，B学生体重超过4个人，取贡献\(P_2=4\)。其他学生体重贡献得分同理。

体重贡献和：\(P=5+4+5+4+3+1+0+0=22\)。肯德尔秩相关系数为，

\[\tau=\frac{2P}{\frac{1}{2}n(n-1)}-1=\frac{4P}{n(n-1)}-1=\frac{4\times 22}{8(8-1)}-1\approx 0.5714 \]

如果先对体重继续排序，结果如下：

学生ABCDEFGH
身高(cm)176175180178173165170168
体重(kg)8077757270686564

秩次和身高的秩次贡献，数据如下表：

学生ABCDEFGH
身高(cm)34125867
体重(kg)12345678
贡献($P_i$)54543010

体重贡献和：\(P=5+4+5+4+3+1+0+0=22\)。肯德尔秩相关系数仍为\(0.5714\)。

肯德尔秩相关系数函数代码

## 函数
    webTJ.Datamining.getKNDDis(arrs,i,j);
##参数
    【arrs,i,j】
    【二维数组,第i个向量,第j个向量】

代码样例

webTJ.clear();
var oArr1=[175,178,165,180,173,176,170,168];
var oArr2=[77,72,68,75,70,80,65,64];
var oKNDDis=webTJ.Datamining.getKNDDis(oArr1,oArr2); 
webTJ.display("肯德尔秩相关系数 = "+oKNDDis,0);        
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
oKNDDis=webTJ.Datamining.getKNDDis(oArr1,oArr2); 
webTJ.display("肯德尔秩相关系数 = "+oKNDDis,0);

肯德尔秩相关系数矩阵函数代码

## 函数
    webTJ.Datamining.getKNDDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oKNDDiss=webTJ.Datamining.getKNDDiss(oArrs); 
webTJ.show(oKNDDiss,2);

4、余弦相似度(Cosine Similarity)

几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中用这一概念来衡量样本向量之间的差异。夹角余弦的取值范围为[-1,1]。夹角余弦越大表
示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1。欧氏距离是最常见的距离度量，而余弦相似度则是最常见的相似度度量，很多的距离度量和相似度度量都是基于这两者的变形和衍生。

设有m个n维向量\((X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m\)，向量\((X_{i1},X_{i2},\dots,X_{in})\)与\((X_{j1},X_{j2},\dots,X_{jn})\)间的余弦相似度：

\[\cos(\theta)=\frac{\sum\limits_{k=1}^nX_{ik}\times X_{jk}}{\sqrt{\sum\limits_{k=1}^nX_{ik}^2\times\sum\limits_{k=1}^nX_{jk}^2}} \]

根据附表I中学生成绩表计算第3名和第5名学生成绩之间的余弦相似度。

解：第3名成绩向量为\(A(76,93,93,79,71,27)\)、第5名成绩向量为\(B(80,39,48,75,41,52)\)，两者余弦相似度为，

\(\sum\limits_{k=1}^6X_{ik}\times X_{jk}=76\times 80+93\times 39+93\times 48+79\times 75+71\times 41+27\times 52=24411\)
\(\sum\limits_{k=1}^6X_{ik}^2=76^2+93^2+93^2+79^2+71^2+27^2=35085\)
\(\sum\limits_{k=1}^6X_{jk}^2=80^2+39^2+48^2+75^2+41^2+52^2=20235\)

\[\cos(\theta)=\frac{\sum\limits_{k=1}^6X_{ik}\times X_{jk}}{\sqrt{\sum\limits_{k=1}^6X_{ik}^2\times\sum\limits_{k=1}^6X_{jk}^2}}=\frac{24411}{\sqrt{35085\times 20235}}=0.916164 \]

夹角余弦与向量的长度无关，如向量(1,2)和(2,4)的夹角余弦与向量(1,2)和(10,20)的相等。即，

\[\frac{1\times 2+2\times 4}{\sqrt{(1^2+2^2)\times (2^2+4^2)}}=\frac{1\times 20+2\times 40}{\sqrt{(1^2+2^2)\times (10^2+20^2)}}=1 \]

借助三维坐标系来看下欧氏距离和余弦相似度的区别：

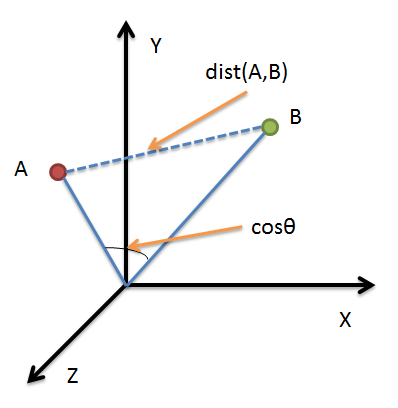
从图上可以看出距离度量衡量的是空间各点间的绝对距离，跟各个点所在的位置坐标（即个体特征维度的数值）直接相关；而余弦相似度衡量的是空间向量的夹角，更加的是体现在方向上的差异，而不是位置。如果保持A点的位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦相似度cosθ是保持不变的，因为夹角不变，而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征，分别适用于不同的数据分析模型：欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异；而余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦相似度对绝对数值不敏感）。

余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感。因此没法衡量每个维数值的差异，会导致这样一个情况：比如用户对内容评分，5分制，X
和Y两个用户对两个内容的评分分别为(1,2)和(4,5)，使用余弦相似度得出的结果是0.98，两者极为相似，但从评分上看X似乎不喜欢这2个内容，而Y比较喜欢。余弦相似度对数值的不敏感导致了结果的误差，有时需要修正这种不合理性。

调整余弦相似度，将所有维度上的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为(-2,-1)和(1,2)，再用余弦相似度计算，得到-0.8，相似度为负值并且差异不小，但显然更加符合现实。

余弦相似度函数代码

## 函数
    webTJ.Datamining.getCOSDis(arr1,arr2);
##参数
    【arr1,arr2】
    【一维数组1,一维数组2】

代码样例

webTJ.clear();
var oArr1=[76,93,93,79,71,27];
var oArr2=[80,39,48,75,41,52];
var oCOSDis=webTJ.Datamining.getCOSDis(oArr1,oArr2); 
webTJ.display("余弦相似度 = "+oCOSDis,0);

余弦相似度矩阵函数代码

## 函数
    webTJ.Datamining.getCOSDiss(arrs);
##参数
    【arrs】
    【二维数组】

代码样例

webTJ.clear();
var oStr="67,63,73,75,44,91|74,69,66,94,81,55|76,93,93,79,71,27|65,38,85,85,61,45|80,39,48,75,41,52|72,80,70,88,86,43|60,50,91,95,42,64|77,49,69,50,89,55|65,89,50,70,99,85|78,41,55,89,71,28";
var oArrs=webTJ.getArrs(oStr,"|",",");
oArrs=webTJ.Array.getQuantify(oArrs);
var oCOSDiss=webTJ.Datamining.getCOSDiss(oArrs); 
webTJ.show(oCOSDiss,2);


代码窗口

注：可将例题实例代码复制、粘贴到“代码窗口”，点击“运行代码”获得计算结果（Ctrl+C:复制；Ctrl+V:粘贴；Ctrl+A:全选）

运行效果

posted @ 2017-04-03 17:31  银河统计  阅读(3580)  评论(0)  编辑  收藏  举报