统计基本指标 - 网络统计学类函数(4)
 (2017-03-21 银河统计)
(2017-03-21 银河统计)本文着重解决统计函数计算问题。在数组类函数(webTJ.Array)和矩阵类函数(webTJ.Matrix)基础上,可以比较容易设计统计公式类函数(webTJ.Formula)和统计方法类函数(webTJ.Method)。本文按一元和二元统计样本分类介绍统计公式类函数及样例代码。
本网页中所有统计函数和代码样例都可以复制、粘贴到网页尾部“代码窗口”运行通过。为方便运行本文中样例代码,可打开网络统计学代码调试窗口,复制、粘贴代码到数据处理代码窗口中运行即可。
统计基本指标(子类名称:webTJ.Formula)一览表
| 序号 | 函数名称 | 参数1 | 参数2 | 参数3 | 功能 | 备注 |
|---|---|---|---|---|---|---|
| 1 | getCount(arr) | 一维数组 | * | * | 样本容量(计数) | * |
| 2 | getSum(arr) | 一维数组 | * | * | 样本求和 | * |
| 3 | getMean(arr) | 一维数组 | * | * | 算数平均数 | * |
| 4 | getWMean(arrs) | 二维数组 | * | * | 加权算术平均数 | * |
| 5 | getHMean(arr) | 一维数组 | * | * | 调和平均数 | * |
| 6 | getWHMean(arrs) | 二维数组 | * | * | 加权调和平均数 | * |
| 7 | getGMean(arr) | 一维数组 | * | * | 几何平均数 | * |
| 8 | getWGMean(arrs) | 二维数组 | * | * | 加权几何平均数 | * |
| 9 | getMedian(arr) | 一维数组 | * | * | 单项式样本中位数 | * |
| 10 | getSMedian(arrs) | 二维数组 | * | * | 单项式分组样本中位数 | * |
| 11 | getGMedian(arrs) | 二维数组 | * | * | 组距式分组样本中位数 | * |
| 12 | getQuantile(arr,p) | 一维数组 | 分位百分比 | * | 未分组样本分位数 | * |
| 13 | getGQuantile(arrs,p) | 二维数组 | 分位百分比 | * | 分组(组距式)样本分位数 | * |
| 14 | getMode(arr) | 一维数组 | * | * | 单项式样本众数 | * |
| 15 | getGMode(arrs) | 二维数组 | * | * | 组距式样本众数 | * |
| 16 | getRange(arr) | 一维数组 | * | * | 全距 | * |
| 17 | getMD(arr) | 一维数组 | * | * | 平均差 | * |
| 18 | getIQR(arr) | 一维数组 | * | * | 四分位差 | * |
| 19 | getVariance(arr,k) | 一维数组 | k有偏或无偏估计 | * | 方差和样本方差 | 方差(k=0);样本方差(k=1) |
| 20 | getSD(arr,k) | 一维数组 | k有偏或无偏估计 | * | 标准差和样本标准差 | 标准差(k=0);样本标准差(k=1) |
| 21 | getVR(arr) | 一维数组 | * | * | 极差(全距)系数 | * |
| 22 | getVMD(arr) | 一维数组 | * | * | 平均差系数 | * |
| 23 | getVSD(arr) | 一维数组 | * | * | 标准差系数 | * |
| 24 | getPKewness(arr) | 一维数组 | * | * | 皮尔逊偏态系数 | * |
| 25 | getMOM(arr,k) | 一维数组 | k阶矩 | * | 原点矩 | * |
| 26 | getMCM(arr,k) | 一维数组 | k阶矩 | * | 中心矩 | * |
| 27 | getSkewness(arr,k) | 一维数组 | k有偏或无偏估计 | * | 动差偏态系数 | * |
| 28 | getKurtosis(arr,k) | 一维数组 | k有偏或无偏估计 | * | 峰度 | * |
注:本网页中所有数据管理类函数和代码样例都可以复制、粘贴到网页尾部“代码窗口”运行通过
一、平均指标统计函数###
平均指标又称集中趋势指标,它是样本平均水平的代表,也是数据集中趋势的测度。平均指标用以反映社会经济现象总体各单位某一数量标志在一定时间、地点条件下所达到的一般水平的综合指标。根据样本数据类型,集中趋势测度大致可以分为数值测试法和位置测定法两类。
数值测试法主要包括算数平均数、调和平均数和几何平均数,位置测定法包括中位数、指数和分位数等。
1、样本容量(Sample Size) [返回]
样本容量又称“样本数”、“样本大小”。在一个样本中所包含的个案或单元数。一般来说,样本容量主要由精确度、同质性、财力、抽样类型、分析类别等因素决定。在抽样调查中,样本容量的确定很重要。因为样本容量太大,会造成人力、物力和财力的很大浪费;样本容量太小,会使抽样误差太大,使调查结果与实际情况相差很大,影响调查的效果。
从计算角度看,当样本总体较大时,确定样本容量为计数问题。
案例一:设有某学校学生英语成绩如下:
95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88
共有多少名学生的成绩?
函数代码
## 函数
webTJ.Formula.getCount(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
var oLen=webTJ.Formula.getCount(oArr);
webTJ.display("样本容量 = "+oLen,0);
2、样本求和(Summation) [返回]
设有样本,样本合计统计量为,
函数代码
## 函数
webTJ.Formula.getSum(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oArr = [3,5,8,10,8,7,10,3,5,3];
var oSum=webTJ.Formula.getSum(oArr);
webTJ.display("样本合计 = "+oSum,0);
3、算数平均数(Arithmetic Mean) [返回]
算术平均数(arithmetic mean),又称均值,是统计学中最基本、最常用的一种平均指标。算术平均数是将各单位的标志值直接相加得出标志总量,再除以总体单位数,就得到简单算术平均数。通过算术平均数,可以用来求出一定观察期内预测目标的时间数列的算术平均数作为下期预测值的一种最简单的时序预测法。用公式表示为:
函数代码
## 函数
webTJ.Formula.getMean(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oArr = [3,5,8,10,8,7,10,3,5,3];
var oMean=webTJ.Formula.getMean(oArr);
webTJ.display("简单算术平均数 = "+oMean,0);
4、加权算术平均数(Weighted Arithmetic Mean) [返回]
加权平均数即将各样本乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。
当样本被分组或单项式样本重复项较多时,可根据样本分组频数(频率)或样本项发生次数(比重),将各样本乘以相应的权数,然后加总求和得到加权平均数。这里的频数(频率)或发生次数(比重)称为权数。权数一般有两种表现形式,一是绝对数(频数)表示,另一个是用相对数(频率)表示,相对数是用绝对数计算出来的百分数(%)表示的,又称比重。
设有样本,为第个样本的权数,则有加权算术平均数公式,
案例二:根据本文前面某学校100名学生英语成绩样本,可以整理为单项式分组表如下,
| 序号 | 数据项 | 权数 | 序号 | 数据项 | 权数 | 序号 | 数据项 | 权数 |
|---|---|---|---|---|---|---|---|---|
| 1 | 95 | 4 | 21 | 87 | 1 | 41 | 48 | 1 |
| 2 | 74 | 1 | 22 | 88 | 4 | 42 | 93 | 3 |
| 3 | 31 | 3 | 23 | 86 | 3 | 43 | 39 | 1 |
| 4 | 68 | 3 | 24 | 47 | 3 | 44 | 44 | 1 |
| 5 | 50 | 2 | 25 | 51 | 2 | 45 | 96 | 1 |
| 6 | 59 | 2 | 26 | 82 | 3 | 46 | 34 | 2 |
| 7 | 33 | 3 | 27 | 90 | 2 | 47 | 56 | 2 |
| 8 | 41 | 4 | 28 | 43 | 2 | 48 | 60 | 2 |
| 9 | 81 | 1 | 29 | 73 | 2 | 49 | 98 | 1 |
| 10 | 53 | 3 | 30 | 97 | 1 | 50 | 78 | 1 |
| 11 | 91 | 2 | 31 | 83 | 1 | 51 | 40 | 1 |
| 12 | 35 | 1 | 32 | 85 | 2 | 52 | 49 | 1 |
| 13 | 57 | 3 | 33 | 38 | 1 | 53 | 94 | 1 |
| 14 | 58 | 1 | 34 | 70 | 3 | |||
| 15 | 63 | 4 | 35 | 61 | 2 | |||
| 16 | 77 | 1 | 36 | 71 | 1 | |||
| 17 | 62 | 2 | 37 | 42 | 1 | |||
| 18 | 92 | 2 | 38 | 99 | 1 | |||
| 19 | 37 | 2 | 39 | 55 | 1 | |||
| 20 | 36 | 1 | 40 | 65 | 1 |
单项式分组样本加权平均数为,
将100名学生英语成绩样本整理为组距式分组表如下,
| 下限 | 上限 | 组中值 | 权数 |
|---|---|---|---|
| 30 | 40 | 35 | 14 |
| 40 | 50 | 45 | 14 |
| 50 | 60 | 55 | 16 |
| 60 | 70 | 65 | 14 |
| 70 | 80 | 75 | 9 |
| 80 | 90 | 85 | 15 |
| 90 | 100 | 95 | 18 |
| 合计 | 100 |
组距式分组样本加权平均数为,
函数代码
## 函数
webTJ.Formula.getWMean(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
//简单算术平均数
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88"; //100名学生成绩字符串
var oArr=webTJ.getArr(oStr,","); //成绩字符串转换为一维数组
var oArr=webTJ.Array.getQuantify(oArr); //量化数组
var oMean=webTJ.Formula.getMean(oArr); //计算算术平均数
webTJ.display("简单算术平均数 = "+oMean,0);
//单项式加权算术平均数
oStr="95,4|74,1|31,3|68,3|50,2|59,2|33,3|41,4|81,1|53,3|91,2|35,1|57,3|58,1|63,4|77,1|62,2|92,2|37,2|36,1|87,1|88,4|86,3|47,3|51,2|82,3|90,2|43,2|73,2|97,1|83,1|85,2|38,1|70,3|61,2|71,1|42,1|99,1|55,1|65,1|48,1|93,3|39,1|44,1|96,1|34,2|56,2|60,2|98,1|78,1|40,1|49,1|94,1"; //学生成绩单项式分组字符串
var oArrs=webTJ.getArrs(oStr,"|",","); //成绩单项式分组字符串转换为二维数组
oArrs=webTJ.Array.getQuantify(oArrs); //量化数组
var oWMean1=webTJ.Formula.getWMean(oArrs); //计算单项式加权算术平均数
webTJ.display("单项式加权算术平均数 = "+oWMean1,0);
//组距式加权算术平均数
var oWrrs=[[35,14],[45,14],[55,16],[65,14],[75,9],[85,15],[95,18]]; //学生成绩组距式数组
var oWMean2=webTJ.Formula.getWMean(oWrrs); //计算组距式加权算术平均数
webTJ.display("组距式加权算术平均数 = "+oWMean2,0);
注:组距式加权算术平均数为65.7,简单算术平均数和单项式加权算术平均数为64.8,为什么?“组距式加权算术平均数是真正平均数的估计值”这话对吗?
5、调和平均数(Harmonic Mean) [返回]
调和平均数(harmonic mean)又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数。调和平均数是平均数的一种。调和平均数是算术平均数的变形,它的计算公式如下:
函数代码
## 函数
webTJ.Formula.getHMean(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oArr = [3,5,8,10,8,7,10,3,5,3];
var oHMean=webTJ.Formula.getHMean(oArr);
webTJ.display("调和平均数 = "+oHMean,0);
6、加权调和平均数(Weighted Harmonic Mean) [返回]
当样本被分组或单项式样本重复项较多时,可根据样本分组频数(频率)或样本项发生次数(比重)计算加权调和平均数。设有样本,为第个样本的权数,则有加权调和平均数公式,
案例三:某农贸市场三种蔬菜价格及销售额信息如下表,
| 品种 | 价格(元)- | 销售额(元)- | 销售量(千克) |
|---|---|---|---|
| 甲 | 1.5 | 3750 | 2500 |
| 乙 | 1.2 | 5400 | 4500 |
| 丙 | 2.5 | 4500 | 1800 |
| 合计 | 13650 | 8800 |
计算三种产品的平均价格。
解:计算任何统计指标应首先明确指标基本含义。,当获得的商品销售信息只有商品价格和销售额时,首先应该计算出每种商品的销售量(),然后合计销售额和销售量,最后计算出平均价格。将整个计算过程合并,即为加权调和平均数。计算公式如下:
三种商品平均价格为1.55(元/千克)。式中,分子计算商品总销售额,分母计算商品总销售量。
函数代码
## 函数
webTJ.Formula.getWHMean(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
var oArrs = [[3750,1.5],[5400,1.2],[4500,2.5]];
var oWHMean=webTJ.Formula.getWHMean(oArrs);
webTJ.display("加权调和平均数 = "+oWHMean,0);
7、几何平均数(Geometric Mean) [返回]
几何平均数(geometric mean)是指n个观察值连乘积的n次方根。几何平均数多用于计算平均比率和平均速度。如:平均利率、平均发展速度、平均合格率等。它的计算公式如下:
案例四:某产品原件出厂需要3道工序,1000个原件经过各工序后,成品数分别为950、910、和860个,求该产品总合格率和各工序平均合格率合格率。
解、该产品总合格率为,
产品总合格率也可以表示为连乘形式,即,
也就是说,经过m道工序,各工序合格率的乘积为总合格率。记各工序合格率为,总合格率为,则有,
令各工序平均合格率为,计算公式变为,
解得,
所以,计算不同时期或阶段比率数据平均比率时,应该用几何平均算法,而不是简单算术平均数。
在本案例中,
即各工序平均合格率为95.097%。
函数代码
## 函数
webTJ.Formula.getGMean(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oArr = [0.95,0.9579,0.945055];
var oGMean=webTJ.Formula.getGMean(oArr);
webTJ.display("几何平均数 = "+oGMean,0);
8、加权几何平均数(Weighted Geometric Mean) [返回]
分组或单项式样本重复项较多时,可根据样本分组频数(频率)或样本项发生次数(比重)计算加权几何平均数。设有样本,为第个样本的权数,则有加权调和平均数公式,
案例五:在某银行存款15年,按复利计算利息,利率和实施年度表如下:
| 年利率(%) | 年数 |
|---|---|
| 5 | 2 |
| 3 | 4 |
| 4 | 6 |
| 3.5 | 3 |
计算各年平均利率。
即各年平均利率为3.765%。
函数代码
## 函数
webTJ.Formula.getWGMean(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
var oArrs = [[1.05,2],[1.03,4],[1.04,6],[1.035,3]];
var oWGMean=webTJ.Formula.getWGMean(oArrs);
webTJ.display("加权几何平均数 = "+oWGMean,0);
平均数的基本性质:
I、各样本值与样本平均数离差之和为零
II、各样本值与样本平均数离差平方和最小,即,
证明:设有一实数m,令,
极值存在的必要条件是一阶导数为零,即,
解得,
又因为,
二阶导数为正,有极小值。所以当时,(证毕)
III、平均数()、调和平均数()和几何平均数()的关系
证明:
仅以两个样本情况来证明如下,
令,
则,
即,
再令,
则,
即,
所以,
(证毕)
9、中位数(Median)
中位数是指将数据按大小顺序后,居于数列中间位置的那个数据。从中位数的定义可知,样本数据中有一半小于中位数,一半大于中位数。在数列中出现了极端样本值的情况下,用中位数作为代表值要比用算术平均数更好,因为中位数不受极端变量值的影响。当次数分布偏态时,中位数的代表性会受到影响。
I、单项式样本中位数 [返回]
设有未分组样本,将样本按大小排序。设排序的结果为,
则单项式样本中位数公式为,
现有样本,
95,74,31,68,50,68,59,33,41
计算中位数。
首先排序样本,
31,33,41,50,59,68,68,74,95
由于样本量为奇数,样本中间项数据为59,即中位数为59。
如果排序后样本容量为偶数,
31,33,41,50,59,67,68,74,80,95
这时样本有两个中间项数据59,67,中位数为,
函数代码
## 函数
webTJ.Formula.getMedian(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oArr1 = [31,33,41,50,59,68,68,74,95];
var oArr2 = [31,33,41,50,59,67,68,74,80,95];
var oMedian1=webTJ.Formula.getMedian(oArr1);
var oMedian2=webTJ.Formula.getMedian(oArr2);
webTJ.display("中位数1 = "+oMedian1,0);
webTJ.display("中位数2 = "+oMedian2,0);
II、单项式分组样本中位数 [返回]
在分组单项式样本情况下,样本单项,样本单项单项分组次数。先计算各组的累计次数,然后根据中位点确定中位数所在组,中位数所在组样本标准值就是中位数。
某工厂工人产量数据表如下:
| 日产量分组(件) | 工人数(个) | 累计次数(向下) |
|---|---|---|
| 4 | 8 | 8 |
| 5 | 22 | 30 |
| 6 | 42 | 72 |
| 7 | 38 | 110 |
| 8 | 17 | 127 |
| 9 | 3 | 130 |
| 合计 | 130 | * |
计算中位数。
解、中位点所在位置,,根据累计次数,属于72所对应的数据项6,即中位数为6件。
函数代码
## 函数
webTJ.Formula.getSMedian(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
var oArrs = [[4,8],[5,22],[6,42],[7,38],[8,17],[9,3]];
var oSMedian=webTJ.Formula.getSMedian(oArrs);
webTJ.display("单项式分组中位数 = "+oSMedian,0);
III、组距式分组样本中位数 [返回]
对于按组距分组的样本,中位数计算比较繁琐,计算步骤如下:
a.计算分组频数向上和向下累计;
b.根据分组频数累计总和确定中位点;
c.由中位点和累计数列确定中位数所在组(当某向下累计数大于中位点时,该累计数对应的分组为中位数所在组);
d.利用中位数所在组次数、组距()、上限和下限()、以及中位数所在组和上下相邻组次累计数(),中位数估计公式为,
下限公式:
上限公式:
案例六:根据下面例表的数据,计算50名工人日加工零件数的中位数。
| 按零件数分组(个) | 频数(人) | 向下累计 | 向上累计 |
|---|---|---|---|
| 105-110 | 3 | 3 | 50 |
| 110-115 | 5 | 8 | 47 |
| 115-120 | 8 | 16 | 42 |
| 120-125 | 14 | 30 | 34 |
| 125-130 | 10 | 40 | 20 |
| 130-135 | 6 | 46 | 10 |
| 135-140 | 4 | 50 | 4 |
解、首先计算向下累计向上累计数。根据表中数据,
中位点,
由于在向下累计列中,,中位数所在组为30对应的分组120-125。则有,
下限公式:
上限公式:
函数代码
## 函数
webTJ.Formula.getGMedian(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
var oArrs = [[105,110,3],[110,115,5],[115,120,8],[120,125,14],[125,130,10],[130,135,6],[135,140,4]];
var oGMedian=webTJ.Formula.getGMedian(oArrs);
webTJ.display("组距式分组中位数 = "+oGMedian,0);
10、样本分位数(Quantile)
样本p分位数(sample quantile of order p )是一种样本特征量。设给定一个概率值 ,该总体的分布函数为,则方程的解即称为该分布的分位数。中位数就是50%的分位数,常用的还有25%下四分位数和75%上四分位数。当分布函数为连续型变量时,可以通过解方程求得任意点的分位数,但在用样本值(离散数据)计算分位数时,经验分布是跳跃的,无法用解方程的方法计算分位数。这可采用插值方法处理。
分位数根据其将数列等分的形式不同可以分为中位数,四分位数,十分位数、百分位数等等。人们经常会将数据划分为4个部分,每一个部分大约包含有1/4即25%的数据项。这种划分的临界点即为四分位数。四分位数作为分位数的一种形式,在统计中有着十分重要的意义和作用。
I、未分组样本分位数 [返回]
设有未分组样本,将样本按大小排序。设排序的结果为,
记为不超过的最大整数,,此时分位数在与之间。
记表示的小数部分,则样本的分位数为,
案例七:设有某城市15例火灾损失金额(万元)数据如下:
5.98,3.81,1.98,0.44,0.39,1.81,3.79,0.9,3.9,4.13,4.72,7.16,0.71,19.13,9.72
计算中位数、上下四分位数、40%和80%分位数。
解、样本排序,
0.39,0.44,0.71,0.9,1.81,1.98,3.79,3.81,3.9,4.13,4.72,5.98,7.16,9.72,19.13
中位数:
,
,
,
。
下四分位数:
,
,
,
。
上四分位数:
,
,
,
。
40%分位数:
,
,
,
。
80%分位数:
,
,
,
。
函数代码
## 函数
webTJ.Formula.getQuantile(arr,p);
##参数
【arr,p】
【一维数组,分位百分比】
代码样例
webTJ.clear();
var oStr="0.39,0.44,0.71,0.9,1.81,1.98,3.79,3.81,3.9,4.13,4.72,5.98,7.16,9.72,19.13";
var oArr=webTJ.getArr(oStr,",");
var oQuantile=webTJ.Formula.getQuantile(oArr,0.5);
webTJ.display("中位数 = "+oQuantile,0);
oQuantile=webTJ.Formula.getQuantile(oArr,0.25);
webTJ.display("下四分位数 = "+oQuantile,0);
oQuantile=webTJ.Formula.getQuantile(oArr,0.75);
webTJ.display("上四分位数 = "+oQuantile,0);
oQuantile=webTJ.Formula.getQuantile(oArr,0.4);
webTJ.display("40%中位数 = "+oQuantile,0);
oQuantile=webTJ.Formula.getQuantile(oArr,0.8);
webTJ.display("80%中位数 = "+oQuantile,0);
II、分组(组距式)样本分位数 [返回]
对于按组距分组的样本,分位数计算步骤如下:
a.计算分组频数向上和向下累计;
b.根据分组频数累计总和确定分位点;
c.由分位点和累计数列确定分位数所在组(当某向下累计数大于分位点时,该累计数对应的分组为分位数所在组);
d.利用分位数所在组次数、组距()、上限和下限()、以及分位数所在组和上下相邻组次累计数()。
分位数估计公式为,
下限公式:
上限公式:
案例八:某企业职工按月工资的分组资料如下:
| 按月工资分组(元) | 职工人数(人) | 向上累计职工人数 | 向下累计职工人数 |
|---|---|---|---|
| 600以下 | 23 | 23 | 566 |
| 600—700 | 120 | 143 | 543 |
| 700—800 | 150 | 293 | 423 |
| 800—900 | 135 | 428 | 273 |
| 900—1000 | 95 | 523 | 138 |
| 1000以上 | 43 | 566 | 43 |
| 合计 | 566 | * | * |
计算中位数、上下四分位数、40%和60%分位数。
解、
中位数:
下四分位数:
上四分位数:
40%分位数:
80%分位数:
函数代码
## 函数
webTJ.Formula.getGQuantile(arrs,p);
##参数
【arrs,p】
【二维数组】
代码样例
webTJ.clear();
var oArrs=[[0,600,23],[600,700,120],[700,800,150],[800,900,135],[900,1000,95],[1000,9999,43]];
var oGQuantile=webTJ.Formula.getGQuantile(oArrs,0.5);
webTJ.display("中位数 = "+oGQuantile,0);
oGQuantile=webTJ.Formula.getGQuantile(oArrs,0.25);
webTJ.display("下四分位数 = "+oGQuantile,0);
oGQuantile=webTJ.Formula.getGQuantile(oArrs,0.75);
webTJ.display("上四分位数 = "+oGQuantile,0);
oGQuantile=webTJ.Formula.getGQuantile(oArrs,0.4);
webTJ.display("40%分位数 = "+oGQuantile,0);
oGQuantile=webTJ.Formula.getGQuantile(oArrs,0.8);
webTJ.display("80%分位数 = "+oGQuantile,0);
11、众数(Mode)
众数是指一组数据中出现次数最多的那个数据,一组数据可以有多个众数,也可以没有众数。所谓众数是指社会经济现象中最普遍出现的标志值。从分布角度看,众数是具有明显集中趋势的数值。
统计上把在一组数据中出现次数最多的变量值叫做众数。用表示。它主要用于定类(品质标志)数据的集中趋势,当然也适用于作为定序(品质标志)数据以及定距和定比(数量标志)数据集中趋势的测度值。
I、单项式样本众数 [返回]
由品质数列和单项式变量数列确定众数比较容易,哪个样本值出现的次数最多,它就是众数。例如,
某制鞋厂要了解消费者最需要哪种型号的男皮鞋,调查了某百货商场某季度男皮鞋的销售情况,得到资料如下表(某商场某季度男皮鞋销售情况):
| 男皮鞋号码(厘米) | 销售量(双) |
|---|---|
| 24 | 12 |
| 24.5 | 84 |
| 25 | 118 |
| 25.5 | 541 |
| 26 | 320 |
| 26.5 | 104 |
| 27 | 52 |
| 合计 | 1200 |
从表中可以看到,25.5厘米的鞋号销售量最多,众数为25.5厘米。
单项式样本众数计算的步骤为,
a.提取样本唯一项并排序;
b.根据唯一项统计各项频数;
c.由频数确定众数。
案例九:现有200名学生统计学成绩如下:
57,45,74,96,71,65,54,60,88,92,45,41,61,59,72,44,67,68,77,48,85,70,70,55,96,47,44,99,93,49,62,77,62,65,68,64,69,64,52,43,99,60,74,70,70,75,79,78,67,75,88,70,62,76,77,63,73,70,41,54,98,78,74,66,70,76,63,76,66,99,63,61,65,70,73,74,60,71,61,42,93,72,69,61,69,60,78,74,73,84,60,63,65,68,77,64,79,75,43,99,52,73,73,71,63,72,75,69,48,80,87,63,73,61,71,66,77,60,75,51,63,79,71,74,66,73,70,63,98,47,82,52,51,43,41,71,61,46,67,99,65,92,80,55,44,54,63,94,88,70,76,45,71,46,84,52,91,98,97,94,59,74,72,84,54,46,45,87,44,88,46,61,92,53,41,65,66,91,46,97,96,42,96,79,80,54,60,47,67,59,49,92,80,41,92,50,59,74,93,72
计算众数。
解、
提取样本唯一项并排序,
41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,57,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,82,84,85,87,88,91,92,93,94,96,97,98,99
根据唯一项统计各项频数,
| 序号 | 唯一项 | 频数 | 序号 | 唯一项 | 频数 | 序号 | 唯一项 | 频数 |
|---|---|---|---|---|---|---|---|---|
| 1 | 41 | 5 | 18 | 60 | 7 | 35 | 77 | 5 |
| 2 | 42 | 2 | 19 | 61 | 7 | 36 | 78 | 3 |
| 3 | 43 | 3 | 20 | 62 | 3 | 37 | 79 | 4 |
| 4 | 44 | 3 | 21 | 63 | 9 | 38 | 80 | 4 |
| 5 | 45 | 4 | 22 | 64 | 3 | 39 | 82 | 1 |
| 6 | 46 | 5 | 23 | 65 | 6 | 40 | 84 | 3 |
| 7 | 47 | 3 | 24 | 66 | 5 | 41 | 85 | 1 |
| 8 | 48 | 2 | 25 | 67 | 4 | 42 | 87 | 2 |
| 9 | 49 | 2 | 26 | 68 | 3 | 43 | 88 | 4 |
| 10 | 50 | 1 | 27 | 69 | 4 | 44 | 91 | 2 |
| 11 | 51 | 2 | 28 | 70 | 14 | 45 | 92 | 5 |
| 12 | 52 | 4 | 29 | 71 | 7 | 46 | 93 | 3 |
| 13 | 53 | 1 | 30 | 72 | 5 | 47 | 94 | 2 |
| 14 | 54 | 5 | 31 | 73 | 7 | 48 | 96 | 4 |
| 15 | 55 | 2 | 32 | 74 | 8 | 49 | 97 | 2 |
| 16 | 57 | 1 | 33 | 75 | 5 | 50 | 98 | 2 |
| 17 | 59 | 4 | 34 | 76 | 4 | 51 | 99 | 3 |
根据频数表可知,学生成绩为70的最多、有14人,故统计学学生成绩众数为70。
函数代码
## 函数
webTJ.Formula.getMode(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="57,45,74,96,71,65,54,60,88,92,45,41,61,59,72,70,67,68,77,48,85,70,70,55,96,47,44,99,93,49,62,77,62,65,68,64,69,64,52,43,99,60,74,70,70,75,79,78,67,75,88,70,62,76,77,63,73,70,41,54,70,78,74,66,70,76,63,76,66,70,63,61,65,70,73,74,60,71,61,42,93,72,69,61,69,60,78,74,73,84,60,63,65,68,77,64,79,75,43,70,52,73,73,71,63,72,75,69,48,80,87,63,73,61,71,66,77,60,75,51,63,79,71,74,66,73,70,63,98,47,82,52,51,43,41,71,61,46,67,99,65,92,80,55,44,54,63,94,88,70,76,45,71,46,84,52,91,98,97,94,59,74,72,84,54,46,45,87,44,88,46,61,92,53,41,65,66,91,46,97,96,42,96,79,80,54,60,47,67,59,49,92,80,41,92,50,59,74,93,72";
var oArr=webTJ.getArr(oStr,",");
var oMode=webTJ.Formula.getMode(oArr);
webTJ.display("众数 = "+oMode,0);
II、组距式样本众数 [返回]
若所掌握的样本是组距式数列,则只能按一定的方法来推算众数的近似值。计算过程为:
a.根据分组频数确定众数所在组(频数最大为众数组);
b.众数所在组下限值为、上限值为,次数(频数)为D;
c.计算众数所在组次数与其下限的邻组次数之差和众数所在组次数与其上限的邻组次数之差。
众数估计公式为,
下限公式:
上限公式:
案例十:根据案例六数据,计算50名工人日加工零件数的众数。
| 按零件数分组(个) | 频数(人) |
|---|---|
| 105-110 | 3 |
| 110-115 | 5 |
| 115-120 | 8 |
| 120-125 | 14 |
| 125-130 | 10 |
| 130-135 | 6 |
| 135-140 | 4 |
解、众数所在组频数为14,下限值120、上限值125、组距为5。
下限公式:
上限公式:
计算结果,众数为123(个)。
函数代码
## 函数
webTJ.Formula.getGMode(arrs);
##参数
【arrs】
【二维数组】
代码样例
webTJ.clear();
var oArrs = [[105,110,3],[110,115,5],[115,120,8],[120,125,14],[125,130,10],[130,135,6],[135,140,4]];
var oGMode=webTJ.Formula.getGMode(oArrs);
webTJ.display("组距式分组众数 = "+oGMode,0);
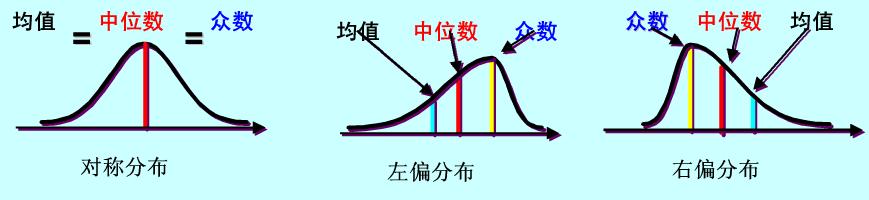
众数、中位数和算术平均数之间的关系:
众数、中位数和算术平均数都是反映总体集中趋势一般水平的指标,但三者的特点不同。样本数据中的极端值算数平均数有直接影响,对众数和中位数则无影响。用统一样本数据计算三者,其关系如下:
I、当数据具有单一众数且频数分布完全对称时,三者相同,即
此时样本数据为正态分布。
II、当出现较大极端值时,拉动算数平均数偏向数轴右方,则三者关系为,
即右偏分布时算数平均数大于众数。
III、当出现较小极端值时,拉动算数平均数偏向数轴左方,则三者关系为,
即左偏分布时算数平均数小于众数。
次数分布的非对称程度越大,三者的差别越大、反之越小。但中位数始终处于中间位置。根据皮尔逊的估计,在轻微偏态情况下,算数平均数与中位数的距离约为算数平均数与众数距离的。即,
二、变异指标统计函数###
统计变异指标又称离中趋势或离散程度指标,用来反映样本数据分布的离散程度,即反映各样本值偏离其中心值(平均数)的程度。
离散指标的作用:
评价平均指标代表性的尺度。平均指标作为总体各单位标志值一般水平的代表值,其代表性的高低取决于总体各单位标志值的差异程度。一般来说,标志值的分布越分散,离散指标值越大,平均指标的代表性就越小;标志值的分布越集中,离散指标值越小,平均数的代表性就越大;
离散指标是反映社会经济活动过程均衡性的一个重要指标。一般来说,离散指标值愈小,则说明社会经济活动过程愈均衡;离散指标值愈大,则说明社会经济活动过程存在陡起陡落的现象,需要加以调控。
测度标志变异程度的具体指标有全距、分位差、平均差、标准差等。
1、全距(Range) [返回]
全距是用来表示样本数据中的变异程度的统计量,其值为最大值与最小值之间的差距,即最大值减最小值后所得值。全距也称为极差,是指总体各单位的两个极端标志值之差,即:R=最大标志值-最小标志值。因此,全距(R)可反映总体标志值的差异范围。
案例十一:根据案例一,某学校学生英语成绩数据,
95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88
计算全距。
解、、、
函数代码
## 函数
webTJ.Formula.getRange(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oRange=webTJ.Formula.getRange(oArr);
webTJ.display("全距 = "+oRange,0);
2、平均差(Mean Deviation) [返回]
平均差是总体各单位标志对其算术平均数的离差绝对值的算术平均数。它综合反映了总体各单位标志值的变动程度。平均差越大,则表示标志变动度越大,反之则表示标志变动度越小。
在样本未分组的情况下,平均差的计算公式为:
采用标志值对算术平均数的离差绝对值之和,是因为各标志值对算术平均数的离差之代数和等于零。以几名学生数学成绩为例:
60,70,80,90,100
计算平均差如下:
函数代码
## 函数
webTJ.Formula.getMD(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oMD=webTJ.Formula.getMD(oArr);
webTJ.display("平均差 = "+oMD,0);
样本分组的情况下,平均差的计算公式为:
式中,为组数,为分组加权平均数。
案例十二:现有50名工人日加工零件数如下表,
| 按零件数分组(个) | 频数(人) | 组中值 |
|---|---|---|
| 105-110 | 3 | 107.5 |
| 110-115 | 5 | 112.5 |
| 115-120 | 8 | 117.5 |
| 120-125 | 14 | 122.5 |
| 125-130 | 10 | 127.5 |
| 130-135 | 6 | 132.5 |
| 135-140 | 4 | 137.5 |
计算分组数据平均差。
代码样例
webTJ.clear();
var oArrs = [[107.5,3],[112.5,5],[117.5,8],[122.5,14],[127.5,10],[132.5,6],[137.5,4]];
var oSrr=webTJ.Array.getMonomial(oArrs);
var oMD=webTJ.Formula.getMD(oSrr);
webTJ.display("平均差 = "+oMD,0);
注:可将组距式样本按组中值转化为单项式样本,然后利用单项式公式计算
3、四分位差(Quartile Deviation) [返回]
四分位差又称内距、也称四分间距(Inter-Quartile Range),是指将各个样本值按大小顺序排列,然后将此数列分成四等份,所得第三个四分位上的值与第一个四分位上的值的差。四分位差反映了中间50%数据的离散程度。四分位差是上四分位数()和下四分位数()之差,记为,即,
案例十三:现有200名学生统计学成绩如下(案例十三数据):
57,45,74,96,71,65,54,60,88,92,45,41,61,59,72,44,67,68,77,48,85,70,70,55,96,47,44,99,93,49,62,77,62,65,68,64,69,64,52,43,99,60,74,70,70,75,79,78,67,75,88,70,62,76,77,63,73,70,41,54,98,78,74,66,70,76,63,76,66,99,63,61,65,70,73,74,60,71,61,42,93,72,69,61,69,60,78,74,73,84,60,63,65,68,77,64,79,75,43,99,52,73,73,71,63,72,75,69,48,80,87,63,73,61,71,66,77,60,75,51,63,79,71,74,66,73,70,63,98,47,82,52,51,43,41,71,61,46,67,99,65,92,80,55,44,54,63,94,88,70,76,45,71,46,84,52,91,98,97,94,59,74,72,84,54,46,45,87,44,88,46,61,92,53,41,65,66,91,46,97,96,42,96,79,80,54,60,47,67,59,49,92,80,41,92,50,59,74,93,72
计算四分位差。
函数代码
## 函数
webTJ.Formula.getIQR(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="57,45,74,96,71,65,54,60,88,92,45,41,61,59,72,44,67,68,77,48,85,70,70,55,96,47,44,99,93,49,62,77,62,65,68,64,69,64,52,43,99,60,74,70,70,75,79,78,67,75,88,70,62,76,77,63,73,70,41,54,98,78,74,66,70,76,63,76,66,99,63,61,65,70,73,74,60,71,61,42,93,72,69,61,69,60,78,74,73,84,60,63,65,68,77,64,79,75,43,99,52,73,73,71,63,72,75,69,48,80,87,63,73,61,71,66,77,60,75,51,63,79,71,74,66,73,70,63,98,47,82,52,51,43,41,71,61,46,67,99,65,92,80,55,44,54,63,94,88,70,76,45,71,46,84,52,91,98,97,94,59,74,72,84,54,46,45,87,44,88,46,61,92,53,41,65,66,91,46,97,96,42,96,79,80,54,60,47,67,59,49,92,80,41,92,50,59,74,93,72";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oIQR=webTJ.Formula.getIQR(oArr);
webTJ.display("四分位差 = "+oIQR,0);
4、方差(Variance)和样本方差(Sample Variance) [返回]
方差是各个数据与其算术平均数的离差平方和的平均数,通常以表示。方差是一组数值和平均值分散程度的一种度量,是评价数据变异程度的标准方法。一个较大的方差,代表大部分的数值和其平均值之间差异较大;一个较小的方差,代表这些数值较接近平均值。例如,两组样本 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二组样本波动较小,具有较小的方差。
方差公式:
样本方差公式:
当根据样本推断总体方差时,样本方差为无偏估计量。统计学中另外一对常用离散程度指标是标准差(Standard Deviation)和样本标准差(Sample Standard Deviation),它们分别是方差和样本方差的平方根。
函数代码
## 函数
webTJ.Formula.getVariance(arr,k);
##参数
【arr,k】
【一维数组,方差(k=0)或样本方差(k=1)】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oS1=webTJ.Formula.getVariance(oArr,0);
webTJ.display("方差 = "+oS1,0);
var oS2=webTJ.Formula.getVariance(oArr,1);
webTJ.display("样本方差 = "+oS2,0);
var oS3=Math.pow(oS1,0.5);
webTJ.display("标准差 = "+oS3,0);
var oS4=Math.pow(oS2,0.5);
webTJ.display("样本标准差 = "+oS4,0);
5、标准差(Standard Deviation)和样本标准差(Sample Standard Deviation) [返回]
函数代码
## 函数
webTJ.Formula.getSD(arr,k);
##参数
【arr,k】
【一维数组,标准差(k=0)或样本标准差(k=1)】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oS1=webTJ.Formula.getSD(oArr,0);
webTJ.display("标准差 = "+oS1,0);
var oS2=webTJ.Formula.getSD(oArr,1);
webTJ.display("样本标准差 = "+oS2,0);
样本方差为总体方差的无偏估计量:
证明,
(证毕)
6、变异系数
变异系数又称离散系数,主要用于比较不同水平的样本数列的离散程度及平均数的代表性。变异系数是衡量数据中各观测值变异程度的一个统计量。当进行两个或多个资料变异程度的比较时,由于样本数量等级、单位不同,比较其变异程度就不能采用标准差,而需采用标准差与平均数的比值(相对值)来比较。
I、极差(全距)系数(Coefficient of Range) [返回]
全距与算数平均数之比,公式为,
函数代码
## 函数
webTJ.Formula.getVR(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oVR=webTJ.Formula.getVR(oArr,0);
webTJ.display("全距系数 = "+oVR,0);
II、平均差系数(Coefficient of Average Deviation) [返回]
平均差与算数平均数之比,公式为,
函数代码
## 函数
webTJ.Formula.getVMD(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oVMD=webTJ.Formula.getVMD(oArr,0);
webTJ.display("平均差系数 = "+oVMD,0);
III、标准差系数(Coefficient of Standard Deviation) [返回]
标准差与算数平均数之比,公式为,
函数代码
## 函数
webTJ.Formula.getVSD(arr);
##参数
【arr】
【一维数组】
一阶中心矩(k=1)等于0、二阶中心矩(k=2)为方程。
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oVSD=webTJ.Formula.getVSD(oArr,0);
webTJ.display("标准差系数 = "+oVSD,0);
三、形态指标统计函数###
集中趋势和离散趋势是数据分布的两个重要特征,但要进一步全面了解数据分布的特点,还需要知道数据分布形态是否对称、偏斜的程度以及形态的扁平程度等。
1、偏态分布(Skewed Distribution)
偏态分布,即统计数据峰值与平均值不相等的频率分布。根据峰值小于或大于平均值可分为正偏函数和负偏函数,其偏离的程度可用偏态系数刻画。偏态分布是指样本频数分布不对称。频数分布有正态分布和偏态分布之分。正态分布是指多数频数集中在中央位置,两端的频数分布大致对称。
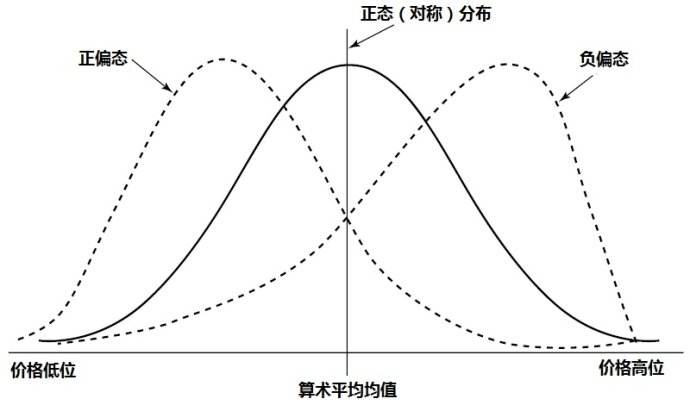
频数分布有正态分布和偏态分布之分。正态分布是指多数频数集中在中央位置,两端的频数分布大致对称。偏态分布是指频数分布不对称,如果频数分布的高峰向左偏移,长尾向右侧延伸称为正偏态分布,也称右偏态分布;同样的,如果频数分布的高峰向右偏移,长尾向左延伸则成为负偏态分布,也称左偏态分布。
I、皮尔逊偏态系数(Pearson Skewness Coefficient) [返回]
英国统计学家皮尔逊观察到算数平均数和众数、中位数的分布规律,并利用平均数和众数的关系来测定偏态,即算数平均数与众数的差距越大,次数分布的对称程度越小、偏度越大。皮尔逊将算数平均数()与众数()的差与标准差()进行对比,得到具有可比性的皮尔逊偏态系数,用来描述分布偏态的相对水平,其公式为,
一般情况下,,并且,
a. ,对称分布(实际分析时接近于0,在0.01或0.05范围内);
b. ,数据分布为左偏,或为负偏。为极度左偏;
c. ,数据分布为右偏,或为正偏。为极度右偏。
函数代码
## 函数
webTJ.Formula.getPKewness(arr);
##参数
【arr】
【一维数组】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oPSkewness=webTJ.Formula.getPSkewness(oArr);
webTJ.display("皮尔逊偏态系数 = "+oPSkewness,0);
II、原点矩(Origin Moment) [返回]
矩函数又称动差,指各样本值与某一固定值的离差的k次方的算数平均数(k阶矩),也成为与的k次动差,或称为矩函数。统计学中常用的矩函数有原点矩和中心距两种。
原点矩是指各样本值和原点的离差的k阶平均数动差,即时,k阶矩就成为k阶原点矩。公式为,
函数代码
## 函数
webTJ.Formula.getMOM(arr,k);
##参数
【arr,k】
【一维数组,k阶矩】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oMOM=webTJ.Formula.getMOM(oArr,2);
webTJ.display("原点矩 = "+oMOM,0);
III、中心矩(Central Moment) [返回]
中心矩是指各样本值与其算数平均数的离差的k阶动差的平均数,即时,k阶矩就成为k阶中心矩。公式为,
函数代码
## 函数
webTJ.Formula.getMCM(arr,k);
##参数
【arr,k】
【一维数组,k阶矩】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oMCM=webTJ.Formula.getMCM(oArr,2);
webTJ.display("原点矩 = "+oMCM,0);
IV、动差偏态系数 [返回]
利用样本的三阶中心动差与标准差三次方的比值来反映数据分布的偏态。公式为,
注:统计教课书通常采用此公式
无偏估计公式为,
注:EXCEL等软件采用此公式
当时,次数分布为对称分布;当,次数分布为右偏分布;当,次数分布为左偏分布。
函数代码
## 函数
webTJ.Formula.getSkewness(arr,k);
##参数
【arr,k】
【一维数组,有偏估计(k=0)、无偏估计(k=1)】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oSkewness=webTJ.Formula.getSkewness(oArr,0);
webTJ.display("动差偏态系数 = "+oSkewness,0);
2、峰度(Kurtosis) [返回]
峰度是指样本分布次数曲线顶峰的尖平程度,是次数分布的又一重要特征。统计上,常以正态分布曲线为标准,来观察比较某一次数分布曲线的顶端为尖顶或平顶以及尖平程度的大小。
峰度的测定,一般是采用统计动差方法,即以四阶中心动差为测定依据,将除以其标准差的四次方(),以消除单位量纲的影响,便于不同次数分布曲线的峰度比较,从而得到以量纲表示的相对数,即为峰度的测定值。计算公式为:
注:统计教课书通常采用此公式
由统计计算分析可知,当次数分布为正态分布曲线时,,以此为标准就可比较分析各种次数分布曲线的峰度。当时,表示分布曲线呈尖顶峰度,为尖顶曲线,说明变量值的次数较为密集地分布在众数的周围,值越大于3,分布曲线的顶端越尖峭。当时,表示分布曲线呈平顶峰度,为平顶曲线,说明变量值的次数分布比较均匀地分散在众数的两侧,值越小于3,则分布曲线的顶峰就越平缓。一般当值接近于1.8时,分布曲线呈水平矩形分布形态,说明各组变量值的次数相同。当值小于1.8时,次数分布曲线趋向“U”型分布。实际统计分析中,通常将偏度和峰度结合起来运用,以判断变量分布是否接近于正态分布。
峰度的无偏估计公式为,
注:EXCEL等软件采用此公式,峰度判别标准由3调整为0

函数代码
## 函数
webTJ.Formula.getKurtosis(arr,k);
##参数
【arr,k】
【一维数组,有偏估计(k=0)、无偏估计(k=1)】
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oKurtosis=webTJ.Formula.getKurtosis(oArr,0);
webTJ.display("峰度系数 = "+oKurtosis,0);
四、在线数据操作练习###
1、字符串转数组后,应先进行量化后再计算各项统计指标
设有学生成绩字符串数据如下:
95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88
计算标准差。
代码样例
webTJ.clear();
var oStr="95,74,31,68,50,68,59,33,41,33,81,53,91,68,35,57,58,63,77,62,62,92,37,36,87,88,86,88,47,91,51,41,82,82,63,86,90,43,31,57,73,41,50,97,83,85,38,70,61,90,53,71,42,59,41,99,63,86,55,95,31,37,65,48,93,51,63,47,92,95,39,44,93,96,85,33,95,47,34,56,70,93,60,88,34,43,98,70,56,73,78,82,40,57,61,53,49,60,94,88";
var oArr=webTJ.getArr(oStr,",");
oArr=webTJ.Array.getQuantify(oArr);
var oVSD=webTJ.Formula.getVSD(oArr,0);
webTJ.display("标准差系数 = "+oVSD,0);
注:字符串转换为数组后,运用数组类函数的getQuantify函数将数组量化后再进行统计计算。如果没有量化过程可能无法返回正确计算结果
2、单项式和组距式分组数据数组定义
某工厂工人产量单项式分组数据表(产量表)如下:
| 日产量分组(件) | 工人数(个) |
|---|---|
| 4 | 8 |
| 5 | 22 |
| 6 | 42 |
| 7 | 38 |
| 8 | 17 |
| 9 | 3 |
另有100名学生英语成绩组距式分组表(成绩表)如下,
| 下限 | 上限 | 组中值 | 权数 |
|---|---|---|---|
| 30 | 40 | 35 | 14 |
| 40 | 50 | 45 | 14 |
| 50 | 60 | 55 | 16 |
| 60 | 70 | 65 | 14 |
| 70 | 80 | 75 | 9 |
| 80 | 90 | 85 | 15 |
| 90 | 100 | 95 | 18 |
将两表中数据定义为数组,并计算加权算术平均数。
注:单项式和组距式分组数据应定义为二维数组。单项式数组数据第一列为单项数值,第二列为分组次数;组距式数组数据第一列为各组组中值,第二列也为分组次数
代码样例
webTJ.clear();
var oArrs1=[[4,8],[5,22],[6,42],[7,38],[8,17],[9,3]]; //定义成绩表数组
var oWMean1=webTJ.Formula.getWMean(oArrs1);
webTJ.display("产量表加权算术平均数 = "+oWMean1,0);
var oArrs2=[[35,14],[45,14],[55,16],[65,14],[75,9],[85,15],[95,18]]; //定义产量表数组
var oWMean2=webTJ.Formula.getWMean(oArrs2);
webTJ.display("成绩表加权算术平均数 = "+oWMean2,0);
3、分组数据统计指标可转换为单项式后,用单项式统计公式
根据下表计算50名工人日加工零件数的方差和众数。
| 按零件数分组(个) | 频数(人) |
|---|---|
| 105-110 | 3 |
| 110-115 | 5 |
| 115-120 | 8 |
| 120-125 | 14 |
| 125-130 | 10 |
| 130-135 | 6 |
| 135-140 | 4 |
注:通常数据有单项和分组两种形式,如果只有单项式统计公式,可先将分组数据转换为单项式数据后按单项式公式计算
代码样例
webTJ.clear();
var oArrs=[[107.5,3],[112.5,5],[117.5,8],[122.5,14],[127.5,10],[132.5,6],[137.5,4]];
//按组中值定义组距式数组
var oSrr=webTJ.Array.getMonomial(oArrs); //根据权数将分组样本转换为单项式
webTJ.display(oSrr,0);
var oVar=webTJ.Formula.getVariance(oSrr,0); //计算方差
webTJ.display("方差 = "+oVar,0);
var oMode=webTJ.Formula.getMode(oSrr); //按单项式计算众数
webTJ.display("单项式众数 = "+oMode,0);
var oArrs = [[105,110,3],[110,115,5],[115,120,8],[120,125,14],[125,130,10],[130,135,6],[135,140,4]];
//按上限和下限定义组距式数组
var oGMode=webTJ.Formula.getGMode(oArrs); //按组距式计算众数
webTJ.display("组距式众数 = "+oGMode,0);
注:运用组距式分组数据计算中位数和众数时需要用分组上限和下限计算组距,应按上限和下限定义组距式数组
代码窗口
注:可将例题实例代码复制、粘贴到“代码窗口”,点击“运行代码”获得计算结果(鼠标选择实例代码Ctrl+C:复制鼠标点击“代码窗口”使其获得焦点Ctrl+V:粘贴)
运行效果
银河统计工作室成员由在校统计、计算机部分师生和企业数据数据分析师组成,维护和开发银河统计网和银河统计博客(技术文档)。专注于数据挖掘技术研究和运用,探索统计学、应用数学和IT技术有机结合,尝试大数据条件下新型统计学教学模式。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架