统计数据模拟及其运用

（2017-02-23 银河统计）

统计数据模拟指以统计和数学算法为基础、运用计算机软件大量生成合理的、接近于自然、社会现象实际数量、质量指标的样本，从而大数据仿真样本建立各种估计量或技术各种统计指标。

1、数据模拟概述

统计数据模拟分为确定型数据模拟和随机型数据模拟。统计数据模拟解决问题基本分为三个部分：建立模型、生成样本、参数估算。

确定型数据模拟

确定型数据模拟是在所研究的自然、社会现象数量、质量指标的值域或定义域范围内运用计算机软件编程技术生成全部解样本或可行解样本，进而根据样本通过大量运算获得问题的最优或近似解。这就是所谓计算机“海算”或“傻瓜”算法。虽然目前计算机运算速度和容量已经很快、很大，但面对很多复杂问题、特别是多变量组合样本，生成并计算全部样本往往受到限制（在网页中进行模拟运算更是如此）。生成全部解样本或可行解样本需要集合论、组合数学等知识，这样才能确定运算范围和减少运算量。

统计指标：统计指标简称指标，是反映自然、社会经济现象总体综合数量特征的范畴及其具体数值。如我国人口总数为13亿、土地面积960万平方公里等都属于统计指标。统计指标由两个基本要素构成，即指标名称和指标数值。除了这两个基本要素外，还应有时间限制、空间限制、统计方法和计量单位等四个要素。统计指标是一种统计结果，是反映确定统计对象的综合数量特征的概念及其具体数值。

统计数量指标：是反映总体（所研究事物的全体）绝对量多少或规模大小的统计指标，常用总量数值的形式来表示，也称为总量指标。如人口数、商品销售额等。

统计质量指标：是反映自然、社会经济现象相对水平或平均水平（相对数或平均数）的统计指标，如劳动生产率、单位面积产量、单位产品成本、设备利用率等。质量指标的计算和分析对挖掘各部门、各单位工作中的内部潜力具有重要作用。

随机型数据模拟

随机型数据模拟是将所研究的自然、社会现象作为随机现象来处理，而自然、社会现象的数量、质量指标为随机变量。一般情况下，统计数据模拟泛指随机型数据模拟。

统计随机型数据模拟，又称随机抽样或统计试验方法，即大名鼎鼎的蒙特卡罗（Monte Carlo）方法，属于计算数学的一个分支。它是在上世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。

当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

随机型数据模拟需要坚实的概率和数理统计知识，特别是对常用随机分布模型及数据特征、性质和适应范围有深入理解。

2、确定型数据模拟案例

**I、解一元方程##\(x^2-9=0\)

a. 运用步长法解方程

样本范围：解一元方程属于纯数学问题，如果没有什么统计限制，一般情况下解的范围可能为$\pm\infty$，这显然超出计算机模拟或计算范围。好在统计数据不同于纯数学数据，统计数据根据实际经验人们会给出合理范围或经验值域。例如，人类的身高和体重范围。尽管很难说出最大、最小值，但身高在肯定不会超出5-300cm，这样计算机就有用武之地了。

方程\(x^2-9=0\)的解为\(\pm3\)，可以在\(\pm10\)范围内取样。

样本密度：在确定型数据模拟过程中，确定样本范围后面临在样本范围内的取样密度问题。如在数值5-300内按不同间距取样，取样步长越小、样本量越大，样本密度越高。

在\(\pm10\)范围，步长为1，方程\(x^2-9=0\)的自变量取21个样本。步长为0.1取201个样本，步长为0.01取2001个样本，...。

步长法：当问题维数（变量）较少时、或样本密度较低时，根据解的范围适当确定步长，通过运算缩小解的范围，在小范围内进一步缩小步长，直至达到精度要求。穷举法可以看做是在一定范围内获取全部样本。
步长法第一轮计算（步长=1）
kxf(x)
10.55-8.6975
21.55-6.5975
32.55-2.4975
43.553.6025
54.5511.7025
65.5521.8025
76.5533.9025
87.5548.0025
98.5564.1025
109.5582.2025
1110.55102.3025
注：由于方程在0-10范围内，$x=3$为方程的解，取步长为1时可以幸运地在第一轮计算中得到精确解。为展示一般计算过程，将搜索范围改为0.55-10.55。通过第一轮计算搜索范围缩小为2.55-3.55，缩小步长为0.1继续搜索计算

步长法第二轮计算（步长=0.1）
kxf(x)
12.55-2.4975
22.65-1.9775
32.75-1.4375
42.85-0.8775
52.95-0.2975
63.050.3025
73.150.9225
83.251.5625
93.352.2225
103.452.9025
113.553.6025
注：通过第二轮计算搜索范围缩小为2.95-3.05，缩小步长为0.01继续搜索计算

步长法第三轮计算（步长=0.01）
kxf(x)
12.95-0.2975
22.96-0.2384
32.97-0.1791
42.98-0.1196
52.99-0.0599
630
73.010.0601
83.020.1204
93.030.1809
103.040.2416
113.050.3025
注：通过第三轮计算，得方程解为$x=3$

b. 运用二分法解方程

二分法：在确定样本范围值的中点取样，判断解的位置在中点的左边，舍去右半边，再在左半边取中点进行判断、取舍，直至逼近问题的解。二分法可以看做是按变量范围中点进行条件判断取样，或称为条件抽样。

如方程\(x^2-9=0\)解的范围为\(\pm10\)，运用二分法自变量取样的第一个中点为0，将自变量两端和中点值带入方程\(f(x)=x^2-9\)得，

\[\begin{equation*} \begin{cases} f(-10)=-10^2-9=91\\ f(0)=0^2-9=-9\\ f(10)=10^2-9=91\\ \end{cases} \end{equation*} \]

由于自变量从\(f(-10)\)和\(f(0)\)正负号异号，说明-10-0范围内有解。同理，0-10范围内有另一个解。

二分法解的收敛计算过程表（$0\le x\le 10$）
kx1xx2f(x1)f(x)f(x2)
10.0000005.00000010.000000-9.00000016.00000091.000000
20.0000002.5000005.000000-9.000000-2.75000016.000000
32.5000003.7500005.000000-2.7500005.06250016.000000
42.5000003.1250003.750000-2.7500000.7656255.062500
52.5000002.8125003.125000-2.750000-1.0898440.765625
62.8125002.9687503.125000-1.089844-0.1865230.765625
72.9687503.0468753.125000-0.1865230.2834470.765625
82.9687503.0078133.046875-0.1865230.0469360.283447
92.9687502.9882813.007813-0.186523-0.0701750.046936
102.9882812.9980473.007813-0.070175-0.0117150.046936
112.9980473.0029303.007813-0.0117150.0175870.046936
122.9980473.0004883.002930-0.0117150.0029300.017587
132.9980472.9992683.000488-0.011715-0.0043940.002930
142.9992682.9998783.000488-0.004394-0.0007320.002930
152.9998783.0001833.000488-0.0007320.0010990.002930
162.9998783.0000313.000183-0.0007320.0001830.001099
172.9998782.9999543.000031-0.0007320.0002750.000183
182.9999542.9999923.000031-0.000275-0.0000460.000183
192.9999923.0000113.000031-0.0000460.0000690.000183
202.9999923.0000023.000011-0.0000460.0000110.000069
212.9999922.9999973.000002-0.000046-0.0000170.000011
222.9999973.0000003.000002-0.000017-0.0000030.000011
注：$k=1$，左端点$x_1=0$、右端点$x_2=10$、中点$x=5$，因为$f(0)=-9$、$f(5)=16$（正负号异号），下一轮计算左右端点为0、5，中点为2.5，以后各轮计算同理。

II、搬砖问题

男人、女人和小孩一起搬砖，其中男人一次能搬4块转、女人2块、4个小孩搬1块。要求每类人都要参加搬砖，100个人搬100块砖，需要多少男人、女人和小孩？

解：设男人为M、女人为F、小孩为C。根据题意有，

\[\begin{equation*} \begin{cases} M+F+C=100\\ 4M+2F+\frac{C}{4}=100\\ \end{cases} \end{equation*} \]

由于人数为正整数，每类人都必须参加搬砖，容易判定出\(M\ge 1\)、\(F\ge 1\)、\(C\ge 8\)。通过分析可知，男人数达到20时无论怎样安排女人和小孩，搬砖数达100时都无法凑够人数。所以，\(M < 20\)；同样容易判定出\(F \le 47\)、\(C \le 72\)。男人、女人和小孩三个整数变量值域为，

\[\begin{equation*} \begin{cases} 1 \le M \le 19\qquad [1,2,3,\dots,19]\\ 1 \le F \le 47\qquad [1,2,3,\dots,47]\\ 8 \le C \le 72\qquad [8,12,16,\dots,72]\\ \end{cases} \end{equation*} \]

可行解样本数为\(19\times47\times(18-1)=19\times47\times17=15181\)。无论男人和女人为多少搬砖的总数为偶数，小孩的人数为8的倍数才可能凑齐偶数100块砖，即小孩的人数可以缩小为数据集[8,16,24,32,40,48,56,64,72]。进一步仔细分析男人和女人可能数据范围，可行解样本总量还会进一步缩小。

搬砖问题代码样例：

webTJ.clear();
var oArrs=[];
var oCount=0;
var oID=0;
var oTBList="<table style='width:90%; font-size:9pt;'>";
oTBList+="<caption>搬砖问题可行解样本表</caption>";
oTBList+="<tr><th>No.</th><th>男人</th><th>女人</th><th>小孩</th><th>人数</th><th>砖数</th></tr>";
for (var i=1; i<=19; i++) {
  for (var j=1; j<=47; j++) {
    for (var k=2; k<=18; k++) {
      oCount++;
      oTBList+="<tr><td>"+oCount+"</td><td>"+i+"</td><td>"+j+"</td><td>"+4*k+"</td><td>"+(i+j+4*k)+"</td><td>"+(4*i+2*j+k)+"</td></tr>";
      if (i+j+4*k==100 && 4*i+2*j+k==100) {
        oArrs[oID]=[];
        oArrs[oID][0]=i; oArrs[oID][1]=j; oArrs[oID][2]=4*k;
        oID++;
        }
      }
    }
  }
  oTBList+="</table>";
  webTJ.display("可行解样本数："+oCount,0);
  var oLen=oArrs.length;
  webTJ.display("问题共有"+oLen+"组答案",0);
  var oTB="<table style='width:90%'>";
  oTB+="<caption>搬砖问题答案表</caption>";
  oTB+="<tr><th>No.</th><th>男人</th><th>女人</th><th>小孩</th></tr>";
  for (var i=0; i<oLen; i++) {
    oTB+="<tr><td>"+(i+1)+"</td><td>"+oArrs[i][0]+"</td><td>"+oArrs[i][1]+"</td><td>"+oArrs[i][2]+"</td></tr>";
    }
  oTB+="</table>";
  webTJ.display(oTB,0);
  webTJ.display(oTBList,0);
注：如果目的只是关心问题的解，没必要输出可行解样本表，计算速度会更快。当数据计算量较大时，尽量不要在表格或其它网页插件中输出数据，这样会大大降低数据处理效率。计算过程中需要存储大数据时，尽量将数据临时储存在数组中

如果不考虑输出可行解样本表，脚本代码运行速度将大大提高。改进的搬砖问题代码样例：

webTJ.clear();
var oArrs=[];
var oCount=0;
var oID=0;
for (var i=1; i<=19; i++) {
  for (var j=1; j<=47; j++) {
    for (var k=2; k<=18; k++) {
      oCount++;
      if (i+j+4*k==100 && 4*i+2*j+k==100) {
        oArrs[oID]=[];
        oArrs[oID][0]=i; oArrs[oID][1]=j; oArrs[oID][2]=4*k;
        oID++;
        }
      }
    }
  }
  webTJ.display("可行解样本数："+oCount,0);
  var oLen=oArrs.length;
  webTJ.display("问题共有"+oLen+"组答案",0);
  var oTB="<table style='width:90%'>";
  oTB+="<caption>搬砖问题答案表</caption>";
  oTB+="<tr><th>No.</th><th>男人</th><th>女人</th><th>小孩</th></tr>";
  for (var i=0; i<oLen; i++) {
    oTB+="<tr><td>"+(i+1)+"</td><td>"+oArrs[i][0]+"</td><td>"+oArrs[i][1]+"</td><td>"+oArrs[i][2]+"</td></tr>";
    }
  oTB+="</table>";
  webTJ.display(oTB,0);

III、掷色子问题

同时掷\(N\)(\(N=2,3,4,\dots\))个色子，点数之和为\(S\)(\(N \le S \le 6\times N\))，点数之和为多少时概率最大？

解：

a. \(N=1\)，共有6种可能样本，\(1 \le S \le 6\)，1-6点发生概率相等，为1/6。试验样本如下表：

样本123456
注：掷一个色子的结果为一维随机变量，样本为一行或一列

b. \(N=2\)，共有\(6^2=36\)种可能样本，点数和S值域\(2 \le S \le 12\)，试验样本如下表：

样本123456
1234567
2345678
3456789
45678910
567891011
6789101112
注：掷两个色子的结果为二维随机变量，样本为$6\times6$二维平面表

表中对角线为7，发生次数最多为6次。所以，

\[P(S=7)=\frac{6}{36}=\frac{1}{6} \]

\(N=2\)时，点数之和S发生次数(N)和概率(P)分布表为，

S23456789101112$\Sigma$
N1234565432136
P$\frac{1}{36}$$\frac{2}{36}$$\frac{3}{36}$$\frac{4}{36}$$\frac{5}{36}$$\frac{6}{36}$$\frac{5}{36}$$\frac{4}{36}$$\frac{3}{36}$$\frac{2}{36}$$\frac{1}{36}$1
注：掷两个色子的样本可以用1张$6\times6$二维平面表来描述，第一行和第一列为两个色子点数，交叉点为两个色子点数之和

c. \(N=3\)，共有\(6^3=216\)种可能样本，点数和S值域\(3 \le S \le 18\)，三个色子点数和试验样本如下，

第3个色子为1
345678
456789
5678910
67891011
789101112
8910111213
第3个色子为2
456789
5678910
67891011
789101112
8910111213
91011121314
第3个色子为3
5678910
67891011
789101112
8910111213
91011121314
101112131415
第3个色子为4
67891011
789101112
8910111213
91011121314
101112131415
111213141516
第3个色子为5
789101112
8910111213
91011121314
101112131415
111213141516
121314151617
第3个色子为6
8910111213
91011121314
101112131415
111213141516
121314151617
131415161718
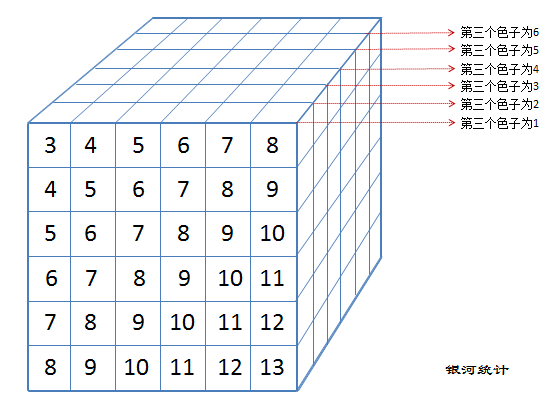注：掷三个色子的样本可以用6张$6\times6$二维平面表来描述 注：掷三个色子的样本可以进一步用一个$6\times6\times6$三维数据立方来描述

d. \(N=4\)，共有\(6^4=1296\)种可能样本，点数和S值域\(4 \le S \le 24\)。

随着掷色子数量的增加，可能样本数量呈几何递增，掷色子数量超过10个，样本数量超过亿，如下表，

色子234567891011
样本量36216129677764665627993616796161007769660466176362797056
注：掷11个色子的样本数量迅速上升为3亿6千多万

当色子较多时，无法用一般计算机模拟计算全部样本空间，此时需要数学算法给出结构表达式，在辅以计算机算法来解决问题。“算法为王”！

同时掷1个色子（\(N=1\)），样本空间为一个“数据链”；
同时掷2个色子（\(N=2\)），样本空间为一个“数据面”；
同时掷3个色子（\(N=3\)），样本空间为一个“数据立方”；

同时掷3个以上色子（\(N\ge 3\)），样本空间成为超空间，其具体形态已超出我们的想象。根据前面分析可知，同时掷三个色子的样本空间可以用6张\(6\times6\)二维平面表来描述、或用一个\(6\times6\times6\)三维数据立方来描述，这里“数据面”或“数据立方”为用低维样本空间描述高维样本空间的基本数据面和数据块，三维以上样本空间可以选用基本数据面或数据块来描述。

例如同时掷4个色子（\(N=4\)），样本空间由6个数据立方组成（基本数据立方为掷3个色子产生的数据立方，简称“基本方”），每个基本方（由6个数据面216个数字构成）所有数字分别加1-6。

同时掷4个色子（\(N=4\)），样本空间也可由36个数据面组成（基本数据面为掷2个色子产生的数据面，简称“基本面”），每个基本面（由36个数字构成）。每个基本面分别加1-6，分解为6个数据面（同时掷3个色子的样本空间），每个数据面再分别加1-6，分解为36个数据面（同时掷4个色子的样本空间）。如此递推，可描述更高样本空间。

掷色子问题代码样例：

webTJ.clear();
var oSample={
  getZYs:function(m) {
  var n=6*m;
  var oArr=[];
  for (var i=m; i<=n; i++) {oArr[i-m]=[]; oArr[i-m][0]=i; oArr[i-m][1]=0;}
  return oArr;
  },
  getCode:function(m) {
  var oStr="";
  for (var i=1; i<=m; i++) {
    if (i<m) {oStr+="n"+i+"+";} else {oStr+="n"+i;}
    }
  oStr="oArr["+oStr+"-"+m+"][1]++;";
  var oStr1=""; var oStr2="";
  for (var i=1; i<=m; i++) {
    oStr1+="for (var n"+i+"=1; n"+i+"<=6; n"+i+"++) {";
    oStr2+="}";
    }
  oStr=oStr1+oStr+oStr2;
  return oStr;
  }
}
var oDice=4; //掷色子数
var oArr=oSample.getZYs(oDice)
var oCode=oSample.getCode(oDice);
eval(oCode);
var oLen=oArr.length;
var oSize=Math.pow(6,oDice);
for (var i=0; i<oLen; i++) {
  oArr[i][2]=Math.round(Math.pow(10,8)*oArr[i][1]/oSize)/Math.pow(10,8);
  }
webTJ.display("同时掷"+oDice+"个色子点数和发生次数和概率分布",0);
webTJ.display(oArr,1);
注：脚本中代码"var oDice=4;"设置同时掷色子数量为4，可将代码中的4改为其它正整数（建议小于9，如果数值过大容易卡死），复制、粘贴脚本到“代码窗口”、点击“运行代码”获得不同数量色子分布次数和频率（建议使用Google Chrome运行脚本，当然运算容量和速度和计算机配置有关）

在脚本中分别取oDice为\(2,3,\dots,10\)，最大点数和S及发生次数和概率表如下：

色子数量最大点数发生次数发生概率样本总数
2760.1666666736
310/11270.125216
4141460.112654321296
517/187800.000308647776
62143320.0928497946656
724/25240170.08579461279936
8281359540.08094351679616
931/327673940.0763477610077696
103543954560.0726928160466176
注：色子数大于10用脚本在浏览器上运行几乎不可能，需要C或其它语言编程计算

根据最大点数和S及发生次数和概率表，对于掷色子最大点数问题总结如下：

定义点数和S值域
最大点数和S为值域的中间数
构成点数和S值域的最小值为偶数，最大点数为值域的中位数；值域的最小值为奇数，最大点数为值域的中间的两个数
随着试验色子数量的增加，最大点数发生概率呈指数递减，色子数趋向无穷大时不知是否收敛？

例如，色子数为100时，点数和S值域为100-600，值域最小数为偶数，最大点数为该值域的中位数350。至于最大点数350的发生次数则需要大型计算机或纯数学来证明。

最大素数是多少、圆周率\(\pi\)最大小数位数等问题的根本解决需要理论数学，但大型计算机能让人们得到很多结果（计算数学家门还没完全解决这些问题），这或许可以称为“算法黑科技”。

确定型数据模拟可以归结为问题可行解样本空间算法问题，利用高效的数学算法和有限的计算机资源解决大样本空间遍历运算是技术的关键。

3、随机型数据模拟案例

由于银行统计博客中已有一些Web Service接口和随机型数据模拟案例，这里例举一个简单案例：学习成绩模拟问题。

学习成绩模拟可以考虑用正态分布、二项分布、泊松分布和按给定比例结合均匀分布来模拟产生。

I、用正态分布生成平均分数为70、标准差为15的100名学生模拟成绩

如果所需随机样本量不是太多，可直接在一个新打开页面的浏览器地址中通过Web Service接口返回样本。具体过程如下，

生成正态分布模拟样本：

A.Web Service接口: http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=normal_r&var_name=randomZT&sample_size=100&decimal_places=4&mean_value=70&sd_value=15
B.复制、粘贴接口到新打开页面浏览器地址中，运行返回样本
C.样本样例：var random_number={"result": ["52|72|78|89|57|62|76|50|77|38|52|69|66|102|97|58|58|49|62|70|86|80|56|95|54|88|69|71|79|86|78|70|77|93|70|97|94|58|82|92|71|67|90|48|80|67|82|67|67|87|65|74|79|58|72|60|64|68|42|61|62|73|66|91|94|60|80|59|76|49|79|73|77|89|61|68|72|57|77|81|77|63|94|103|86|71|112|63|81|58|62|80|77|69|66|96|54|78|44|107"]}
D.将样本变量复制、粘贴到代码窗口供编程调用

注：有正态分布生成的学习成绩有个别数据超过100分（标准差偏大），此时应按100分处理。Web Service接口参见银河统计博文统计随机数及临界值Web Service接口

正态分布模拟学生成绩和统计分组代码样例：

webTJ.clear();
var random_number={"result": ["52|72|78|89|57|62|76|50|77|38|52|69|66|102|97|58|58|49|62|70|86|80|56|95|54|88|69|71|79|86|78|70|77|93|70|97|94|58|82|92|71|67|90|48|80|67|82|67|67|87|65|74|79|58|72|60|64|68|42|61|62|73|66|91|94|60|80|59|76|49|79|73|77|89|61|68|72|57|77|81|77|63|94|103|86|71|112|63|81|58|62|80|77|69|66|96|54|78|44|107"]};
var oTxt=random_number.result[0];
var oArr=oTxt.split("|");
var oDrr=[0,0,0,0,0];
var oLen=oArr.length;
for (var i=0; i<oLen; i++) {
  if (oArr[i]>100) {oArr[i]=100;}
  if (oArr[i]<60) {oDrr[0]++;}
  if (oArr[i]>=60 && oArr[i]<70) {oDrr[1]++;}
  if (oArr[i]>=70 && oArr[i]<80) {oDrr[2]++;}
  if (oArr[i]>=80 && oArr[i]<90) {oDrr[3]++;}
  if (oArr[i]>=90 && oArr[i]<=100) {oDrr[4]++;}
  }
var oTB="<table style='width:90%; font-size:9pt;'>";
oTB+="<td>成绩-X</td><td>0-59</td><td>60-69</td><td>70-79</td><td>80-89</td><td>90-100</td><td>合计</td></tr>";
oTB+="<td>发生次数</td><td>"+oDrr[0]+"</td><td>"+oDrr[1]+"</td><td>"+oDrr[2]+"</td><td>"+oDrr[3]+"</td><td>"+oDrr[4]+"</td>    <td>100</td></tr>";
oTB+="</table>";
webTJ.display(oTB,0);

II、用二项分布生成平均分数为70的150名学生模拟成绩

生成二项分布模拟样本：

A.Web Service接口: http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=binom_r&var_name=random_number&sample_size=150&decimal_places=0&size_value=100&prob_value=0.7
B.复制、粘贴接口到新打开页面浏览器地址中，运行返回样本
C.样本样例：var random_number={"result": ["78|70|69|65|62|65|62|66|68|64|64|62|69|66|68|62|69|73|70|69|73|64|69|71|75|78|65|68|70|81|66|77|74|78|66|64|76|79|67|61|68|65|68|69|69|73|75|69|69|61|72|74|63|64|72|65|75|69|69|71|69|65|70|70|73|63|62|68|69|71|71|72|68|63|61|63|78|69|73|74|67|71|68|64|67|69|71|69|74|71|66|73|68|63|67|73|73|70|64|71|78|72|72|75|70|69|70|63|69|70|75|71|73|72|69|68|75|69|71|61|69|79|71|71|70|67|77|77|66|70|61|74|75|74|62|76|73|68|70|74|72|70|75|68|64|73|72|68|71|67"]}
D.将样本变量复制、粘贴到代码窗口供编程调用

二项分布成功概率为p，均值为np。用二项分布生成平均分数为70的150个学生成绩样本，可取prob_value=0.7（p=0.7），sample_size=150(样本数)，size_value=100（发生次数，可将样本控制在100之内）

二项分布模拟学生成绩和统计分组代码样例：

webTJ.clear();
var random_number={"result": ["78|70|69|65|62|65|62|66|68|64|64|62|69|66|68|62|69|73|70|69|73|64|69|71|75|78|65|68|70|81|66|77|74|78|66|64|76|79|67|61|68|65|68|69|69|73|75|69|69|61|72|74|63|64|72|65|75|69|69|71|69|65|70|70|73|63|62|68|69|71|71|72|68|63|61|63|78|69|73|74|67|71|68|64|67|69|71|69|74|71|66|73|68|63|67|73|73|70|64|71|78|72|72|75|70|69|70|63|69|70|75|71|73|72|69|68|75|69|71|61|69|79|71|71|70|67|77|77|66|70|61|74|75|74|62|76|73|68|70|74|72|70|75|68|64|73|72|68|71|67"]};
var oTxt=random_number.result[0];
var oArr=oTxt.split("|");
var oDrr=[0,0,0,0,0];
var oLen=oArr.length;
for (var i=0; i<oLen; i++) {
  if (oArr[i]>100) {oArr[i]=100;}
  if (oArr[i]<60) {oDrr[0]++;}
  if (oArr[i]>=60 && oArr[i]<70) {oDrr[1]++;}
  if (oArr[i]>=70 && oArr[i]<80) {oDrr[2]++;}
  if (oArr[i]>=80 && oArr[i]<90) {oDrr[3]++;}
  if (oArr[i]>=90 && oArr[i]<=100) {oDrr[4]++;}
  }
var oTB="<table style='width:90%; font-size:9pt;'>";
oTB+="<td>成绩-X</td><td>0-59</td><td>60-69</td><td>70-79</td><td>80-89</td><td>90-100</td><td>合计</td></tr>";
oTB+="<td>发生次数</td><td>"+oDrr[0]+"</td><td>"+oDrr[1]+"</td><td>"+oDrr[2]+"</td><td>"+oDrr[3]+"</td><td>"+oDrr[4]+"</td>    <td>100</td></tr>";
oTB+="</table>";
webTJ.display(oTB,0);

III、用泊松分布生成平均分数为70的150名学生模拟成绩

生成泊松分布模拟样本：

A.Web Service接口: http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=pois_r&var_name=random_number&sample_size=150&decimal_places=0&labmda_value=70
B.复制、粘贴接口到新打开页面浏览器地址中，运行返回样本
C.样本样例：var random_number={"result": ["57|76|79|66|72|72|75|79|82|74|68|71|66|83|87|65|68|70|74|84|69|75|73|69|69|73|81|72|60|71|68|75|70|68|60|68|88|60|69|67|72|64|72|75|63|70|79|80|78|60|72|76|67|71|56|75|55|55|68|60|58|74|47|63|72|81|89|61|59|79|71|75|63|65|78|69|83|66|63|64|60|70|77|74|72|81|65|71|66|79|58|69|67|82|68|81|65|64|69|69|83|68|76|70|77|62|63|68|61|73|64|70|74|66|72|63|64|64|69|67|70|92|53|59|60|75|83|67|68|66|67|87|56|66|60|68|74|68|74|67|56|73|70|79|81|72|70|78|67|78"]}
D.将样本变量复制、粘贴到代码窗口供编程调用

二项分布模拟学生成绩和统计分组代码样例：

webTJ.clear();
var random_number={"result": ["57|76|79|66|72|72|75|79|82|74|68|71|66|83|87|65|68|70|74|84|69|75|73|69|69|73|81|72|60|71|68|75|70|68|60|68|88|60|69|67|72|64|72|75|63|70|79|80|78|60|72|76|67|71|56|75|55|55|68|60|58|74|47|63|72|81|89|61|59|79|71|75|63|65|78|69|83|66|63|64|60|70|77|74|72|81|65|71|66|79|58|69|67|82|68|81|65|64|69|69|83|68|76|70|77|62|63|68|61|73|64|70|74|66|72|63|64|64|69|67|70|92|53|59|60|75|83|67|68|66|67|87|56|66|60|68|74|68|74|67|56|73|70|79|81|72|70|78|67|78"]};
var oTxt=random_number.result[0];
var oArr=oTxt.split("|");
var oDrr=[0,0,0,0,0];
var oLen=oArr.length;
for (var i=0; i<oLen; i++) {
  if (oArr[i]>100) {oArr[i]=100;}
  if (oArr[i]<60) {oDrr[0]++;}
  if (oArr[i]>=60 && oArr[i]<70) {oDrr[1]++;}
  if (oArr[i]>=70 && oArr[i]<80) {oDrr[2]++;}
  if (oArr[i]>=80 && oArr[i]<90) {oDrr[3]++;}
  if (oArr[i]>=90 && oArr[i]<=100) {oDrr[4]++;}
  }
var oTB="<table style='width:90%; font-size:9pt;'>";
oTB+="<td>成绩-X</td><td>0-59</td><td>60-69</td><td>70-79</td><td>80-89</td><td>90-100</td><td>合计</td></tr>";
oTB+="<td>发生次数</td><td>"+oDrr[0]+"</td><td>"+oDrr[1]+"</td><td>"+oDrr[2]+"</td><td>"+oDrr[3]+"</td><td>"+oDrr[4]+"</td>    <td>100</td></tr>";
oTB+="</table>";
webTJ.display(oTB,0);

IV、按给定比例结合均匀分布生成1000名学生学习成绩

不同分组学习成绩X所占比例如下表：

a. 学习成绩分组比例

成绩分组$X<60$$60\le X <70$$70\le X <80$$80\le X <90$$90\le X \le 100$合计
分组比例0.10.40.30.150.051
累计比例0.10.50.80.951*

b. 均匀分布随机数

几乎每种编程软件都可以生成0-1均匀分布，JS可以用函数Math.random()生成0-1均匀分布。生成一个0-1均匀分布样本S，如果

\(S<0.1\)、不及格计数一次
\(0.1\le S<0.5\)、60-69计数一次
\(0.5\le S<0.8\)、70-79计数一次
\(0.8\le S<0.95\)、80-89计数一次
\(0.95\le S \le 1\)、90-100计数一次。

c. 样本生成代码

按给定比例结合均匀分布生成1000名学生学习成绩代码样例：

webTJ.clear();
var oDrr=[0,0,0,0,0];
var rd;
for (var i=0; i<1000; i++) {
  rd=Math.random();
  if (rd<0.1) {oDrr[0]++;}
  if (rd>=0.1 && rd<0.5) {oDrr[1]++;}
  if (rd>=0.5 && rd<0.8) {oDrr[2]++;}
  if (rd>=0.8 && rd<0.95) {oDrr[3]++;}
  if (rd>=0.95 && rd<=1) {oDrr[4]++;}
  }
var oTB="<table style='width:90%; font-size:9pt;'>";
oTB+="<td>成绩-X</td><td>0-59</td><td>60-69</td><td>70-79</td><td>80-89</td><td>90-100</td><td>合计</td></tr>";
oTB+="<td>发生次数</td><td>"+oDrr[0]+"</td><td>"+oDrr[1]+"</td><td>"+oDrr[2]+"</td><td>"+oDrr[3]+"</td><td>"+oDrr[4]+"</td><td>1000</td></tr>";
oTB+="<td>给定比例</td><td>0.1</td><td>0.4</td><td>0.3</td><td>0.15</td><td>0.05</td><td>1</td></tr>";
oTB+="<td>样本比例</td><td>"+oDrr[0]/1000+"</td><td>"+oDrr[1]/1000+"</td><td>"+oDrr[2]/1000+"</td><td>"+oDrr[3]/1000+"</td><td>"+oDrr[4]/1000+"</td><td>1</td></tr>";
oTB+="</table>";
webTJ.display(oTB,0);

随着网络技术的迅猛发展和计算机数据处理能力的不断提升，大规模统计数据模拟和处理已比较容易实现。概率论与数理统计、组合数学、计算机算法和专业经验的有机结合，使得“世间万物皆可模拟”。统计数据模拟技术和数据挖掘技术相辅相成、相互认证。例如聚类和分类问题可以用统计数据模拟技术按给定模式逼真地模拟出待聚类或分类问题大样本，再用数据挖掘技术挖掘出给定模式，并进行对比检验。统计数据模拟技术可以通过生成大样本模拟仿真自然和社会现象，在大数据时代，统计数据模拟技术和数据挖掘技术具有广泛的综合运用应用前景。

代码窗口

注：可将例题实例代码复制、粘贴到“代码窗口”，点击“运行代码”获得计算结果（鼠标选择实例代码\(\rightarrow\)Ctrl+C:复制\(\rightarrow\)鼠标点击“代码窗口”使其获得焦点\(\rightarrow\)Ctrl+V:粘贴）

运行效果

posted @ 2017-02-23 09:09  银河统计  阅读(2721)  评论(0)  编辑  收藏  举报