常用分布随机数生成及JS类函数开发和运用

（2017-02-15 银河统计）

随机数生成是运用蒙特卡洛或统计随机模拟仿真方法的前提。本文在银河统计Web Service接口基础上，编制JS类函数生成常用分布随机数，为在网页中实现模拟仿真项目提供方便。相关参考文章统计随机数及临界值Web Service接口、在网页中运用统计Web Service接口和R语言-统计分布和模拟。

1、随机数生成及运用

随机数生成和赋值代码样例：

var oURL=webTJ1.wsFC.getURL("normal_r",100,4,0,1,0); //获得生成正态分布随机数接口网址（均值为0、标准差为1）
webTJ1.wsFC.setRSample(oURL,1); //将按指定oURL返回的随机数按数组格式赋值给系统变量webTJ1.wsRSArr1
webTJ1.wsFC.setRSample(oURL,10); //将按指定oURL返回的随机数按数组格式赋值给系统变量webTJ1.wsRSArrs[0]
var oURL1=webTJ1.wsFC.getURL("uniform_r",100,4,1,6,0); //获得生成均匀分布随机数接口网址
webTJ1.wsFC.setRSample(oURL1,2); //将按指定oURL返回的随机数按数组格式赋值给系统变量webTJ1.wsRSArr2
webTJ.display("生成随机数，并赋值给指定系统变量！",0);
注：根据设定的不同随机数接口变量oURL获取相应的随机数，并以数组格式赋值给指定系统变量，以备在“随机数运用代码”中调用。

随机数运用代码样例：

webTJ.clear();
webTJ.display(webTJ1.wsRSArr1,0);
webTJ.display(webTJ1.wsRSArrs[0],0);
webTJ.display(webTJ1.wsRSArr2,0);

随机数生成和赋值代码窗口

注：可将例题实例代码复制、粘贴到“代码窗口”，点击“运行代码”获得计算结果（鼠标选择实例代码\(\rightarrow\)Ctrl+C:复制\(\rightarrow\)鼠标点击“代码窗口”使其获得焦点\(\rightarrow\)Ctrl+V:粘贴）

随机数运用代码窗口

注：可将例题实例代码复制、粘贴到“代码窗口”，点击“运行代码”获得计算结果（鼠标选择实例代码\(\rightarrow\)Ctrl+C:复制\(\rightarrow\)鼠标点击“代码窗口”使其获得焦点\(\rightarrow\)Ctrl+V:粘贴）

代码运行效果

2、JS随机数生成类函数

（1）获得随机数接口网址

函数：webTJ1.wsFC.getURL(t,s,d,c1,c2,c3)
功能：根据参数返回统计Web Service接口网址
参数：参见getURL函数参数表（附表—1）

注：webTJ1父类名称、wsFC子类名称

附表-1：getURL函数参数表
序号t/分布类型s/样本数量d/保留小数c1/参数1c2/参数2c3/参数3备注
1normal_r1000401*正态分布
2uniform_r10004-11*均匀分布
3lnorm_r1000401*对数正态分布
4gamma_r100040.51*Gamma分布
5exp_r100041.5**指数分布
6chisq_r1000430*卡方分布
7beta_r100042.51.51β分布
8cauchy_r1000421*柯西分布
9t_r1000432*t分布
10f_r100042086F分布
11logis_r1000401*Logistic分布
12weibull_r1000421*韦伯分布
13pois_r100044**泊松分布
14binom_r100040.25**二项分布
15nbinom_r100040.25**负二项式分布
16geom_r100040.25**几何分布
17hyper_r100041078超几何分布
18wilcox_r1000446*Wilcoxon分布
19signrank_r1000410**秩和分布

注：函数getURL(t,s,d,c1,c2,c3)的参数和统计Web Service接口网址的对应关系为，t-type、s-sample_size、d-decimal_places、c1、c2、c3为各种分布的特有参数，c2、c3为*时分布无该参数。各分布特有参数取值参见统计随机数及临界值Web Service接口

（2）按指定接口返回随机数数组并赋值给系统变量

函数：webTJ1.wsFC.setRSample(url,id)
功能：根据指定接口返回回随机数数组并赋值给系统变量
参数：url为统计Web Service接口网址；
     id=1,2,...,9，返回随机数数组存储在系统变量webTJ1.wsRSArr1,webTJ1.wsRSArr2,...,webTJ1.wsRSArr9中；
     id>9，返回随机数数组存储在系统变量webTJ1.wsRSArr[id-10]中

注：id=1，返回随机数数组存储在系统变量webTJ1.wsRSArr1中；id=2，随机数数组存储在webTJ2.wsRSArr1中；id=10，返回随机数数组存储在系统变量webTJ1.wsRSArr[0]中；id=11，随机数数组存储在webTJ1.wsRSArr[1]中。这样即可在“随机数运用代码”框中灵活调用所生成的随机数组

3、统计随机模拟运用案例

统计随机模拟方法又称统计随机抽样或统计试验方法，更响亮的名字是蒙特卡洛模拟。当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是统计随机模拟方法的基本思想。这种方法是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

统计随机模拟方法解题归结为三个主要步骤：

构造或描述概率过程；
实现从已知概率分布抽样；
建立各种估计量。

（1）掷筛子随机试验及统计

模拟掷筛子N次，统计1-6点朝上的次数和频率。

I、问题分析：

掷筛子时，1-6点朝上的次数和概率（频率）相等，理论值为1/6。掷筛子N次随机试验的随机概率分布模型为均匀分布，例如掷筛子6000次可用生成6000个整数1-6的均匀分布样本来进行模拟。

II、生成均匀分布随机样本（JS代码片段1）

var oURL=webTJ1.wsFC.getURL("uniform_r",60000,4,0,1.2,0);//生成60000个0-1.2均匀分布样本统计接口网址
webTJ1.wsFC.setRSample(oURL,1); //将样本按数组格式赋值给系统变量webTJ1.wsRSArr1
webTJ.display("生成随机数！",0);

III、运用随机样本统计1-6点朝上的次数和频率（JS代码片段2）

webTJ.clear();
var oSample=webTJ1.wsRSArr1;
webTJ.display("均匀分布样本:<br/>"+oSample,0);
var oCount=[0,0,0,0,0,0];
var oLen=oSample.length;
for (var i=0; i<oLen; i++) {
  if(oSample[i]<0.2) {oCount[0]++;}
  if(oSample[i]>=0.2 && oSample[i]<0.4) {oCount[1]++;}
  if(oSample[i]>=0.4 && oSample[i]<0.6) {oCount[2]++;}
  if(oSample[i]>=0.6 && oSample[i]<0.8) {oCount[3]++;}
  if(oSample[i]>=0.8 && oSample[i]<1.0) {oCount[4]++;}
  if(oSample[i]>=1.0) {oCount[5]++;}
  }
var oTB="<table>";
oTB+="<caption>掷筛子"+oLen+"次1-6点朝上次数和概率表</caption>";
oTB+="<tr><td>点数</td><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td><td>6</td><td>合计</td></tr>";
oTB+="<tr><td>次数</td><td>"+oCount[0]+"</td><td>"+oCount[1]+"</td><td>"+oCount[2]+"</td><td>"+oCount[3]+"</td><td>"+oCount[4]+"</td><td>"+oCount[5]+"</td><td>"+oLen+"</td></tr>";
oTB+="<tr><td>概率</td><td>"+Math.round(10000*oCount[0]/oLen)/10000+"</td><td>"+Math.round(10000*oCount[1]/oLen)/10000+"</td><td>"+Math.round(10000*oCount[2]/oLen)/10000+"</td><td>"+Math.round(10000*oCount[3]/oLen)/10000+"</td><td>"+Math.round(10000*oCount[4]/oLen)/10000+"</td><td>"+Math.round(10000*oCount[5]/oLen)/10000+"</td><td>1</td></tr>";
oTB+="</table>";
oTB+="<i>注：1-6点朝上理论次数"+oLen/6+"、理论概率1/6=1.666666667</i><br/>";
webTJ.display(oTB,0);

IV、随机试验和统计实现步骤

第一步：将JS代码片段1复制、粘贴到“随机数生成和赋值代码”框，点击“运行随机数生成代码”按钮生成指定随机数数组并存入系统变量以供调用；
第二步：将JS代码片段2复制、粘贴到“随机数运用代码”框，点击“运行随机数应用代码”按钮，试验和统计结果显示在“代码运行效果”窗口中；
第三步：可以在“随机数生成和赋值代码”框修改JS代码片段1函数getURL("uniform_r",60000,4,0,1.2,0)的参数（如试验次数60000改为500，均匀分布上、下限为0-1.2方便分为6份），然后顺序点击“运行随机数生成代码”按钮和“运行随机数应用代码”按钮，从而获得新试验和统计结果，实现重复试验。

（2）赶火车问题蒙特卡洛模拟

一列火车从A站经过B站开往C站, 某人每天赶往B站乘这趟火车去C站，但是由于火车出发时间和运行时间以及该人在赶往B火车站的时间都具有一定的随机性，该旅客已知：

a. 火车从A站到B站运行时间为均值30分钟、标准差为2分钟的正态随机变量。火车大约在下午1点离开A站。离开时刻的频率分布为，

出发时刻（$T_1$）下午1:00下午1:05下午1:10
概率0.70.20.1

b. 设\(T_2\)为火车从A站到B站运行时间随机变量（均值30分钟、标准差为2分钟）；

c. 该旅客到达B站时间的概率分布，

达到时间（$T_3$）下午1:28下午1:30下午1:32下午1:34
概率0.30.40.20.1

I、问题分析：

已知，

    \(T_1\)：火车从A站出发时刻；
    \(T_2\)：火车从A站到B站运行时间；
    \(T_3\)：旅客到达B站时间。

假设\(T_1\)、\(T_2\)、\(T_3\)为相互独立的随机变量。为了简化问题，将下午1时记为\(t=0\)，\(T_1\)和\(T_3\)的概率分布简化如下：

出发时刻（$T_1$）0510
概率0.70.20.1

达到时间（$T_3$）28303234
概率0.30.40.20.1

如果R为(0,1)均匀分布随机数，可通过以下条件方程模拟随机变量\(T_1\)和\(T_3\)，

\[T_1= \begin{equation*} \begin{cases} 0,\qquad \hspace{2mm}(0\ge r <0.7)\\ 5,\qquad \hspace{2mm}(0.7\ge r <0.9)\\ 10,\qquad (0.9\ge r \ge 0.7)\\ \end{cases} \end{equation*} \]

\[T_3= \begin{equation*} \begin{cases} 28,\qquad (0\ge r <0.3)\\ 30,\qquad (0.3\ge r <0.7)\\ 32,\qquad (0.7\ge r <0.9)\\ 34,\qquad (0.9\ge r \ge 1.0)\\ \end{cases} \end{equation*} \]

随机变量\(T_3\sim N(30,2^2)\)。

该旅客能赶上火车的充要条件是：\(T_3<T_1+T_2\)。

II、生成随机样本（JS代码片段3）

webTJ.clear();
var oURL=webTJ1.wsFC.getURL("normal_r",10000,2,30,2,0); 
webTJ1.wsFC.setRSample(oURL,1); 
webTJ.display("生成随机数！",0);

III、运用随机样本计算该旅客赶上火车的概率（JS代码片段4）

webTJ.clear();
var oNSample=webTJ1.wsRSArr1;
var oLen=oNSample.length;
var oSum=0;
var t1, t2, t3, Us1, Us2, oYN;
var oTB="<table style='color:#555555; font-size:10pt;'>";
oTB+="<caption>赶火车问题统计模拟计算表</caption>";
oTB+="<tr><th>No.</th><th>Us1</th><th>Us2</th><th>T1</th><th>T2</th><th>T3</th><th>T3&lt;T1+T2</th></tr>";
for (var i=0; i<oLen; i++) {
  Us1=Math.round(10000*Math.random())/10000; Us2=Math.round(10000*Math.random())/10000; t2=oNSample[i];
  if (Us1<0.7) {t1=0;}
  if (Us1>=0.7 && Us1<0.9) {t1=5;}
  if (Us1>=0.9 && Us1<=1) {t1=10;}
  if (Us2<0.3) {t3=28;}
  if (Us2>=0.3 && Us2<0.7) {t3=30;}
  if (Us2>=0.7 && Us2<0.9) {t3=32;}
  if (Us2>=0.9 && Us2<=1) {t3=34;}
  if (t3<t1+t2) {oYN=1; oSum++;} else {oYN=0;}
  oTB+="<tr><td>"+(i+1)+"</td><td>"+Us1+"</td><td>"+Us2+"</td><td>"+t1+"</td><td>"+t2+"</td><td>"+t3+"</td><td>"+oYN+"</td></tr>";
  }
oTB+="</table>";
oTB+="<p><i>注：T1火车从A站出发时刻、T2火车从A站到B站运行时间、T3旅客到达B站时间、Us1和Us2均匀分布样本（由JS的Math.random函数生成）</i></p>";
oTB+="<div style='color:#ff5555; font-weight:bold; font-size:16pt;'>赶上火车概率="+Math.round(10000*oSum/oLen)/10000+"</div>";
webTJ.display(oTB,0);

IV、随机试验和统计实现步骤

第一步：将JS代码片段3复制、粘贴到“随机数生成和赋值代码”框，点击“运行随机数生成代码”按钮生成指定随机数数组并存入系统变量以供调用；
第二步：将JS代码片段4复制、粘贴到“随机数运用代码”框，点击“运行随机数应用代码”按钮，试验和统计结果显示在“代码运行效果”窗口中；
第三步：在“随机数生成和赋值代码”框无论是否修改修改JS代码片段3，顺序点击“运行随机数生成代码”按钮和“运行随机数应用代码”按钮可实现实现重复试验。

【统计随机模拟思考题】

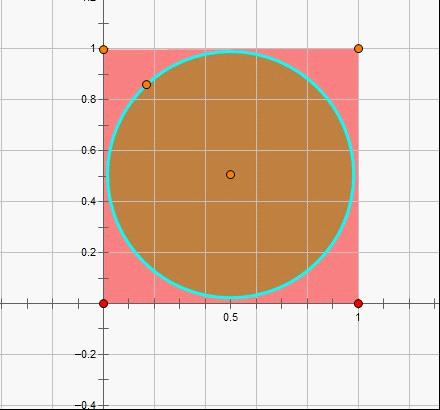
在图中运用随机投点法（蒙特卡洛算法）按掷筛子或赶火车实例步骤在网页中编程估计圆周率\(\pi\)。

运用JavaScript可以生成一些简单随机分布样本，但生成诸如F分布等很多模型有些力不从心。银河统计提供丰富的随机数生成Web Service接口，可以使得JS程序员可以在网页中轻松实现各种统计模拟试验。统计、数学爱好者稍有编程知识，即可在我们的博客园文章中完成您所设计的模拟项目。JS参考文章JavaScript脚本语言基础（一）。

posted @ 2017-02-15 11:11  银河统计  阅读(1338)  评论(0)  编辑  收藏  举报