统计随机数及临界值Web Service接口

（2017-02-04 银河统计）

统计函数API概念

  API（Application Programming Interface,应用程序编程接口）是一些预先定义的函数，目的是提供应用程序与开发人员基于某软件或硬件得以访问一组例程的能力，而又无需访问源码，或理解内部工作机制的细节。

  统计函数API是通过前台web网页传入数据和参数，服务器接收数据和参数后，经过统计计算返回结果的一种新型接口形式。

  通常前台web网页很难处理复杂数学或统计问题，通过Web Service技术将数据和参数递交给服务器，经过R、Python、.Net、PHP等处理后，按JSON格式返回计算结果，然后在网页中动态引用API函数接口，从而大大拓宽网页的统计数据处理能力。

蒙特卡罗方法

  蒙特卡罗（Monte Carlo）方法，又称随机抽样或统计试验方法，属于计算数学的一个分支，它是在上世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。

  当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

  蒙特卡罗解题可归结为三个主要步骤：

    构造或描述概率过程；
    实现从已知概率分布抽样（概率分布随机数模拟生成）；
    建立各种估计量。
#### **目录**

连续型随机样本及临界值

1.正态分布[返回]

（1）概述

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution）。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为\(σ^2\)的正态分布，记为N（μ，\(σ^2\)）。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0，σ=1时的正态分布是标准正态分布。

（2）密度函数及分布图形

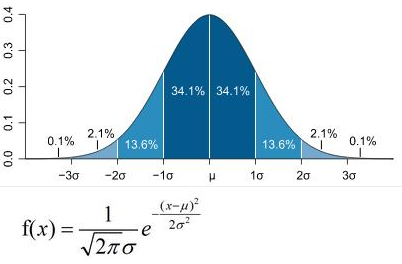
（3）性质

期望值：\(E(x)=\mu\)

标准差：\(D(x)=\sigma\)

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=normal_r&var_name=random_number&sample_size=100&decimal_places=4&mean_value=0&sd_value=1
	
	参数：
	【sample_size, mean_value, sd_value, decimal_places】
	【生成随机数数量, 均值, 标准差, 保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=normal_q&var_name=quantile_number&mean_value=0&sd_value=1&probit_value=0.975

	参数：
	【probit_value, mean_value, sd_value】
	【概率值（置信水平：1-α）, 均值, 标准差】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=normal_p&var_name=probit_number&mean_value=0&sd_value=1&quantile_value=0

	参数：
	【quantile_value, mean_value, sd_value】
	【分位数值, 均值, 标准差】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=normal_d&var_name=probit_density_num&mean_value=0&sd_value=1&decimal_places=4&random_num_arr=-1.4298|-1.3189|-1.2303|-0.2276|-0.0335|0.3198|0.3674|0.5244|0.5675|0.8554|-1.4298

	参数：
	【random_num_arr, mean_value, sd_value, decimal_places】
	【概率密度函数自变量数组, 均值, 标准差, 保留的小数位数】

2.均匀分布[返回]

（1）概述

均匀分布（Uniform Distribution）、均匀分布或称规则分布，是概率统计中的重要分布之一。均匀分布在自然情况下极为罕见，而人工栽培的有一定株行距的植物群落即是均匀分布。这表明X落在[a,b]的子区间内的概率只与子区间长度有关，而与子区间位置无关,因此X落在[a,b]的长度相等的子区间内的可能性是相等的，所谓的均匀指的就是这种等可能性。在实际问题中，当我们无法区分在区间[a,b]内取值的随机变量X取不同值的可能性有何不同时，我们就可以假定X服从[a,b]上的均匀分布。

（2）密度函数和分布函数

I、密度函数

\[f(x)=\frac{1}{b-a}\qquad(a\le x \le b) \]

II、分布函数

\[F(x)=\frac{x-a}{b-a}\qquad(a\le x \le b) \]

（3）性质

期望值：$$E(x)=\frac{a+b}{2}$$

标准差：$$D(x)=\frac{(b-a)^2}{12}$$

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=uniform_r&var_name=random_number&sample_size=100&decimal_places=4&lower_value=-1&upper_value=1
	
	参数：
	【sample_size, lower_value, upper_value, decimal_places】
	【生成随机数数量, 下限, 上限, 保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=uniform_q&var_name=quantile_number&lower_value=-1&upper_value=1&probit_value=0.5
	
	参数：
	【probit_value, lower_value, upper_value】
	【概率值, 下限, 上限】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=uniform_p&var_name=probit_number&lower_value=-1&upper_value=1&quantile_value=0

	参数：
	【quantile_value, lower_value, upper_value】
	【分位数值, 下限, 上限】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=uniform_d&var_name=probit_density_num&lower_value=-1&upper_value=1&decimal_places=4&random_num_arr=-0.4175|-0.3723|-0.2455|-0.1119|7e-04|0.5662|0.5663|0.6024|0.7033|0.7594

	参数：
	【random_num_arr, lower_value, upper_value, decimal_places】
	【概率密度函数自变量数组, 下限, 上限, 保留的小数位数】

3.对数正态分布[返回]

（1）概述

对数正态分布（logarithmic normal distribution），一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布。如果 X 是服从正态分布的随机变量，则 \(exp(X)\) 服从对数正态分布；同样，如果Y服从对数正态分布，则\(ln(Y)\)服从正态分布。 如果一个变量可以看作是许多很小独立因子的乘积，则这个变量可以看作是对数正态分布。一个典型的例子是股票投资的长期收益率，它可以看作是每天收益率的乘积。

（2）密度函数及分布图形

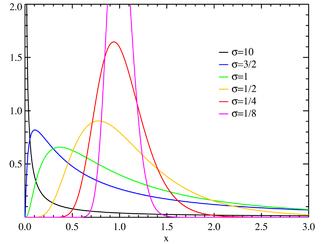
\[f(x)=\frac{1}{x\sigma\sqrt{2\pi}}e^{-\frac{(\ln{x}-\mu)^2}{2\sigma^2}} \]

（3）性质

期望值：$$E(x)=e{\mu+\frac{\sigma2}{2}}$$

标准差：$$D(x)=(e{\sigma2}-1)e{2\mu+\sigma2}$$

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=lnorm_r&var_name=random_number&sample_size=100&decimal_places=4&mean_value=0&sd_value=1

	参数：
	【sample_size, mean_value, sd_value, decimal_places】
	【生成随机数数量, 均值, 标准差, 保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=lnorm_q&var_name=quantile_number&mean_value=0&sd_value=1&probit_value=0.5

	参数：
	【probit_value, mean_value, sd_value】
	【概率值（置信水平：1-α）, 均值, 标准差】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=lnorm_p&var_name=probit_number&mean_value=0&sd_value=1&quantile_value=0

	参数：
	【quantile_value, mean_value, sd_value】
	【分位数值, 均值, 标准差】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=lnorm_d&var_name=probit_density_num&mean_value=0&sd_value=1&decimal_places=4&random_num_arr=0.0587|0.8444|1.1109|1.1152|1.1757|1.1911|1.4933|1.5742|2.5244|7.5273

	参数：
	【random_num_arr, mean_value, sd_value, decimal_places】
	【概率密度函数自变量数组, 均值, 标准差, 保留的小数位数】

4.Gamma(γ)分布[返回]

（1）概述

伽玛分布是统计学的一种连续概率函数。Gamma分布中的参数α，形状参数（shape parameter），β称为尺度参数（scale parameter）。在地震序列的有序性、地震发生率的齐次性、计数特征具有独立增量和平稳增量情况下，可以导出地震发生i次时间的概率密度为Gamma密度函数（亦称为Gamma分布）

（2）密度函数及分布图形

\[f(x)=\frac{(\alpha{x})^{\beta-1}}{\Gamma(\beta)}\alpha{e}^{-\alpha{x}}\qquad(0\le x<\infty) \]

其中，

\[\Gamma(\beta)=\int_0^{\infty}t^{\beta-1}e^{t}dt \]

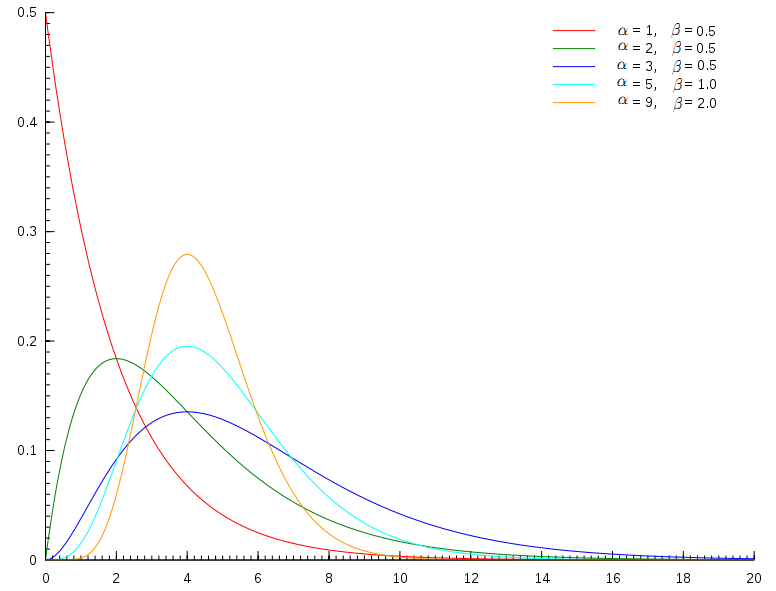
（3）性质

I、\(\beta=n\)，\(\Gamma(n,\alpha)\)就是Erlang分布。Erlang分布常用于可靠性理论和排队论中 ,如一个复杂系统中从第1次故障到恰好再出现n次故障所需的时间;从某一艘船到达港口直到恰好有n只船到达所需的时间都服从Erlang分布；

II、当\(\beta=1\)时，\(\Gamma(1,\alpha)\)就是参数为\(\alpha\)的指数分布,记为\(exp(\alpha)\) ；

III、当\(\alpha=\frac{n}{2}\)，\(\beta=\frac{1}{2}\)时，\(\Gamma(\frac{n}{2},\frac{1}{2})\)就是数理统计中常用的\(\chi^2(n)\) 分布；

IV、数学期望(均值)、方差

\[E(x)=\frac{\beta}{\alpha} \]

\[D(x)=\frac{\beta}{\alpha^2} \]

V、(Gamma 分布的可加性)：设随机变量 \(X_1,X_2,\dots,X_n\)相互独立，并且都服从Gamma分布，即\(X_i～\Gamma(\beta_i,\alpha)\)Xi，i =1,2,…,n, 则，

\[X_1,X_2,\dots,X_n～\Gamma(\beta_1+\beta_2+\dots+\beta_n,\alpha) \]

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=gamma_r&var_name=random_number&sample_size=100&decimal_places=4&shape_value=0.5&rate_value=1

	参数：
	【sample_size, shape_value, rate_value, decimal_places】
	【生成随机数数量, 形状参数α（shape parameter）, 尺度参数β（scale parameter）, 保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=gamma_q&var_name=quantile_number&shape_value=0.5&rate_value=1&probit_value=0.5

	参数：
	【probit_value, shape_value, rate_value】
	【概率值（置信水平：1-α）, 形状参数α, 尺度参数β】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=gamma_p&var_name=probit_number&shape_value=0.5&rate_value=1&quantile_value=0

	参数：
	【quantile_value, shape_value, rate_value】
	【分位数值, 形状参数α, 尺度参数β】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=gamma_d&var_name=probit_density_num&shape_value=0.5&rate_value=1&decimal_places=4&random_num_arr=0.0073|0.0117|0.0562|0.1912|0.2421|0.3004|0.4403|0.8675|1.1443|2.0391

	参数：
	【random_num_arr, shape_value, rate_value, decimal_places】
	【概率密度函数自变量数组, 形状参数α, 尺度参数β, 保留的小数位数】

5.指数分布[返回]

（1）概述

指数分布（Exponential distribution）可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。

指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，当s,t≥0时有P(T>s+t|T>t)=P(T>s)。即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少s+t小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。

（2）密度函数及分布图形

I、密度函数

\[f(x)=\lambda{e}^{-\lambda{x}}\qquad{x>0} \]

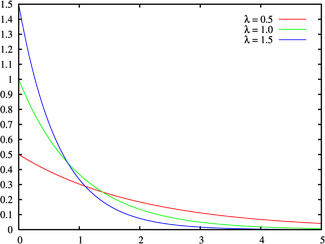
II、分布函数

\[F(x)=1-e^{-\lambda{x}}\qquad{x\ge{0}} \]

（3）性质

\[E(x)=\frac{1}{\lambda} \]

\[D(x)=\frac{1}{\lambda^2} \]

\[Q_L=\frac{ln(\frac{4}{3})}{\lambda} \]

\[Q_U=\frac{ln(2)}{\lambda} \]

\[M_e=\frac{ln(4)}{\lambda} \]

注：\(Q_L\)：下四分位数；\(Q_U\)：上四分位数；\(M_e\)：中分位数

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=exp_r&var_name=random_number&sample_size=100&decimal_places=4&rate_value=1.5

	参数：
	【sample_size, rate_value, decimal_places】
	【生成随机数数量，率参数λ, 保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=exp_q&var_name=quantile_number&rate_value=1.5&probit_value=0.5

	参数：
	【probit_value, rate_value】
	【概率值，率参数λ】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=exp_p&var_name=probit_number&rate_value=1.5&quantile_value=0

	参数：
	【quantile_value, rate_value】
	【分位数值，率参数λ】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=exp_d&var_name=probit_density_num&rate_value=1.5&decimal_places=4&random_num_arr=0.0162|0.075|0.2267|0.2757|0.4783|0.5716|0.8943|1.2323|1.4797|1.7181

	参数：
	【random_num_arr, rate_value, decimal_places】
	【概率密度函数自变量数组，率参数λ，保留的小数位数】

注：率参数\(\lambda\)即每单位时间内发生某事件的次数，例如，如果你平均每个小时接到2次电话，那么你预期等待每一次电话的时间是半个小时（\(E(x)=\frac{1}{\lambda}\)）

6.卡方分布[返回]

（1）概述

卡方分布是\(n\)个独立随机变量的平方和的分布规律，特点是当\(n\)增加时，分布曲线趋向于左右对称的正态分布。换言之，若\(n\)个相互独立的随机变量\(\xi_1,\xi_2,\dots,\xi_n\)，均服从标准正态分布（也称独立同分布于标准正态分布），则这\(n\)个服从标准正态分布的随机变量的平方和\(Q=\sum\limits_{i=1}^n\xi_i^2\)构成一新的随机变量，其分布规律称为\(\chi^2\)分布（chi-square distribution），其中参数\(n\)称为自由度。记为\(Q\sim\chi^2(n)\)。卡方分布是由正态分布构造而成的一个新的分布，当自由度\(n\)很大时，\(\chi^2\)分布近似为正态分布。卡方分布可以用来测试随机变量之间是否相互独立，也可用来检测统计模型是否符合实际要求。

（2）密度函数及分布图形

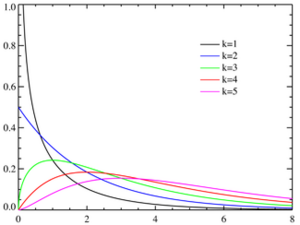
\[f(x,n)=\frac{x^{(\frac{n}{2}-1)}e^{-\frac{x}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}\qquad\qquad x\ge 0 \]

（3）性质

\[E(\chi^2)=n \]

\[D(\chi^2)=2n \]

注：\(n\)为自由度，\(\chi^2\)分布的均值为自由度\(n\)，分布的方差为2倍的自由度\(2n\)

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=chisq_r&var_name=random_number&sample_size=100&decimal_places=4&df_value=3&ncp_value=0

	参数：
	【sample_size, df_value, ncp_value, decimal_places】
	【生成随机数数量，自由度，非中心化参数，保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=chisq_q&var_name=quantile_number&df_value=3&ncp_value=0&probit_value=0.5

	参数：
	【probit_value, df_value, ncp_value】
	【概率值，自由度，非中心化参数】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=chisq_p&var_name=probit_number&df_value=3&ncp_value=0&quantile_value=0

	参数：
	【quantile_value, df_value, ncp_value】
	【分位数值，自由度，非中心化参数】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=chisq_d&var_name=probit_density_num&df_value=3&ncp_value=0&decimal_places=4&random_num_arr=0.0881|0.4838|0.8485|0.906|1.2199|1.8604|2.509|3.5463|6.0606|7.5377

	参数：
	【random_num_arr, df_value, ncp_value, decimal_places】
	【概率密度函数自变量数组，自由度，非中心化参数，保留的小数位数】

注：ncp_value为非中心化参数(non-centrality parameter)，卡方分布指正态分布的均值的平方和。\(ncp_value=0\)时是中心(central)卡方分布，\(ncp_value\neq 0\)时，表示这个卡方分布是由非标准正态分布组合而成

卡方分布、t分布、F分布等这一类以标准正态分布为基准的分布类的又衍生出了非中心化分布。他们都是基于期望不为0的正态分布为基准的分部类。这些分布的核心就是非中心化参数：

\[\lambda=\sqrt{\sum\limits_{i=1}^k(\frac{\mu_i}{\sigma_i})^2} \]

式中，\(\mu_i\)、\(\sigma_i\)为基准正态分布随机变量\(X_i\)的均值和标准差。

7.β分布[返回]

（1）概述

β分布（Beta Distribution)是一个作为伯努利分布和二项式分布共轭先验分布的密度函数，在机器学习和数理统计学中有重要应用。β分布可以看作一个概率的概率分布，当你不知道一个事件的具体概率是多少时，它可以给出了所有概率出现的可能性大小。在概率论和统计学中，二项分布是\(n\)个独立的（是/非）试验中成功的次数的离散概率分布，其中每次试验的成功概率为\(p\)。例如，

抛一次硬币出现正面的概率是0.6(p)，抛10(n)次硬币，出现k次正面的概率

在上面的例子中，每次抛硬币或者掷骰子都和上次的结果无关，所以每次实验都是独立的。二项分布是一个离散分布，k的取值范围为从0到n，只有n+1种可能的结果。

对于硬币或者骰子这样的简单实验，我们事先能很准确地掌握每次试验的成功概率。然而通常情况下，系统成功的概率是未知的。为了测试系统的成功概率p，我们做n次试验，统计成功的次数k，于是很直观地就可以计算出p=k/n。然而由于系统成功的概率是未知的，这个公式计算出的p只是系统成功概率的最佳估计。也就是说实际上p也可能为其它的值，只是为其它的值的概率较小。

例如有某种特殊的硬币，我们事先完全无法确定它出现正面的概率。然后抛10次硬币，出现5次正面，于是我们认为硬币出现正面的概率最可能是0.5。但是即使硬币出现正面的概率为0.4，也会出现抛10次出现5次正面的情况。因此我们并不能完全确定硬币出现正面的概率就是0.5，所以p也是一个随机变量，它符合β分布。

β分布是一个连续分布，由于它描述概率p的分布，因此变量x仅能出现于0到1之间，即其取值范围为0到1。 β分布有α和β两个参数，其中α为成功次数加1，β为失败次数加1。

（2）密度函数及分布图形

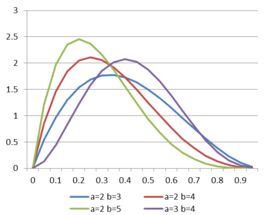
\[\begin{eqnarray*} f(x;\alpha,\beta)&=&\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0 ^1\mu^{\alpha-1}(1-\mu)^{\beta-1}d\mu}\\ &=&\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\\ &=&\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\\ \end{eqnarray*} \]

（3）性质

期望值：

\[E(x)=\frac{\alpha}{\alpha+\beta} \]

标准差：

\[D(x)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \]

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=beta_r&var_name=random_number&sample_size=100&decimal_places=4&shape1_value=2.5&shape2_value=1.5&ncp_value=1

	参数：
	【sample_size, shape1_value, shape2_value, ncp_value, decimal_places】
	【生成随机数数量，形状参数α，形状参数β，非中心化参数，保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=beta_q&var_name=quantile_number&shape1_value=2.5&shape2_value=1.5&ncp_value=1&probit_value=0.5

	参数：
	【probit_value, shape1_value, shape2_value, ncp_value】
	【概率值，形状参数α，形状参数β，非中心化参数】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=beta_p&var_name=probit_number&shape1_value=2.5&shape2_value=1.5&ncp_value=1&quantile_value=0

	参数：
	【quantile_value, shape1_value, shape2_value, ncp_value】
	【分位数值，形状参数α，形状参数β，非中心化参数】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=beta_d&var_name=probit_density_num&shape1_value=2.5&shape2_value=1.5&ncp_value=1&decimal_places=4&random_num_arr=0.2027|0.31|0.4615|0.5291|0.6932|0.7159|0.8336|0.8836|0.9372|0.9947

	参数：
	【random_num_arr, shape1_value, shape2_value, ncp_value, decimal_places】
	【概率密度函数自变量数组，形状参数α，形状参数β，非中心化参数，保留的小数位数】

8.柯西分布[返回]

（1）概述

柯西分布(Cauchy distribution)也叫柯西-洛伦兹分布，它是以奥古斯丁·路易·柯西与亨德里克·洛伦兹名字命名的连续概率分布。

柯西分布和正态分布是极易混淆的分布曲线。洛仑兹线性分布更适合于那种比较扁、宽的曲线。高斯线性分布则适合较高、较窄的曲线。如果是比较居中的情况，两者都可以。很多情况下，采用的是两者各占一定比例的做法。如洛伦茨占60%，高斯占40%.

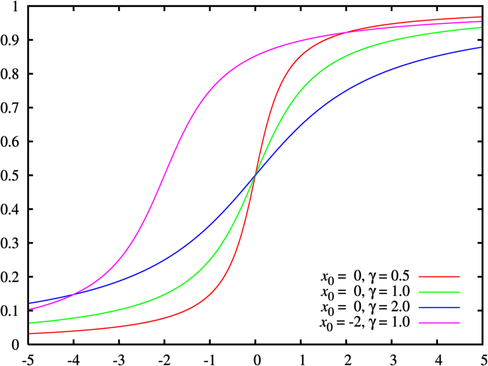
（2）密度函数、分布函数及分布图形

密度函数：

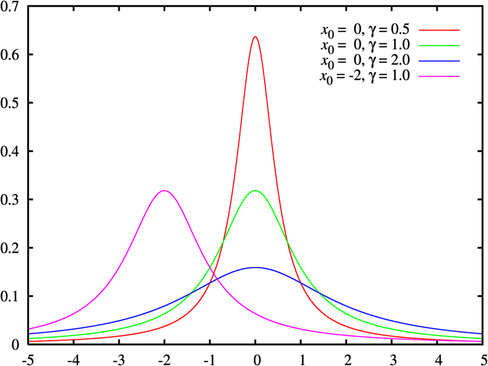
\[f(x;x_{_o},\gamma)=\frac{1}{\pi\gamma[1+(\frac{x-x_{_o}}{\gamma})^2]}=\frac{1}{\pi}[\frac{\gamma}{(x-x_{_o})^2+\gamma^2}] \]

分布函数：

\[F(x;x_{_o},\gamma)=\frac{1}{\pi}arctan(\frac{x-x_{_o}}{\gamma})+1 \]

（3）性质

无均值和标准差，\(中位数=众数=x-x_{_o}\)。

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=cauchy_r&var_name=random_number&sample_size=100&decimal_places=4&location_value=2&scale_value=1

	参数：
	【sample_size, location_value, scale_value, decimal_places】
	【生成随机数数量，位置参数，尺度参数，保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=cauchy_q&var_name=quantile_number&location_value=2&scale_value=1&probit_value=0.5

	参数：
	【probit_value, location_value, scale_value】
	【概率值，位置参数，尺度参数】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=cauchy_p&var_name=probit_number&location_value=2&scale_value=1&quantile_value=0

	参数：
	【quantile_value, location_value, scale_value】
	【分位数值，位置参数，尺度参数】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=cauchy_d&var_name=probit_density_num&location_value=2&scale_value=1&decimal_places=4&random_num_arr=-9.2498|0.65|1.6594|2.5913|2.8088|2.8542|3.9438|4.6416|4.8556|8.1641

	参数：
	【random_num_arr, location_value, scale_value, decimal_places】
	【概率密度函数自变量数组，位置参数，尺度参数，保留的小数位数】

注：其中location_value(\(x_{_o}\))是定义分布峰值位置的位置参数，scale_value(\(\gamma\))是最大值一半处的一半宽度的尺度参数

9.t分布[返回]

（1）概述

设\(\xi\)服从标准正态分布\(N(0,1)\)，\(\eta\)服从自由度为\(n\)的\(\chi^2(n)\)分布，且\(\xi、\eta\)相互独立，则称变量\(\tau=\frac{\xi}{\sqrt{(\frac{\eta}{n})}}\)所服从的分布为自由度为n的\(t\)分布(Student's t-distribution)。

在概率论和统计学中，\(t\)分布经常应用在对呈正态分布的总体的均值进行估计。它是对两个样本均值差异进行显着性测试的基础。t检验改进了正态检验，不论样本数量大或小皆可应用。在样本数量大（超过120等）时，可以应用正态检验，但正态检验用在小的样本会产生很大的误差。因此样本很小的情况下得改用学生t检验。

以0为中心，左右对称的单峰分布。t分布是一簇曲线，其形态变化自由度n大小有关。自由度n越小，t分布曲线越低平；自由度n越大，t分布曲线越接近标准正态分布曲线。

（2）密度函数及分布图形

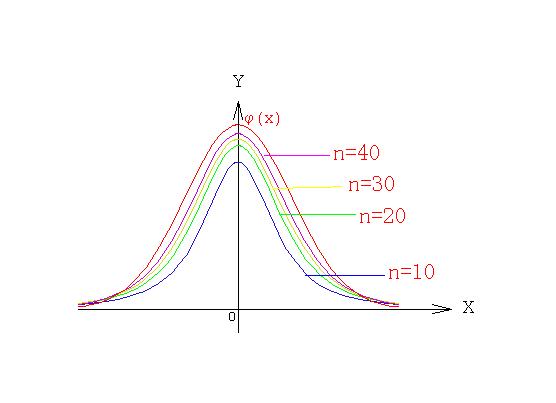
\[f(x;n)=\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})\sqrt{n\pi}}(1+\frac{x^2}{n})^{-\frac{n+1}{2}} \]

（3）性质

期望值：

\[E(x)=0\qquad n>1 \]

标准差：

\[D(x)=\frac{n}{n-2}\qquad n>2 \]

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=t_r&var_name=random_number&sample_size=100&decimal_places=4&df_value=3&ncp_value=2

	参数：
	【sample_size, df_value, ncp_value, decimal_places】
	【生成随机数数量，自由度n，非中心化参数，保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=t_q&var_name=quantile_number&df_value=3&ncp_value=2&probit_value=0.5

	参数：
	【probit_value, df_value, ncp_value】
	【概率值，自由度n，非中心化参数】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=t_p&var_name=probit_number&df_value=3&ncp_value=2&quantile_value=0

	参数：
	【quantile_value, df_value, ncp_value】
	【分位数值，自由度n，非中心化参数】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=t_d&var_name=probit_density_num&df_value=3&ncp_value=2&decimal_places=4&random_num_arr=0.4654|0.5159|0.8742|1.5858|1.6824|1.8721|2.1079|2.5161|4.3163|4.5852

	参数：
	【random_num_arr, df_value, ncp_value, decimal_places】
	【概率密度函数自变量数组，自由度n，非中心化参数，保留的小数位数】

10.F分布[返回]

（1）概述

随机变量\(\xi\)、\(\eta\)服从自由度为\(n_1\)、\(n_2\)的\(\chi^2\)分布，且\(\xi\)与\(\eta\)相互独立，则\(\tau=\frac{\frac{\xi}{n_1}}{\frac{\eta}{n_2}}\)服从自由度为\(n_1\)、\(n_2\)的\(F\)分布。

F分布是1924年英国统计学家R.A.Fisher提出，并以其姓氏的第一个字母命名的，在统计学中用于方差分析、协方差分析和回归分析等。

F分布是一种非对称分布，它有两个自由度\(n_1\)、\(n_2\)，\(n_1\)通常称为分子自由度（第一自由度），\(n_2\)通常称为分母自由度（第二自由度）。F分布是一个以自由度\(n_1\)和\(n_2\)为参数的分布族，不同的自由度决定了\(F\)分布的形状。

（2）密度函数及分布图形

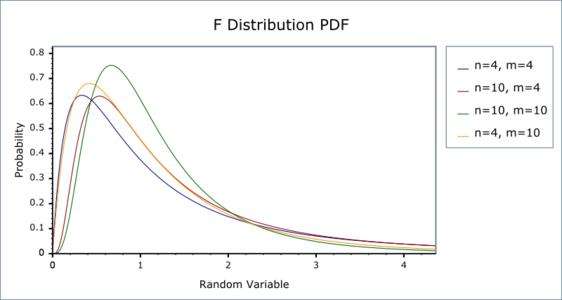
\[f(x;n_1,n_2)=\frac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2})\Gamma(\frac{n_2}{2})}(\frac{n_1}{n_2})^{\frac{n_1}{2}}x^{\frac{n_1}{2}-1}(1+\frac{n_1}{n_2}x)^{-\frac{n_1+n_2}{2}}\qquad x>0 \]

（3）性质

期望值：

\[E(x)=\frac{n_2}{n_2-2}\qquad n_2>2 \]

标准差：

\[D(x)=\frac{2{n_2}^2(n_1+n_2-2)}{n_1(n_2-2)(n_2-4)}\qquad n_2>4 \]

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=f_r&var_name=random_number&sample_size=100&decimal_places=4&df1_value=20&df2_value=8&ncp_value=6

	参数：
	【sample_size, df1_value, df2_value, ncp_value, decimal_places】
	【生成随机数数量，分子自由度n，分母自由度n，非中心化参数，保留的小数位数】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=f_q&var_name=quantile_number&df1_value=20&df2_value=8&ncp_value=6&probit_value=0.5

	参数：
	【probit_value, df1_value, df2_value, ncp_value】
	【概率值，分子自由度n，分母自由度n，非中心化参数】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=f_p&var_name=probit_number&df1_value=20&df2_value=8&ncp_value=6&quantile_value=0

	参数：
	【quantile_value, df1_value, df2_value, ncp_value】
	【分位数值，分子自由度n，分母自由度n，非中心化参数】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=f_d&var_name=probit_density_num&df1_value=20&df2_value=8&ncp_value=6&decimal_places=4&random_num_arr=0.775|0.8618|0.9225|1.0359|1.2735|1.4574|2.2061|2.6408|3.0825|5.3007

	参数：
	【random_num_arr, df1_value, df2_value, ncp_value, decimal_places】
	【概率密度函数自变量数组，分子自由度n，分母自由度n，非中心化参数，保留的小数位数】

11.Logistic分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=logis_r&var_name=random_number&sample_size=100&decimal_places=4&location_value=0&scale_value=1

	参数：
	【sample_size, location_value, scale_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=logis_q&var_name=quantile_number&location_value=0&scale_value=1&probit_value=0.5

	参数：
	【probit_value, location_value, scale_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=logis_p&var_name=probit_number&location_value=0&scale_value=1&quantile_value=0

	参数：
	【quantile_value, location_value, scale_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=logis_d&var_name=probit_density_num&location_value=0&scale_value=1&decimal_places=4&random_num_arr=-4.3442|-2.3035|-1.3665|-1.2363|-0.9032|0.4973|1.1368|1.2495|1.7321|6.057

	参数：
	【random_num_arr, location_value, scale_value, decimal_places】
	【】

12.韦伯分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=weibull_r&var_name=random_number&sample_size=100&decimal_places=4&shape_value=2&scale_value=1

	参数：
	【sample_size, shape_value, scale_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=weibull_q&var_name=quantile_number&shape_value=2&scale_value=1&probit_value=0.5

	参数：
	【probit_value, shape_value, scale_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=weibull_p&var_name=probit_number&shape_value=2&scale_value=1&quantile_value=0

	参数：
	【quantile_value, shape_value, scale_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=weibull_d&var_name=probit_density_num&shape_value=2&scale_value=1&decimal_places=4&random_num_arr=0.2186|0.4354|0.4376|0.4422|0.4874|0.5362|0.7553|0.8223|0.8794|0.9306

	参数：
	【random_num_arr, shape_value, scale_value, decimal_places】
	【】

离散型随机样本及临界值

1.泊松分布[返回]

（1）概述

Poisson分布（Poisson distribution），译名有泊松分布、普阿松分布等，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。泊松分布的期望和方差均为λ，参数λ是单位时间(或单位面积)内随机事件的平均发生率。泊松分布适合于描述单位时间内随机事件发生的次数。

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当\(n\ge 10, p\le 0.1\)时，就可以用泊松公式近似得计算。

在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位。

（2）密度函数及分布图形

\[P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!} \]

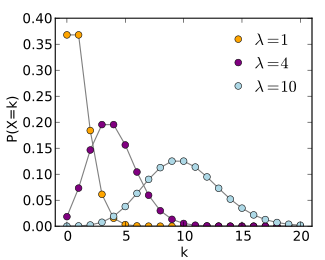
（3）性质

期望值：\(E(x)=\lambda\)

标准差：\(D(x)=\sqrt{\lambda}\)

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=pois_r&var_name=random_number&sample_size=100&decimal_places=0&labmda_value=4
	
	参数：
	【sample_size, labmda_value】
	【生成随机数数量, labmda值】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=pois_q&var_name=quantile_number&labmda_value=4&probit_value=0.5
	
	参数：
	【probit_value, labmda_value】
	【概率值, labmda值】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=pois_p&var_name=probit_number&labmda_value=4&quantile_value=0

	参数：
	【quantile_value, labmda_value】
	【分位数值, labmda值】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=pois_d&var_name=probit_density_num&labmda_value=4&decimal_places=4&random_num_arr=2|3|3|4|4|5|5|5|6|7

	参数：
	【random_num_arr, labmda_value, decimal_places】
	【概率密度函数自变量数组, labmda值, 保留的小数位数】

2.二项分布[返回]

（1）概述

二项分布（Binomial Distribution）即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

在概率论和统计学中，二项分布是n个独立的“是/非”试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次“成功/失败”试验又称为伯努利试验。实际上，当n = 1时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

二项分布在心理与教育研究中，主要用于解决含有机遇性质的问题。所谓机遇问题，即指在实验或调查中，实验结果可能是由 ?猜测而造成的。比如，选择题目的回答，划对划错，可能完全由猜测造成。凡此类问题，欲区分由猜测而造成的结果与真实的结果之间的界限，就要应用二项分布来解决。

（2）密度函数及分布图形

\[B(k,n,p)=C_{n}^{x}p^{x}(1-p)^{n-x} \]

其中，

\[C_{n}^{x}=\frac{n!}{x!(n-x)!} \]

式中x＝0、1、2、3．．．．．n为正整数。

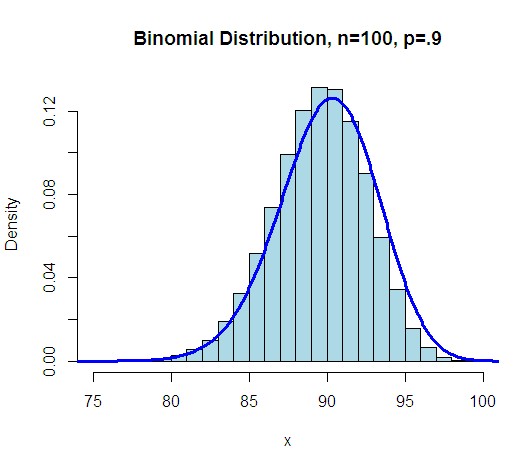
（3）性质

期望值：\(E(x)=np\)

标准差：\(D(x)=\sqrt{np(1-p)}\)

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=binom_r&var_name=random_number&sample_size=100&decimal_places=0&size_value=100&prob_value=0.25
	
	参数：
	【sample_size, size_value, prob_value】
	【生成随机数数量, 实验次数, 概率值】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=binom_q&var_name=quantile_number&size_value=100&prob_value=0.25&probit_value=0.5
	
	参数：
	【probit_value, size_value, prob_value】
	【概率值, 实验次数, 概率值】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=binom_p&var_name=probit_number&size_value=100&prob_value=0.25&quantile_value=25

	参数：
	【quantile_value, size_value, prob_value】
	【分位数值, 实验次数, 概率值】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=binom_d&var_name=probit_density_num&size_value=100&prob_value=0.25&decimal_places=4&random_num_arr=17|21|21|21|23|24|25|26|26|29

	参数：
	【random_num_arr, size_value, prob_value, decimal_places】
	【概率密度函数自变量数组, 实验次数, 概率值, 保留的小数位数】

3.负二项式分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=nbinom_r&var_name=random_number&sample_size=100&decimal_places=4&size_value=100&prob_value=0.25

	参数：
	【sample_size, size_value, prob_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=nbinom_q&var_name=quantile_number&size_value=100&prob_value=0.25&probit_value=0.5

	参数：
	【probit_value, size_value, prob_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=nbinom_p&var_name=probit_number&size_value=100&prob_value=0.25&quantile_value=25

	参数：
	【quantile_value, size_value, prob_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=nbinom_d&var_name=probit_density_num&size_value=100&prob_value=0.25&decimal_places=4&random_num_arr=226|247|271|271|282|283|283|308|311|338

	参数：
	【random_num_arr, size_value, prob_value, decimal_places】
	【】

4.几何分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=geom_r&var_name=random_number&sample_size=100&decimal_places=4&prob_value=0.25

	参数：
	【sample_size, prob_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=geom_q&var_name=quantile_number&prob_value=0.25&probit_value=0.5

	参数：
	【probit_value, prob_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=geom_p&var_name=probit_number&prob_value=0.25&quantile_value=25

	参数：
	【quantile_value, prob_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=geom_d&var_name=probit_density_num&prob_value=0.25&decimal_places=4&random_num_arr=0|0|0|0|1|1|1|2|4|5

	参数：
	【random_num_arr, prob_value, decimal_places】
	【】

5.超几何分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=hyper_r&var_name=random_number&sample_size=100&decimal_places=4&m_value=10&n_value=7&k_value=8

	参数：
	【sample_size, m_value, n_value, k_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=hyper_q&var_name=quantile_number&m_value=10&n_value=7&k_value=8&probit_value=0.5

	参数：
	【probit_value, m_value, n_value, k_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=hyper_p&var_name=probit_number&m_value=10&n_value=7&k_value=8&quantile_value=25

	参数：
	【quantile_value, m_value, n_value, k_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=hyper_d&var_name=probit_density_num&m_value=10&n_value=7&k_value=8&decimal_places=4&random_num_arr=4|4|5|6|6|6|6|6|6|6

	参数：
	【random_num_arr, m_value, n_value, k_value, decimal_places】
	【】

6.Wilcoxon分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=signrank_r&var_name=random_number&sample_size=100&decimal_places=4&n_value=10

	参数：
	【sample_size, n_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=signrank_q&var_name=quantile_number&n_value=10&probit_value=0.5

	参数：
	【probit_value, n_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=signrank_p&var_name=probit_number&n_value=10&quantile_value=25

	参数：
	【quantile_value, n_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=signrank_d&var_name=probit_density_num&n_value=10&decimal_places=4&random_num_arr=9|12|20|23|24|31|33|39|43|46

	参数：
	【random_num_arr, n_value, decimal_places】
	【】

7.秩和分布[返回]

（1）概述

（2）密度函数及分布图形

（3）性质

（4）Web Service接口及参数

### 随机数
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=wilcox_r&var_name=random_number&sample_size=100&decimal_places=4&m_value=4&n_value=6

	参数：
	【sample_size, m_value, n_value, decimal_places】
	【】

### 分位数（临界值）
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=wilcox_q&var_name=quantile_number&m_value=4&n_value=6&probit_value=0.5

	参数：
	【probit_value, m_value, n_value】
	【】

### 累计概率值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=wilcox_p&var_name=probit_number&m_value=4&n_value=6&quantile_value=25

	参数：
	【quantile_value, m_value, n_value】
	【】

### 概率密度值
	http://data.galaxystatistics.com:8881/?token=098f6bcd4621d373cade4e832627b4f6&type=wilcox_d&var_name=probit_density_num&m_value=4&n_value=6&decimal_places=4&random_num_arr=7|8|9|10|10|11|19|20|21|22

	参数：
	【random_num_arr, m_value, n_value, decimal_places】
	【】
posted @ 2017-02-05 01:55  银河统计  阅读(1210)  评论(0)  编辑  收藏  举报