总结一下几种优化方法

很多问题最终都归结为求一个算式的最小值问题，比如某个问题用MAP(最大后验概率)，ML(最大似然估计)等等方式来建立数学模型，最终就归结为在L1或L2范数下的最小值问题，这在很多文献中都经常碰到。而解决的方法，也不外乎几种：牛顿法、最速下降法、共轭梯度法、高斯牛顿法等等。名字都很相似，文献中也经常不描述具体的求解过程，往往让人一头雾水。今天我们就来梳理一下这些方法。

1、牛顿法

牛顿法最初是用来求解一个方程的根: f(x)=0

如上图所示，f(x)首先可以在x0点展开成一个线性函数f(x)≈f(x0)+f'(x0)*(x-x0)

求解上述线性方程的根，得到 x1=x0－f(x0)/f'(x0)，从图示可以看出这个x1比x0更加逼近原方程的根

用此方法，不断地迭代x(n+1)=xn-f(xn)/f'(xn)，就能无限趋近于原方程的根。

在最优化方法中，我们是想求一个算式f(x)的最优值，由微积分的知识我们知道，在f(x)的极值处，f'(x)=0

为此就可以用牛顿法来求解上述方程的根了，迭代过程为

上面推导的是一维的情况，比较直观，对于二维以上的情况，f'(x)演变成一个梯度向量▽f，f''(x)则演变成了一个矩阵，叫Hessian矩阵，估计大家不会陌生

此时牛顿法演变成

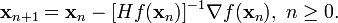
其中Hessian矩阵Hf(x)为

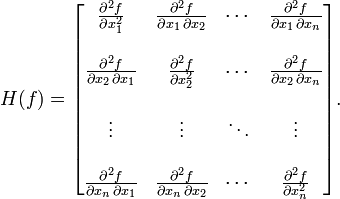
以上步长为1的迭代方法并不常见，常见的迭代方式是取一个小步长γ

$\mathbf{x}_{n+1} = \mathbf{x}_n - \gamma[H f(\mathbf{x}_n)]^{-1} \nabla f(\mathbf{x}_n).$

wiki上有张图，用来说明二维情况下牛顿法的效果。图中红线是牛顿法的迭代过程，绿线是梯度下降法的迭代过程。

一般认为牛顿方法因为用到了曲率信息(curvature，也就是二阶导数)，因此收敛速度比梯度下降法快得多。

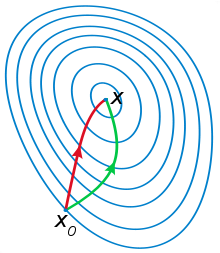
(图片来源: http://en.wikipedia.org/wiki/Newton%27s_method_in_optimization)

但在高维时，直接计算Hessian矩阵非常复杂，而且Hessian矩阵求逆也往往带来不稳定性，导致结果不收敛。为此有很多准牛顿法(quasi-Newton)，用近似的方法来构造Hessian矩阵。而为解决Hessian矩阵的不可逆性，也出现了很多算法，比如可以仿照Levenberg-Marquardt方法(著名的LM方法)，在Hessian矩阵上再加一个加权的单位矩阵 $\mu \mathbf I$ ,用来保证收敛过程的稳定性。权值μ是每步可调整的，当μ很大时，算法更加接近梯度下降法；当μ很小时，算法更加接近牛顿法。

2、高斯牛顿法(Gauss-Newton Method)

(参考:http://en.wikipedia.org/wiki/Gauss%E2%80%93Newton_algorithm)

首先要明确高斯牛顿法的适用场合：它只能用于非线性最小二乘问题(can only be used to minimize a sum of squared function values)

它是在牛顿方法的基础上改进过来的，它的优点是不需要求解二阶的Hessian矩阵

同样是采用迭代的方法，高斯牛顿法旨在寻求以下非线性最小二乘问题的最优解

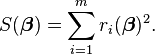
$S(\boldsymbol \beta)= \sum_{i=1}^m r_i(\boldsymbol \beta)^2.$

其中β是一个n维向量。m≥n以保证β取值维一。

高斯牛顿方法的迭代过程为

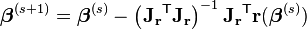
$\boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} - \left(\mathbf{J_r}^\mathsf{T} \mathbf{J_r} \right)^{-1} \mathbf{ J_r} ^\mathsf{T} \mathbf{r}(\boldsymbol \beta^{(s)})$

其中T代表矩阵转置。Jr表示Jacobian矩阵

$(\mathbf{J_r})_{ij} = \frac{\partial r_i (\boldsymbol \beta^{(s)})}{\partial \beta_j},$

进一步地，如果m=n，则迭代过程中的矩阵求逆可以展开，从而迭代过程简化为

$\boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} - \left( \mathbf{J_r} \right)^{-1} \mathbf{r}(\boldsymbol \beta^{(s)})$

对于数据拟合问题，问题表述为对模型y = f(x, β) ，求解参数β，使得实测点(xi,yi)带入上述模型拟合时残差最小，即

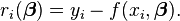
$r_i(\boldsymbol \beta)= y_i - f(x_i, \boldsymbol \beta).$

注意上式中f(x)前面有负号，所以求解参数β的迭代过程化为

$\boldsymbol \beta^{(s+1)} = \boldsymbol \beta^{(s)} + \left(\mathbf{J_f}^\mathsf{T} \mathbf{J_f} \right)^{-1} \mathbf{ J_f} ^\mathsf{T}\mathbf{r}(\boldsymbol \beta^{(s)}).$

同样地，高斯牛顿方法有时也会不稳定，不能保证收敛。这时无所不在的LM方法又出现了，假设迭代过程为

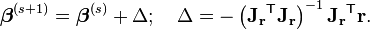
$\boldsymbol{\beta}^{(s+1)} = \boldsymbol\beta^{(s)}+\Delta;\quad \Delta = -\left( \mathbf{J_r}^\mathsf{T}\mathbf{J_r} \right)^{-1} \mathbf{J_r}^\mathsf{T}\mathbf{r}.$

J‘J求逆不是不稳定吗，那我在求解的时候对它进行一点修改，求解Δ相当于解下列方程

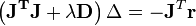
$\left(\mathbf{J^TJ+\lambda D}\right)\Delta=-\mathbf{J}^T \mathbf{r}$

其中D是一个正的对角阵。当D为单位矩阵，而λ又很大时，迭代过程基本就沿着梯度下降的方向进行了。通过调整λ和D(比如通过line search)，可以在收敛速度和稳定性之间找到一个平衡。

3、梯度下降法(Gradient descent)

梯度下降法大家是最熟悉的了，有时也叫最速下降法，迭代过程为

$\mathbf{x}_{n+1}=\mathbf{x}_n-\gamma_n \nabla F(\mathbf{x}_n),\ n \ge 0.$

就是说每次我都沿着最陡的方向向下走，那我每次都能下降最多，最终到达谷底(最小值点)也就越快

直观上，梯度下降应该下降最快才对啊，但其实不然，wiki上有几个例子，我只挑其中一个，其他的可以自己去看(http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95)

这个例子是求以下二维函数的最大值

$F(x,y)=\sin\left(\frac{1}{2} x^2 - \frac{1}{4} y^2 + 3 \right) \cos(2 x+1-e^y)$

把梯度下降的过程画在函数的等高线上，如下图。

可以看到梯度下降法每两次搜索过程之间是几乎垂直的，这里解释一下。

我们平时用梯度下降法，往往为追求简单，步长都取一个固定值，这样慢慢去逼近最小值。这样，步长的取值其实是有点带有经验性，如果步长取得太小，收敛就很慢。步长取得太大，又容易导致振荡，在极值点附近徘徊，不收敛。正确的做法是每次步长的选择都利用line search等方法沿着一个方向搜索，取这个方向的极值，然后确定的步长。而如果采用这种方法，对于某些函数，就会出现这种之字形的下降，导致收敛变得很慢。

由此我们可以看出梯度下降法的缺点：

1、下降过程可能会是之字形

2、直线搜索可能会出现问题

3、靠近极小值时收敛变慢

关于梯度下降和牛顿法的直观理解，可以参考知乎上的一观点

http://www.zhihu.com/question/19723347

为便于直观理解，在二维情况下来描述。牛顿法实际上相当于用二次曲面来拟合当前的局部曲面，而梯度下降法是用平面来拟合当前的局部曲面。而对于复杂的曲面，二次拟合往往比一次拟合要好。从另一个角度，梯度下降法只用到了一阶导数信息，相当于往当前坡度最大的方向走一步；而牛顿法不但用到了一阶导数，还用到了二阶导数信息，因此比梯度下降法看得更远，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大，因此能更快收敛。牛顿法的缺点是初值离目标太远时容易导致不收敛。

4、共轭梯度法

(参考了http://jacoxu.com/?p=242)

首先解释一个名词，共轭一般意味着正交。因此共轭梯度法我们从直观上简单理解，就是搜索方向互相正交的方法。

参考的这篇文章，写得非常直观易懂，我自知不可能写得更好了，由于原文里有很多公式没法拷过来，因此用图片将原文照搬过来

(以下图片截自http://jacoxu.com/?p=242，版权属于原作者)