[DeeplearningAI笔记]第二章3.1-3.2超参数搜索技巧
[DeeplearningAI笔记]第二章3.1-3.2超参数搜索技巧
觉得有用的话,欢迎一起讨论相互学习~
3.1 调试处理
需要调节的参数
- 级别一:\(\alpha\)学习率是最重要的需要调节的参数
- 级别二:
- Momentum参数 \(\beta\) 0.9是个很好的默认值
- mini-batch size,以确保最优算法运行有效
- 隐藏单元数量
- 级别三:
- 层数 , 层数有时会产生很大的影响.
- learning rate decay 学习率衰减
- 级别四:
- NG在使用Adam算法时几乎不会调整\(\beta_{1},\beta_{2},\epsilon 的大小\)一般会使用默认的选定值,即\(\beta_{1}=0.9 , \beta_{2}=0.999 , \epsilon=10^{-8}\)
如何选择参数
solution1随机取值
- 在早期的机器学习算法中,如果你有两个需要选择的超参数--超参一和超参二,常见的做法是在网格中取样点,然后系统的研究这些数值.
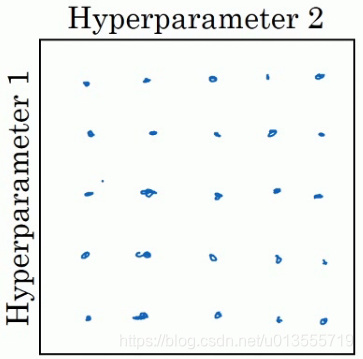
- 在参数较少的时候,此方法的确很实用,但是对于参数较多的深度学习领域,我们常做的是随机选择点.这个方法是因为对于你要解决的问题而言,你很难提前知道那个超参数最重要.
-
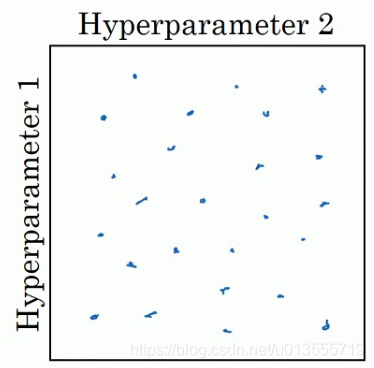
这个问题,我们可以这样来理解.
- 假设超参数一指的是学习率\(\alpha\),超参数二是Adam算法中的\(\epsilon\),在这种情况下,我们知道\(\alpha\)很重要,但是\(\epsilon\)的取值却无关紧要,如果你在网格中取点,接着你试验了\(\alpha\)的5个取值,那你会发现无论\(\epsilon\)如何取值,结果基本上都是一样的.所以即使你考虑了25个值,但进行实验的\(\alpha\)值只有5个
- 对比而言,如果你随机取值,你会试验25个独立的\(\alpha\)值,所以你似乎会更可能发现效果更好的取值.
-
对于高维参数
- 例如如果你有三个参数,你搜索的不是一个平面,而是一个立方体.超参数三代表第三维,接着在这个三维空间中取值,你会试验大量的更多的值.
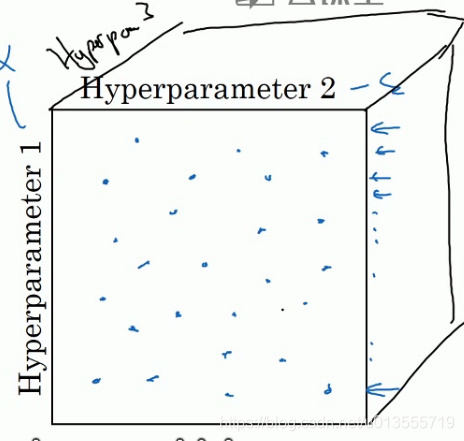
- 实际中,你会在一个更高维的空间中寻找超参数,随机取值,代表了你探究了更多超参数的潜在值.
solution2粗糙到精确取值
- 另一个惯例是采用有粗糙到精细的策略
- 比如你在二维的例子中,你进行了取值,也许你会发现效果更好的某个点,也许这个点周围的其他一些点效果也很好,那么接下来你需要放大这块小区域,然后在其中更密集的随机取值,聚集更多的资源,在这个红色的方格中进行搜索,然后逐渐缩小范围,直到到达一个满意的取值
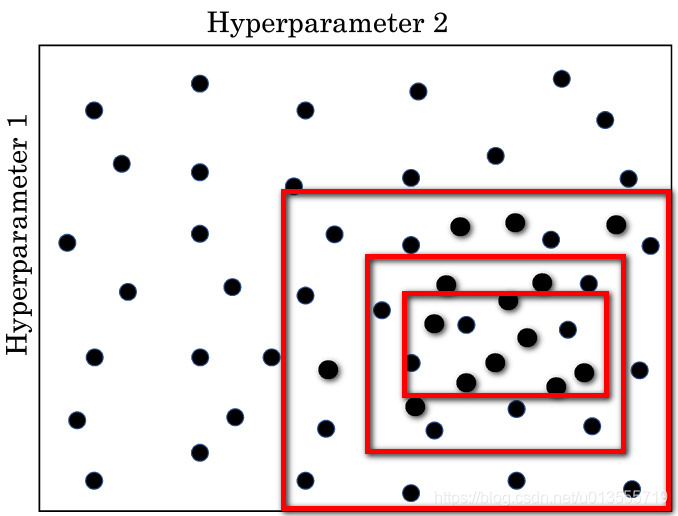
3.2 为超参数选择合适的范围
用对数标尺搜索超参数空间
- 在超参数范围中,随机取值可以提升你的搜索效率,但是随机取值并不是在有效值的范围内的随机均匀取值,而是选择合适的标尺,这对于探究这些超参数很重要
整数范围
- 假设你要选取的隐藏单元的数量的值的数值范围是50 ~ 100中的某点,或者是层数20 ~ 40,只需要平均的随机从20 ~ 40的范围中选取数字即可.
超参数学习率\(\alpha\)
假设你要搜索的学习率的范围在0.0001 ~ 1的范围中
- 如果使用随机均匀取值(即数字出现在0.0001 ~ 1的范围内的概率相等,出现概率均匀)
- 那么使用上述方法,90%的数值会落在0.1 ~ 1之间,结果就是0.1 ~ 1之间,应用了90% 的资源,而在0.0001到1之间,只有10%的搜索资源
- 使用对数标尺搜索超参数的空间更加合理
-
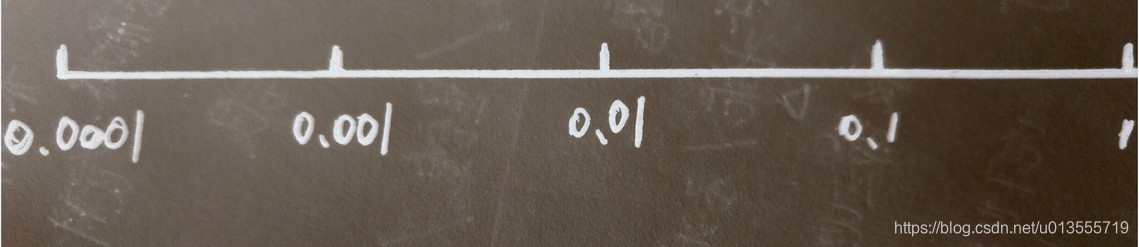
在对数轴上均匀随机取点,这样在0.0001到0.001之间,会有更多的搜索资源可以使用.
-
在python中,你可以这样实现.
- 使r=-4*np.random.rand()[np.random.rand()创建一个给定类型和形状的数组,将其填充到一个均匀分布的随机样本[0,1)中]
- \(\alpha\)随机取值\(\alpha = 10^{r}\),从第一行可以得出\(r\epsilon[-4,0]\),那么\(\alpha在10^{-4}到10^{0}之间\)
-
更常见的是取值范围是\(10^{a} - 10^{b}\)的一个区间,你可以通过\(log_{10}0.0001\)算出a的值即-4.在右边的值是\(10^{b}\),\(log_{10}1=0\)得到b的值是0.
在[a,b]区间随机均匀的给r取值,将超参数设置为\(10^{r}\),这就是在对数轴上取值的过程.
\(\beta\)计算指数加权平均值
- 假设\(\beta = 0.9-0.999\),对于指数加权平均值,若\(\beta\)=0.9即是取10天中的平均值,若\(\beta\)取0.999即是在1000个值中取指数加权平均值.
- 对于\(\beta= 0.9-0.999\)考虑\((1-\beta)即0.001 - 0.1\),所以去\(r\epsilon[-3,-1]\)则这是超参数的随机取值.
- 对于公式\(\frac{1}{1-\beta}\),当\(\beta\)接近于1时,\(\beta\)就会会对细微的变化十分敏感
- \(\beta_{1}=0.9000\rightarrow0.9005,无论\beta_{1}=0.9000还是0.9005对于\frac{1}{1-\beta_{1}}都没有很大影响.\)
- 但是当\(\beta的取值十分接近于1的时候,例如\beta_{2}=0.999\rightarrow0.9995\),\(\frac{1}{1-0.999}=1000\)表示在1000个数据中取平均\(\frac{1}{1-0.9995}=2000\)表示在2000个数据中取平均,很接近1时看似微小的改动都会带来巨大的差异!
