基础排序算法之快速排序(Quick Sort)
快速排序(Quick Sort)同样是使用了分治法的思想,相比于其他的排序方法,它所用到的空间更少,因为其可以实现原地排序。同时如果随机选取中心枢(pivot),它也是一个随机算法。最重要的是,快速排序(Quick sort)的算法分析的过程非常给力。
本文首先描述问题,再说明快速排序(Quick Sort)的基本思路并给出伪代码,之后贴出自己的Python代码。在验证完算法的正确性之后,给出如何选择好的中心枢(pivot)的方法,即随机快速排序(Randomized Quick sort),并贴代码。最后进行算法复杂度分析。
问题描述
问题描述和其他排序算法一样,输入一组未排序的数组,如左边的数组,通过快速排序算法的计算,输出一组正确排序的数组,如右边的数组。

基本思路和伪代码
在给定的数组中选择一个元素作为中心枢(pivot),对数组重排列并分割(Partition),使得位于该中心枢(pivot)左边的元素都小于该元素,右边的元素都大于该元素,之后递归处理左右两组数。
这里值得注意的地方就是,每一次重排列之后,所选择的中心枢(pivot)元素所在的位置,就是最终排序结果中它应该在的位置。
1 QuickSort(array A, length n) 2 if n = 1 return 3 p = choosePivot(A, n) 4 Partition A around p 5 recursively sort 1st part 6 recursively sort 2st part
经过第4行的操作之后,位于左边的所有元素都小于p,而右边的数都大于p。下文中所有中心枢(pivot)元素都用p表示。

基于某一个p来对数组进行分块有两种实现的方法,第一种方法在内存在开辟新的数组,遍历元素组元素,小于p的从头插入数组,大于p的从尾部插入数组,给个例子:

而第二种方法是原地排序,比第一稍微复杂一点。假设p元素总在数组的最前端(不在最前端就让它和最前端的元素交换),将整个数组分为两部分,前半部分为已经和p比较过的元素集,后半部分为没有和p比较过的元素集。其中前半部分又分为小于p和大于p两部分。如图:

那么只要需要两个标记值i和j就可以所有部分分割开。i 标记小于p部分末端元素,j标记大于p部分的末端元素。如下例:
分割(Partition)的伪代码:
Partition(A, l, r) [input=A[l.......r]] p=A[l] i=l+1 for j=l+1 to r if A[j]<p swap A[i] and A[j] i=i+1 swap A[l] and A[i-1]
假设处理的数组长度为N,从伪代码中可以比较容易算出,Partition的时间复杂度为O(N),而且也实现了原地排序。
Python代码
Pivot选取首元素的实现

1 import random 2 3 def quick_sort(datalist,l,r): 4 if l<r-1: 5 q=partition_first(datalist,l,r) 6 datalist=quick_sort(datalist,l,q) 7 datalist=quick_sort(datalist,q+1,r) 8 return datalist 9 else: 10 return datalist 11 12 def partition_first(datalist,l,r): 13 p=datalist[l] 14 i=l+1 15 for j in range(l+1,r): 16 if datalist[j]<p: 17 datalist[i],datalist[j]=datalist[j],datalist[i] 18 i=i+1 19 datalist[l],datalist[i-1]=datalist[i-1],datalist[l] 20 return i-1
验证算法的正确性
用数学归纳法来检验算法的正确性:
P(N)=快速排序(Quick sort)正确排序长度为N的数组。
Claim:无论选择什么p,在N>=1情况下,P(N)总能正确。
证明:
- 第一步:对于N=1时,返回该值。第一步完成。
- 第二步:第二步中只需要证明对于固定的n,如果∀k<n时,P(k)成立,那么P(n)也成立。

- 快速排序基于p进行分割数组时候,p在此次partition中之后,它所在所在的位置,就是最终排序结果中它应该在的位置。如上图所示,k1为1st part的数组长度,k2为2st part的数组长度。根据前面的假设∀k<n都递归成立,所以经过递归之后,整个数组正确排序。(QED!)
选择好的p值(随机快速排序)
首先先看两个例子:
情况1:对于已经排序好的一列数组,每次p值都选择第一个元素,那么算法的运行时间是多少?(n²)
情况2:对于已经排序号的一列数组,每次p值刚刚好是该数组元素的中位数,那么算法的运行时间是多少?Θ(nlgn)
可以看出,算法的性能取决于p值的选取,直觉上,选取随机的p值可以让算法有比较好的表现(这里我自己也没有完全想明白。)。后续的证明可以得出算法的平均时间复杂度为O(nlgn)。
Python代码
随机快速排序 (Randomized Quick sort)的实现

1 import random 2 def partition_random(datalist,l,r): 3 index=random.randint(l,r-1) 4 datalist[l],datalist[index]=datalist[index],datalist[l] 5 p=datalist[l] 6 i=l+1 7 for j in range(l+1,r): 8 if datalist[j]<p: 9 datalist[i],datalist[j]=datalist[j],datalist[i] 10 i=i+1 11 datalist[l],datalist[i-1]=datalist[i-1],datalist[l] 12 return i-1
算法分析
首先,我们先有如下定义:
- 输入数组的长度为定值N;
-
样本空间(Sample Space) Ω为在快速排序中选择中心枢(pivot)元素的所有可能性集合,其中每一个可能性其实就是一个p值的序列。
- 定义一个随即变量(Random Variable) C:对于∀σ∈Ω,C(σ)为在某个可能的p值序列,即某一σ情况下,输入元素相互比较的总次数。
为什么要设置这样一个随机变量?因为算法的运行时间其实主要取决于Partition函数中元素间比较的次数。所以要计算出快速排序(Quick sort)的时间复杂度,也就是要算出该随机变量C的期望值E(C)。
我们假设zi在一组数中,为第i小的数,如下图所示

我们令xij为在某一个p值序列下,zi和zj相互比较的次数之和。那么在执行快速排序(Quick sort)的时候,任意两个元素的比较次数(xij)为多少次?0或1。因为任意两个元素能够比较的前提必须是其中某一个元素被选为中心轴元素(pivot)。不管是两个元素位于p值的同边或异边都将不会在发生比较事件(Event)。
因为 C(σ)=所有输入元素相互比较的次数;xij(σ)=任意两个元素相互比较的次数
所以 
根据期望的线性特性:
 得出:
得出:
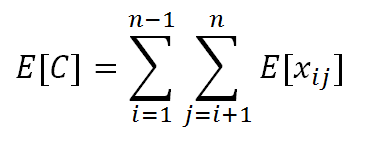
因为:

假定i<j,p[zi,zj发生相互比较的事件]=2/(j-i+1)。(之前已经说过两个数发生比较事件的情况只会在这两个数被选为pivot的时候发生,所以概率为头尾选中的次数除以i,j之间元素的个数)

对于i值而言,并不会超过n种情况,而对于某一固定的i值,有

所以:
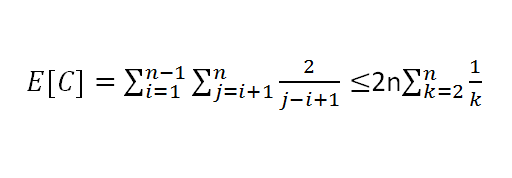
可以看出,后半项是一个调和级数,所以最后:
 E[C]=O(nlgn) QED!
E[C]=O(nlgn) QED!
参考:算法导论以及Tim Roughgarden的讲义
posted on 2013-09-03 12:04 热爱GIS的坏蜀黍 阅读(2019) 评论(0) 编辑 收藏 举报



