第5章 优化程序性能

第5章 优化程序性能

写程序首先要保证它在所有可能的情况下都正确工作，然后才是尽可能地让程序运行得快。

编写高效程序要做到以下几点：

1. 选择适当的算法和数据结构
2. 编写出编译器能够有效优化以转换成高效可执行代码的源代码。（需要理解编译器的能力和局限性）
3. 将一个任务分成多个任务，可以在多核和多处理的某种组合上并行计算。（第12章）

5.1 优化编译器的能力和局限性

编译器向用户提供了编译器所使用的优化的控制。比如gcc，-Og使用基本优化，-O1，-O2，-O3使用更多大量优化。

因为编译器对程序使用安全的优化，所以有一些因素会阻碍优化。

• 内存别名使用，编译器会假设不同指针可能会指向内存中同一个位置。

这里举个栗子。练习题5.1

#include <stdio.h>

int main(){
 long a=4,b=5;
 printf("a=%ld\n",a);
 printf("b=%ld\n",b);
 swap(&a,&a);
 printf("a=%ld\n",a);
 printf("b=%ld\n",b);
 return 0;
}

void swap(long *xp,long *yp)
{
 *xp = *xp + *yp;
 *yp = *xp - *yp;
 *xp = *xp - *yp;
}

可见两个指针指向同一个位置时，程序出错，所以编译器不会自动优化。

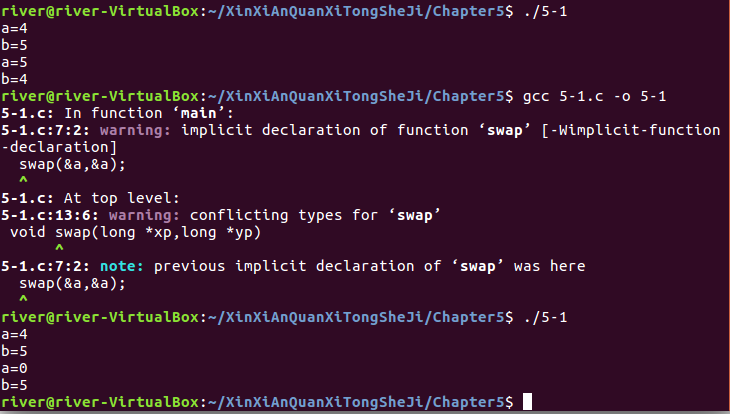
• 函数调用的副作用，编译器会保持所有的函数调用不变。

这里举个例子是，函数内部修改全局变量，改变调用次数会改变函数结果。

比如

long counter =0;

long f(){
    return counter++;
}

long func1(){
    return f()+f()+f()+f();
}

long func2(){
    return 4*f();
}

func1返回6，而func2返回0。

5.2 表示程序性能

度量标准每元素的周期数（CPE），在更细节的级别上度量迭代程序的循环性能。

没看懂CPE到底是怎么度量的。但知道了一种优化前置和计算的优化技术——循环展开。

练习题5.2：

用数学方法，对这3个一次函数画图分析即可。

n<=2时，版本1最快。

3<=n<=7时,版本2最快。

n>=8时，版本3最快。

5.3 程序示例

（说明一个抽象的程序时如何被系统地转换成更有效的代码的）

这一节给出了一个优化示例：一个抽象数组（可定义为整数和浮点数），一个抽象合并运算（可定义为加法和乘法）。代码如下：

combine1

void combine1(vec_ptr v,data_t *dest)
{
    long i;
    
    *dest IDENT;
    for(i=0;i<vec_length(v);i++){
        data_t val;
        get_vec_element(v,i,&val);
        *dest = *dest OP val;
    }
}

在参考机（Intel Core i7 Haswell）上尝试运算和数据类型的不同组合，编译方法使用未优化和-O1的优化。发现-O1显著地提高了程序性能。

5.4 消除循环的低效率

combine1每次循环都要对测试条件求值，同时向量长度也不会随循环的进行改变。所以只需要计算一次向量长度，在每次测试条件中都使用这个计算好的值。改进后的combine2如下：

void combine2(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    
    *dest IDENT;
    for(i=0;i<length;i++){
        data_t val;
        get_vec_element(v,i,&val);
        *dest = *dest OP val;
    }
}

这是一类常见的优化——代码移动，即识别要执行多次但计算结果不会改变的计算，将计算移动到不会被多次求值的地方。

这一节只说明了一个问题，因为编译器进行的是安全的优化，所以，代码移动这样的优化技术需要程序员手动完成，编译器是无法完成这样的优化的。

同时，这个例子说明了一个常见问题：一个看上去无足轻重的代码片断有隐藏的渐近低效率。即小数据集上，性能足够了，但在大型项目中却会变成一个主要的性能瓶颈。

练习题5.3

通过这个练习，让我们认识到循环变量的计算位置，对程序性能有着很大的影响。

对A代码：i被初始化为10（min调用一次），对i判断（max调用一次），i增加（incr调用一次），执行循环体（square调用一次）。再对i判断、增加、执行循环体，直到i等于100，这时max、incr、square调用了90次。i=100后仍然会再去比较（又调用一次max），发现不再符合循环条件，所以不会再调用incr和square。
即：

min	max	incr	square
1	91	90	90

对B代码，我有一个问题，为什么这里对i初始化调用了91，而条件判断只有1次调用。

5.5 减少过程调用

combine2中的代码，每次循环都会调用get_vec_element来获取下一个向量元素。

进一步优化，增加一个函数get_vec_start返回数组的起始地址，循环体内直接通过访问数组，不再每次循环都调用get_vec_element函数。改进后的combine3如下：

void combine3(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    
    *dest IDENT;
    for(i=0;i<length;i++){
        *dest = *dest OP data[i];
    }
}

5.6 消除不必要的内存引用

从汇编代码中可以看出，每次循环，累积变量的值都要从内存中读出，再写入内存。

进一步优化，引入临时变量，用来累积值，只在循环完成后才存回dest。改进后的combine4如下：

void combine4(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(i=0;i<length;i++){
        acc = acc OP data[i];
    }
    *dest = acc;
}

编译器不用自动完成这样的优化，需要程序编写源代码时手动完成。

读到这里，我有一种感觉，程序优化就是不断地减少重复操作，不断减少函数调用，不断减少内存读写（即循环里尽量不用指针）。从combine1到combine4循环体内的代码越来越少

练习题5.4

A.-O2优化：%xmm()存放累积值。-O1优化：%xmm()存放每次循环的乘积临时变量。

B.combine3使用的也是一个变量循环累积，而不是临时变量，所以O2更像combine3的风格。

C.-O2保持了程序的期望行为，因为每次循环读写dest和只在循环开始前后读写是完全一样的。

5.7 理解现代处理器

至此，前面提到的优化技术都不依赖于目标机器的任何特性，想要进一步提高性能，必须考虑利用处理器微体系结构优化，针对不同的目标机进行代码调整。

这一节，主要讲两种下界限制了程序最大性能。

1. 延迟界限：后一条指令必须在前一条指令完全结束后，才能开始。限制了处理器利用指令级并发的能力。
2. 吞吐量界限：处理器功能单元的原始计算能力，这是程序性能的终极限制。

5.7.1 整体操作

主要讲了指令控制单元和执行单元之间的协调合作。各单元的具体功能如下：

• 取值指令块进行分支预测
• 指令译码块将收到的实际程序指令转换成一组微操作。多条指令的不同微操作可以被并行执行。
• 读写内存有加载单元和存储单元实现。
• 分支预测错误时，分支单元开始在新的位置取指。
• 算数运算单元专门用来执行整数和浮点数操作的不同组合。
• 退役单元记录正在进行的处理，并确保它遵循机器级程序的语义。
• 退役单元控制着寄存器文件，只有当指令退役时，程序寄存器才会被更新。

5.7.2 功能单元的性能

算术运算的性能由以下三个量刻画：

1. 延迟：表示完成运算所需要的总时间
2. 发射时间：表示两个连续的同类型的运算之间需要的最小时钟周期数。
3. 容量：表示能够执行该运算的功能单元的数量。

发射时间短是通过流水线实现的，算数运算可以连续地通过各个阶段，而不用等待前一个操作完成后。只有当执行的运算是连续的，逻辑上独立的时候，才能利用这种功能。

我的理解是并发地执行了多条指令的不同阶段，使得每条指令看起来是连续进行的，发射时间为1。

具有多个功能单元的机器可以进一步提高吞吐量。

5.7.3 处理器操作的抽象模型

这一小节，就是想告诉我们不同操作之间的数据相关是如何主宰程序性能的

首先引入程序的数据流表示。在数据流中的寄存器分为只读，只写，局部，循环

然后发现循环寄存器之间的操作链决定了限制性能的数据相关。

在数据流里只提取循环寄存器之间的相关链，这个链的数据相关就是制约性能的关键路径。

继续分析combine4的例子，我们通过分析combine4的关键路径，发现数据相关导致的延迟界限是第二大限制。

我们需要调整操作结构，增强指令级并行性，使得只有第一大主要限制——吞吐量界限。

练习题5.5

一个对多项式求值的函数：

double poly(double a[],double x,long degree)
{
    long i;
    double result = a[0];
    double xpwr = x;
    for(i=1;i<=degree;i++){
        result += a[i]*xpwr;
        xpwr = x*xpwr;
    }
}

A.对于degree=n，循环体被执行n次，每次执行两次乘法，一次加法。所以，一共2n次乘法，n次加法。

B.查询图5-12，浮点数计算的加法延迟是3个周期，乘法延迟是5个周期。

这里我也有一个疑问待解决，为什么对result的更新只需要3个时钟周期，根据数据相关性，应该是8个周期才对呀？书上答案的解释是result更新只需3个周期，xpwr只能在每次迭代中更新需要5个时钟周期。

练习题5.6

5.8 循环展开

承接上一小节，使用k×1循环展开，可以将延迟界限降到1。

那什么是循环展开技术呢？

循环展开就是通过增加每次迭代计算的元素的数量，减少循环的迭代次数。

循环展开能从两方面改进程序性能：

1. 减少不直接有助于程序结果的操作数量。
2. 减少整个计算中关键路径上的操作数量。

通过循环展开得到进一步优化后的combine5：

void combine5(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    long limit = length-1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(i=0;i<limit;i+=2){
        acc =(acc OP data[i]) OP data[i+1];
    }
    
    for(;i<length;i++){
        acc = acc OP data[i];
    }
    
    *dest = acc;
}

5.9 提高并行性

至此，我们的程序性能是受延迟限制的。

因为我们将累计值放在一个单独的变量中，前面的计算完成后，才能进行下一次计算，尽管我们的延迟限制为1，但我们可以打破这种顺序相关，得到更好的性能。

5.9.1 多个累积变量

通过将一组合并运算分割成两个或多个部分，最后合并结果来提高性能。

针对书上的例子，使用的是将偶数位元素和奇数位元素累积在两个变量中（acc0和acc1），将之前的2×1循环展开，改进为2×2循环展开，突破了延迟界限。优化后的combine6如下：

void combine6(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    long limit = length-1;
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    
    for(i=0;i<limit;i+=2){
        acc0 = acc0 OP data[i];
        acc1 = acc1 OP data[i+1];
    }
    
    for(;i<length;i++){
        acc0 = acc0 OP data[i];
    }
    
    *dest = acc0 OP acc1;
}

5.9.2 重新结合变换

重新结合变换：改变元素间的合并顺序

例如：

acc = (acc OP data[i]) OP data[i+1];

重新结合后

acc = acc OP (data[i] OP data[i+1]);

重新结合变化能够减少计算中关键路径上操作的数量，更好地利用功能单元的流水线能力，得到更好的性能。重新结合后的combine7如下：

void combine7(vec_ptr v,data_t *dest)
{
    long i;
    long length = vec_length(v);
    long limit = length-1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    for(i=0;i<limit;i+=2){
        acc = acc OP (data[i] OP data[i+1]);
    }
    
    for(;i<length;i++){
        acc = acc OP data[i];
    }
    
    *dest = acc;
}

5.10 优化合并代码的成果小结

看到这里，我的感受是，通过combine1~7这个不断优化的例子，我们从最开始的程序级的优化技术（比如：代码移动，减少函数引用，减少内存读写），到更深入的机器级优化，从大到小的视野，层层剖析，步步深入，看到了处理器的工作机制，以及从处理器这样的机制引出的优化技术（循环展开，并行累积，重新结合变换）

5.11 一些限制因素

除了延迟限制和吞吐量限制这两个主要因素，还有其他一些限制程序性能的因素。

5.11.1 寄存器溢出

书中提到的寄存器溢出针对的是并行积累技术。
如果循环变量超过了可用寄存器数量，程序就必须在栈上分配一些变量，程序需要在内存中读取变量，并行积累的优势就可能消失。

但对x86-64有足够多的寄存器，在出现寄存器溢出之前就将达到吞吐量限制。

更广泛的定义：寄存器溢出（Register spilling）发生在一个程序编辑之间，在那里有多于寄存器能够保存的活动变量。当一个编译器产生机器代码和有多于这台机器已经寄存的活动变量时，它不得不从寄存器到内存转换或“溢出”一些变量。这以特定的成本发生，因此从内存的访问典型地比从寄存器的访问慢。

5.11.2 分支预测和预测错误处罚

我们已经知道处理器采用分支预测和投机执行的方法处理分支。预测错误需要重新取值计算，引起预测错误处罚。

这里找到一个分支预测错误而引起处罚的例子：浅谈分支预测、流水线与条件转移

程序员遵循以下两个原则，可以尽可能地保证分支预测处罚不会阻碍程序效率。

1. 不要过分关心可预测的分支
2. 书写适合用条件传送实现的代码

5.12 理解内存性能

这一节研究涉及加载和存储操作的程序的性能，只考虑所有数据都存放在高速缓存中。

5.12.1 加载的性能

包含加载操作的程序的性能由两点决定：

1. 流水线的能力
2. 加载单元的延迟

加载操作的延迟可以通过构造一个由一系列加载操作组成的一个计算。比如计算链表长度的函数。

typedef struct ELE {
    struct ELE *next;
    long data;
}list_ele,*list_ptr;

long list_len(list_ptr ls){
    long len = 0;
    while(ls){
        len++;
        ls = ls->next;
    }
    return len;
}

每个时钟周期开始一个操作。

5.12.2 存储的性能

每个时钟周期可以开始一个操作。举个栗子，一个循环只是不停存取，而不做任何计算：

void clear_array(long *dest,long n){
    long i;
    for(i=0;i<n;i++)
      dest[i]=0;
}

测试结果为CPE=1，可见存储操作是完全流水线化的工作模式。

存储操作不会产生数据相关，只有加载操作会收存储操作的影响。

内存操作的实现包括许多细微之处：只有到计算出加载和存储的地址被计算出来以后，处理器才能确定哪些指令会影响其他的指令。

5.13 应用：性能提高技术

优化程序性能的基本策略：

1. 高级设计，使用适当的算法和数据结构
2. 基本编码原则：

• 消除连续的函数调用
• 消除不必要的内存引用

3. 低级优化

• 展开循环
• 通过使用例如多个累积变量和重新结合等技术
• 用功能性的风格重写条件操作

注意：优化中必须保证程序的正确性！

5.14 确认和消除性能瓶颈

这节介绍：

• 使用代码剖析程序
• 系统优化的通用原则——Amdahl定律

5.14.1 程序剖析

Unix提供了一个剖析程序GPROF，使用GPROF有3个步骤:

1. 程序必须为剖析而编译和链接。

gcc -Og -pg prog.c -o prog

2. 程序正常执行

./prog file.txt

产生一个gmon.out的文件
3. 调用GPROF

gprof prog

得到的剖析报告会列出执行各个函数花费的时间，和函数调用历史。这些信息帮助我们了解程序的动态行为。

GPROF有些需要注意的地方：

1. 计时不是很准确
2. 假设没有执行内联替换，则调用信息相当可靠。
3. 默认情况下，不会显示对库函数的计时。

5.14.2 使用剖析程序来指导优化

这一节通过一个示例（一个分析文本文档的n-gram统计信息的应用）向我们说明如何利用剖析程序来指导优化。

Amdahl定律：当我们对系统的某个部分加速时，其对系统整体性能的影响取决于该部分的重要性和加速程度。

5.15 小结

虽然这一章主要在讲述编译器是如何优化的。但对程序员而言还是有两点需要注意：

1. 选择好的算法和数据结构
2. 保持好的编程习惯，避免阻碍优化的因素。

这一章我对处理器体系结构有了了解，以及一系列优化技术。

最后对大程序的优化处理，掌握了剖析工具和分析方法。