之前简要地介绍了一下线性判别函数的的基本性质,接下来我们进行更加详细的讨论。
文中大部分公式和图表来自 MLPP 和 PRML
我们将样本的分布用多元正态分布来近似,为了更加了解这个表达式的含义,我们对协方差矩阵做特征值分解,即Σ = UΛUT
然后将协方差矩阵的逆用同样方法分解,即

代入多元正态分布的模型中,能够得到

这个公式应该很熟悉了,当等式右边取一个常数时就是椭圆的表达形式。以相同的等高线定义的距离的叫做马氏距离(Mahalanobis distance)。可以看出,我们熟悉的欧式距离就是马氏距离的一种特殊的形式。
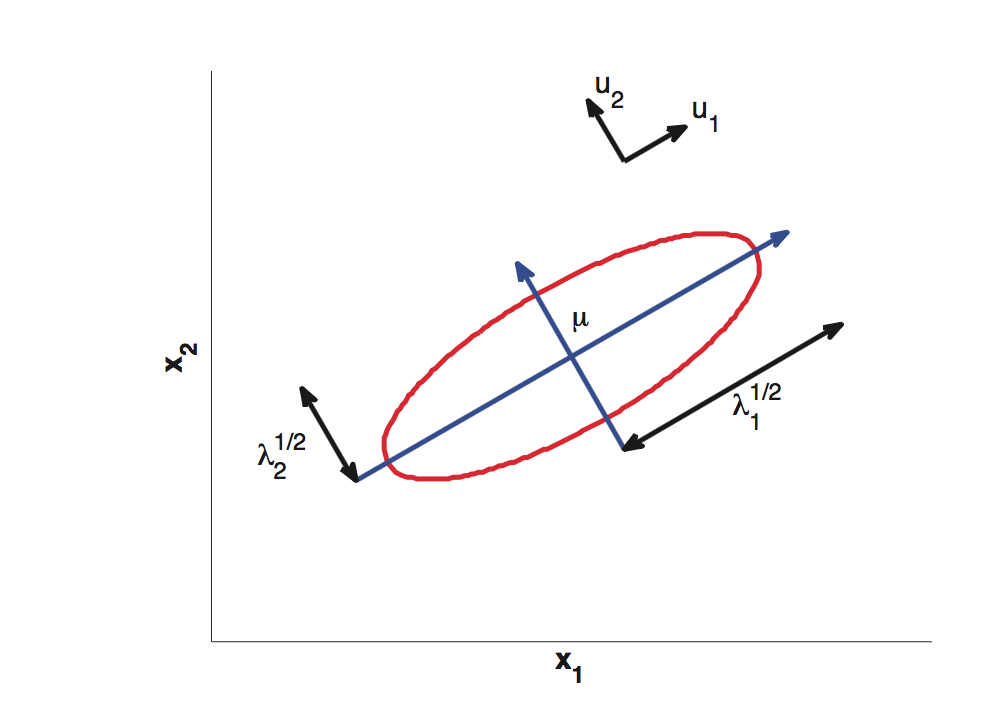
我个人的理解是,马氏距离相当于通过样本之间的协方差对欧式距离做了一个变换,使得距离被“归一化”能够更加准确地反映样本之间的差异关系,否则可能因为量纲问题导致结果的不准确。以上图为例,假设我们要探究薪水和身高的关系,X1代表薪水,X2代表身高。很显然等高线在X1方向会“狭长”很多。如果用欧式距离的话,(5010,180)和(5000,190)对(5000,180)是等距离的,但这个显然不符合逻辑。而用马氏距离就能够解决这个问题。
样本类均值的极大似然估计是样本的平均向量,而协方差矩阵的极大似然估计是样本的协方差矩阵。

这个公式的推导要用到trace trick, 在此不做详述。值得注意的是,这个极大似然估计是有偏的,通常用一种无偏估计来代替,即n分之一分母变成n-1。
那么用高斯分布来近似密度函数的意义是什么呢?原因在于高斯分布是满足最大熵条件的。定义一个连续分布的信息熵(也叫微分熵)如下:
![]()
学过物理的同学都知道,熵是一种无序的程度的度量。将这个概念类比过来,对于随机变量来说,信息熵就代表着不确定性。当一个随机变量很确定取到某一特定的值时,它的信息熵会很低。反之,当它取值很分散时,信息熵会很高。
现在假设我们已知一个随机变量的均值和方差,希望求得在最大熵条件下的密度函数。这个问题可以转化成优化问题,其中限制条件为:

运用拉格朗日乘子法,我们可以得出,高斯分布的信息熵最大。
换句话说,虽然拥有相同均值和方差的分布有很多个,但高斯分布带来了最少的附加条件,包含的信息量最大,因此也更加能够准确地概括所有的情况。这也是我们在不知道分布类型的情况下,选择正态分布的原因。
接下来我们具体分析一下LDA的算法。
在判别函数的公式中,令

考虑2个类别的情况,分为正类的概率可以表示为

将公式变形:

定义:

最后我们可以得到:
![]()
这个公式可以很清楚地看出LDA和逻辑回归的紧密关系。对于LDA来说,判别的依据就是:将x减去x0后,将其投影到线段w上,然后观测大小。下图为协方差矩阵为单位阵时的图示。

另外,从公式可以看出先验概率的影响。当类1的先验概率增加时,x0向类0的方向移动,那么x-x0在类1方向上投影增加,也就以更大的概率取到类1。


