《大话数据结构》第9章 排序 9.2 排序的基本概念与分类
9.2 排序的基本概念与分类
9.2.1 排序的定义
排序是我们生活中经常会面对的问题。同学们做操时会按照从矮到高排列;老师查看上课出勤情况时,会按学生学号顺序点名;高考录取时,会按成绩总分降序依次录取等。那排序的严格定义是什么呢?
假设含有n个记录的序列为{r1,r2,……,rn},其相应的关键字分别为{k1,k2,……,kn},需确定1,2,……,n的一种排列p1,p2,……,pn,使其相应的关键字满足kp1≤kp2≤……≤kpn(非递减或非递增)关系,即使得序列成为一个按关键字有序的序列{rp1,rp2,……,rpn},这样的操作就称为排序。
注意我们在排序问题中,通常将数据元素称为记录。显然我们输入的是一个记录集合,输出的也是一个记录集合,所以说,可以将排序看成是线性表的一种操作。
排序的依据是关键字之间的大小关系,那么,对同一个记录集合,针对不同的关键字进行排序,可以得到不同序列。
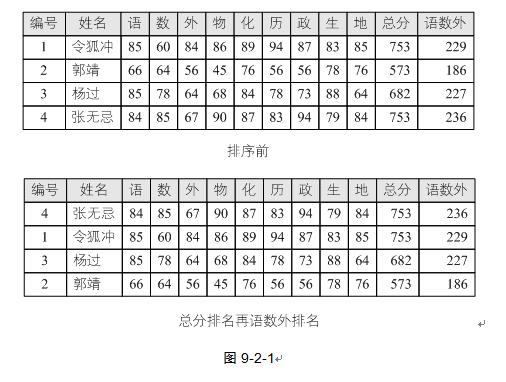
这里关键字ki可以是记录r的主关键字,也可以是次关键字,甚至是若干数据项的组合。比如我们某些大学为了选拔在主科上更优秀的学生,要求对所有学生的所有科目总分降序排名,并且在同样总分的情况下将语数外总分做降序排名。这就是对总分和语数外总分两个次关键字的的组合排序。如图9-2-1,对于组合排序的问题,当然可以先排序总分,若总分相等的情况下,再排序语数外总分,但这是比较土的办法。我们还可以应用一个技巧来实现一次排序即完成组合排序问题,例如把总分与语数外都当成字符串首尾连接在一起(注意语数外总分如果位数不够三位需要在前面补零),很容易可以得到令狐冲的“753229”要小于张无忌的“753236”,于是张无忌就排在了令狐冲的前面。
9.2.2 排序的稳定性
也正是由于排序不仅是针对主关键字,那么对于次关键字,因为待排序的记录序列中可能存在两个或两个以上的关键字相等的记录,排序结果可能会存在不唯一的情况,我们给出了稳定与不稳定排序的定义。
假设ki=kj(1≤i≤n,1≤j≤n,i≠j),且在排序前的序列中ri领先于rj(即i<j)。如果排序后ri仍领先于rj,则称所用的排序方法是稳定的;反之,若可能使得排序后的序列中rj领先ri,则称所用的排序方法是不稳定的。如图9-2-2,经过对总分的降序排序后,总分高的排在前列。此时对于令狐冲和张无忌而言,未排序时是令狐冲在前,那么它们总分排序后,分数相等的令狐冲依然应该在前,这样才算是稳定的排序,如果他们二者颠倒了,则此排序是不稳定的了。只要有一组关键字实例发生类似情况,就可认为此排序方法是不稳定的。排序算法是否稳定的,要通过分析后才能得出。

9.2.3 内排序与外排序
根据在排序过程中待排序的记录是否全部被放置在内存中,排序分为:内排序和外排序。
内排序是在排序整个过程中,待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。我们这里主要就介绍内排序的多种方法。
对于内排序来说,排序算法的性能主要是受三个方面影响
1) 时间性能。排序是数据处理中经常执行的一种操作,往往属于系统的核心部分,因此排序算法的时间开销是衡量其好坏的最重要的标志。在内排序中,主要进行两种操作:比较和移动。比较指关键字之间的比较,这是要做排序最起码的操作。移动指记录从一个位置移动到另一个位置,事实上,移动可以通过改为记录的存储方式来予以避免(这个我们在讲解具体的算法时再谈)。总之,高效率的内排序算法应该是具有尽可能少的关键字比较次数和尽可能少的记录移动次数。
2) 辅助空间。评价排序算法的另一个主要标准是执行算法所需要的辅助存储空间。辅助存储空间是除了存放待排序所占用的存储空间之外,执行算法所需要的其他存储空间。
3) 算法的复杂性。注意这里指的是算法本身的复杂度,而不是指算法的时间复杂度。显然算法过于复杂也会影响排序的性能。
根据排序过程中借助的主要操作,我们把内排序分为:插入排序、交换排序、选择排序和归并排序。可以说,这些都是比较成熟的排序技术,已经被广泛地应用于许许多多的程序语言或数据库当中,甚至它们都已经封装了关于排序算法的实现代码。因此,我们学习这些排序算法的目的更多原因并不是为了去在现实中编程排序算法,而是通过学习来提高我们编写算法的能力,以便于去解决更多复杂和灵活的应用性问题。
本章一共要讲解七种排序的算法,按照算法的复杂度分为两大类,冒泡排序、简单选择排序和直接插入排序属于简单算法,而希尔排序、堆排序、归并排序、快速排序属于改进算法。后面我们将依次讲解。
9.2.4 排序用到的结构与函数
为了讲清楚排序算法的代码,我先提供一个用于排序用的顺序表结构,此结构也将用于之后我们要讲的所有排序算法。
typedef struct
{
int r[MAXSIZE+1]; /* 用于存储要排序数组,r[0]用作哨兵或临时变量 */
int length; /* 用于记录顺序表的长度 */
}SqList;
另外,由于排序最最常用到操作是数组两元素的交换,我们将它写成函数,在之后的讲解中会大量的用到。
void swap(SqList *L,int i,int j)
{
int temp=L->r[i];
L->r[i]=L->r[j];
L->r[j]=temp;
}
好了,说了这么多,我们来看第一个排序算法。




