测度论：Measure Theory (1)

这是我的笔记以及一些个人理解，其中大多证明系本人完成。

---

Notations

1. $\mathbb{N} = \left\{0, 1,2,\ldots\right\}$ - 自然数集
2. $\mathbb{Z} = \left\{\ldots,-2, -1,0,1,2,\ldots \right\}$ - 整数集
3. $\mathbb{Q} = \left\{ \frac{m}{n}: m, n \in \mathbb{Z}, n \neq 0\right\}$ - 有理数集
4. $\mathbb{R}$ - 实数集
5. $\mathbb{R}^{n} = \left\{ (x_{1}, x_{2}, \ldots, x_{n}): x_{i} \in \mathbb{R} \mbox{ for }1 \leq i \leq n\right\}$
6. Set membership: 若 $x \in A$ ，则称 $x$ 是集合 $A$ 的一个元素(element)
7. Set inclusion: $\forall a \in A: a \in B \iff A \subset B$ ; $A = B \iff A \subset B, B \subset A$
8. Intersection: $A \cap B := \left\{x: x\in A \mbox{ and } x\in B \right\}$
9. Union: $A \cup B := \left\{x: x \in A \mbox{ or } x \in B \right\}$
10. Difference: $A \setminus B := \left\{x \in A: x \notin B\right\}$
11. Complement: $A^{c} := \Omega \setminus A$ ，其中 $\Omega$ 定义为全集
12. Symmetric complement: $A \Delta B := (A \setminus B) \cup (B \setminus A)$

---

Russell's Paradox*

有的时候一个集合可以将自己作为元素，e.g. $E = \ldots\left\{\left\{\left\{ 3 \right\}\right\}\right\} \ldots$，可以发现$E \in E$。

设集合 $\mathcal{F}:= \left\{ X: \mathcal{F} \notin X \right\}$ 为所有不包含其自身作为元素的集合构成的集类，例如 $\left\{1, 2, 4 \right\} \in \mathcal{F}$, $\left\{a, b, c, d\right\} \in \mathcal{F}$, 但 $E \notin \mathcal{F}$ 。那么 $\mathcal{F}$ 是它自己的一个元素吗？

这种定义方式会产生悖论：假设 $\mathcal{F} \in \mathcal{F}$，那么 $\mathcal{F} \notin \mathcal{F}$ ;而假设 $\mathcal{F} \notin \mathcal{F}$，则 $\mathcal{F} \in \mathcal{F}$ 。这种集合的构造方式与集合论公理系统产生了矛盾，故如此构造的集合接下来将被排除在讨论范围之外。

---

假设我们有集合 $A_{1}, A_{2}, A_{3}, \ldots$ ，考虑以下两个集合：
Countable intersections: $X := \bigcap\limits^{\infty}_{n=1}A_{n} = A_{1} \cap A_{2} \cap A_{3} \cap \ldots$

Countable unions: $Y := \bigcup\limits^{\infty}_{n=1}A_{n} = A_{1} \cup A_{2} \cup A_{3} \cup \ldots$

实际上，以上写法可以推广到更普遍的形式，对于collection of indices $\Lambda$:

$$\bigcap\limits_{\alpha\in\Lambda}A_{\alpha} = \left\{ x: \forall \alpha \in \Lambda, x \in A_{\alpha}\right\}\\ \bigcup\limits_{\alpha\in\Lambda}A_{\alpha} = \left\{ x: \exists \alpha \in \Lambda, x \in A_{\alpha}\right\}$$

注意，上面两种写法分别为集合序列$\left\{ A \right\}^{\infty}_{n=1}$的可数交与可数并，也就是说为可数无穷的集合的交或并。而下面的两种写法中由于$\Lambda$不必为可数集，则$\left\{ A_{\alpha}\right\}_{a\in\Lambda}$也不必为可数，因此可以代表不可数无穷的集合的交或并。然而无论是可数还是不可数无穷，始终有：

$$x \in \bigcap\limits_{\alpha\in\Lambda}A_{\alpha} \implies \forall \alpha \in \Lambda: x \in A_{\alpha}\\ x \in \bigcup\limits_{\alpha\in\Lambda}A_{\alpha} \implies \exists \alpha \in \Lambda: x \in A_{\alpha}$$

为什么要强调这看似显而易见的这一点，当时在某个证明中，恰恰是这个简单的问题给初学者的我造成了一些困扰。例如一些看似能类比而实则不能的情况，例如以下这个例子：

Example 1.1

令$\left\{A_{n}\right\}_{n\in\mathbb{N}}$ 为一个集合序列，such that:

$$\begin{align*} A_{0} &= \left\{\left\{0\right\}\right\},\\ A_{1} &= \left\{\left\{0\right\}, \left\{0, 1\right\}\right\},\\ A_{2} &= \left\{\left\{0\right\}, \left\{0, 1\right\}, \left\{0,1,2\right\}\right\},\\ &\vdots\\ A_n &= \{\{0\}, \{0,1\},\dots, \{0,1,2,\dots, n\}\}\\ &\vdots \end{align*}$$

那么自然数集是否属于这个序列的可数并呢？(i.e. $\mathbb{N} \in \bigcup\limits_{n\in\mathbb{N}}A_{n}$ ?)

以下是当时我的困扰。
首先，很容易可以证明$\mathbb{N} = \bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\}$：

$\Longrightarrow$：对于任意的$k \in \mathbb{N}$，有$k \in \left\{0,1,...,k\right\} \subset \bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\}$，那么$\mathbb{N} \subset \bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\}$。

$\Longleftarrow$：Conversely，可数并 $\bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\}$中的任意一项的元素都为自然数，那么可数并$\bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\}$的元素也都为自然数（若认为这个证明不够完美，可以用反证，即假设可数并中存在一个不为自然数的元素...），那么$\bigcup\limits_{n\in\mathbb{N}}\left\{0,1,...,n\right\} \subset \mathbb{N}$。

因此，如果我们能通过集合的可数无穷并与归纳（induction）的方法定义自然数集$\mathbb{N}$，为什么不能用类似的方法证明以上的关系（i.e. $\mathbb{N} \in \bigcup\limits_{n\in\mathbb{N}}A_{n}$）呢？

因为如果这个关系得以成立，那么存在$n_{0} \in \mathbb{N}$，such that $\mathbb{N} \in A_{n_{0}}$。但是任意的$A_{n}$都是有限的，而$\mathbb{N}$是无限的。

---

De Morgan's Laws

$$\left(\bigcup\limits_{\alpha}A_{\alpha} \right)^{c} = \bigcap\limits_{\alpha}A^{c}_{\alpha}\\ \left(\bigcup\limits_{\alpha}A_{\alpha} \right)^{c} = \bigcap\limits_{\alpha}A^{c}_{\alpha}\ $$

---

Example 1.2

(The intersection of open sets can be a closed set.)

$$\begin{align*} & A_{1} = \left(-1,2\right)\\ & A_{2} = \left(-\frac{1}{2}, 1+\frac{1}{2}\right) \\ & \vdots\\ & A_{n}=\left(-\frac{1}{n}, 1+\frac{1}{n}\right) \\ & \vdots\\ \end{align*}$$

We have $\bigcap\limits_{n\in\mathbb{N}}A_{n}=[0, 1]$.

---

Proof. (Example 1.2)

Firstly，for $\forall x \in [0,1]$，since $-\frac{1}{n} < 0 \leq x \leq 1 < 1+\frac{1}{n}$，then for $\forall n \in \mathbb{N}$，we have $x\in A_{n}$, hence $x \in \bigcap\limits_{n\in\mathbb{N}}A_{n}$。

Conversely，suppose $\exists x \in \bigcap\limits_{n\in\mathbb{N}}A_{n}$，such that $x \notin [0,1]$，i.e., $x\in (-\infty, 0) \cup (1, \infty)$. W.l.o.g., suppose $x \in (1, \infty)$, 则$\exists \epsilon > 0$，such that $x = 1 + \epsilon$。However, for $\forall \epsilon > 0$，let $n = \lceil \frac{1}{\epsilon} \rceil + 1 \geq 1$，then we must have $0 < \frac{1}{n} < \epsilon \implies 1 < 1 + \frac{1}{n} < 1 + \epsilon$。This means for $\forall x \in (1, \infty)$，there exists $A_{n}=\left(-\frac{1}{n}, 1+\frac{1}{n}\right)$，such that $x \notin A_{n} \implies x \notin \bigcap\limits_{n\in\mathbb{N}}A_{n}$, this produces contradiction. Similarly, there is contradicition when $x \in (-\infty, 0)$. Therefore, $\forall x \in \bigcap\limits_{n\in\mathbb{N}}A_{n}: x \in [0,1]$.

---

Definition. Cartisian product

The Cartisian product (笛卡尔积) $A \times B$ of sets $A$ and $B$ is the set of all ordered pairs defined as:

$$A \times B := \left\{ (a, b): a \in A, b \in B \right\}$$

---

Definition. Indicator function

The intercator function（指示函数) $\mathbb{I}_{A}$ of set $A$ is the function defined as:

$$\mathbb{I}_{A}(x):= \begin{cases} 1 & \mbox{if } x \in A\\ 0 & \mbox{if } x \notin A \end{cases}$$

---

Noted that $\mathbb{I}_{A \cap B} = \mathbb{I}_{A} \cdot \mathbb{I}_{B}$, $\mathbb{I}_{A \cup B} = \mathbb{I}_{A} + \mathbb{I}_{B} - \mathbb{I}_{A}\mathbb{I}_{B}$, $\mathbb{I}_{A^{c}} = 1 - \mathbb{I}_{A}$.

Definition. Countability and Cardinality

Set $A$ is called countable （可数的）or denumerable （可列的）if there is a one-to-one mapping between $A$ and a subset of $\mathbb{N}$.

---

Noted that it should be the "subset of $\mathbb{N}$" here, instead of $\mathbb{N}$ itself. Otherwise, there is no one-to-one relationship between the set $\left\{ 1, 2, 3\right\}$ and $\mathbb{N}$ for instance, while the former is countable apparently.

Two sets $A$ and $B$ are said to have the same cardinality (基数，或势) if there is a one-to-one mapping between $A$ and $B$.

If there is no one-to-one correspondence between sets $A$ and $B$, then we say, the cardinality of $B$ is bigger that of $A$.

Example 1.3

由上述定义，我们可以称偶数和自然数“一样多”（等势）。

Assume the set of all even numbers to be $A:= \left\{ 0, 2, 4, 6, \ldots\right\}$，then there is a one-to-one mapping：$f: A \rightarrow \mathbb{N}, x \longmapsto \frac{1}{2}x$。

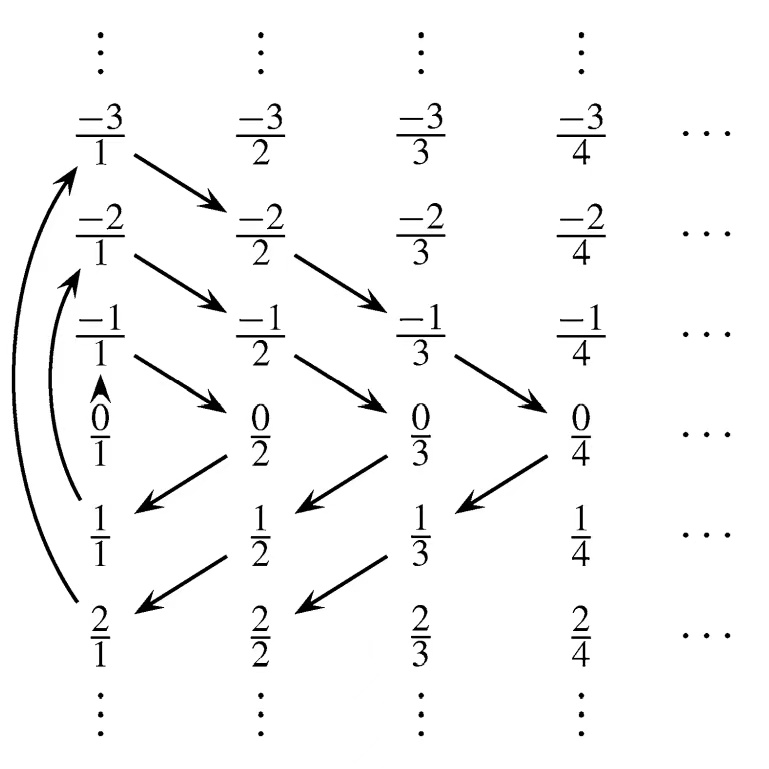
Indeed, we can show the countability of the set of all rational numbers $\mathbb{Q}$ intuitively by the following construction:
$\frac{0}{1}, \frac{-1}{1}, \frac{0}{2}, \frac{1}{1}, \frac{-2}{1}, \frac{-1}{2}, \frac{0}{3} \frac{1}{2}, \frac{2}{1}, \frac{-3}{1}, \frac{-2}{2}, \frac{-1}{3}, \frac{0}{4}, \frac{1}{3}, \frac{2}{2}, \frac{3}{1}, \ldots$

Notice the way we listed all rational numbers:

• Numerator：

$$\begin{align*} &0;\\ -&1, 0, 1;\\ -&2, -1, 0, 1, 2;\\ -&3, -2, -1, 0, 1, 2, 3;\\ \cdots \end{align*}$$

• Denominator：

$$\begin{align*} &1;\\ &1, 2, 1;\\ &1, 2, 3, 2, 1;\\ &1, 2, 3, 4, 3, 2, 1;\\ \cdots \end{align*}$$

Or more intuitively,

Example 1.4 (Uncountability of $(0, 1]$)

Cantor证明了集合$(0, 1]$不可列。我们可以将$(0, 1]$上的实数以小数的形式写下来：

$$\begin{align*} &x_{1} = 0.a_{1,1}a_{1,2}a_{1,3} \cdots\\ &x_{2} = 0.a_{2,1}a_{2,2}a_{2,3} \cdots\\ &x_{3} = 0.a_{3,1}a_{3,2}a_{3,3} \cdots\\ &\vdots \end{align*}$$

其中，$a_{i, j} \in \left\{0, 1, \ldots, 8, 9\right\}$ for $\forall i,j \in \mathbb{Z}^{+}$。

假设它与$\mathbb{N}$之间存在一一映射关系。但是，我们总可以找到这么一个$x \in (0, 1)$：

$$x = 0.b_{1}b_{2}b_{3}\cdots$$

其中$b_{k} \neq a_{k, k}$ for $\forall k \in \mathbb{Z}^{+}, b_{k} \in \left\{0, 1, \ldots, 8, 9\right\}$。
i.e., $b_{1} \neq a_{1, 1}, b_{2} \neq a_{2, 2}, b_{3} \neq a_{3, 3}, \ldots$

那么，如此构造的$x \in (0, 1]$不等于以上任何一个数$x_{1}, x_{2}, \ldots$，也就是说，无论我们如何构造此一一映射，总能找到一个数$x \in (0, 1]$破坏该映射（使一一映射不成立），即$(0, 1]$ 与 $\mathbb{N}$之间不存在一一映射关系，所以$(0, 1]$不可数。

Example 1.5

The cardinality of $(0, 1)$ is the same as the cardinality of $\mathbb{R}$, since we can construct a mapping:

$$f: (0, 1) \rightarrow \mathbb{R}, x \longmapsto \tan(\pi x - \frac{\pi}{2})$$

Theorem 1.1 (Cantor)

For an arbitrary set $X$, there is no one-to-one correspondence between X and Y = 2^{X} (the power set of X).

---

Proof. (Theorem 1.1 Cantor)

Suppose there exists a one-to-one mapping $\varphi: X \rightarrow Y = 2^{X}$, where $Y$ is the power set of $X$.

We know that $\varphi$ is surjective by one-to-one mapping relationship. Then we have:

$$\forall Z \in Y=2^{X}: \exists z \in X: \varphi(z)=Z$$

Since $Y$ is the power set of $X$, that is, $Y$ contains all subsets of $X$, then $Z \subset X$. Now, we try to disprove the assumption of surjective relationship.

Define $Z:= \left\{z \in X: z \notin \varphi(z) \right\}$, that is, for any element $z \in Z \subset X$, $z$ is not contained in $\varphi(z)$. $Z$ is a subset of $X$, so $Z \in Y$. Furthermore, by our surjective assumption: $\exists z_{0} \in X: \varphi(z_{0}) = Z \in Y$. However,

• If $z_{0} \in Z$, according to the way we contructed $Z$, we have $z_{0} \notin \varphi(z_{0})$. We have $\varphi(z_{0}) = Z$ above, then $z_{0} \notin Z$, which shows contradiction.

• If $z_{0} \notin Z$, we must have $z_{0} \in \varphi(z_{0})$. This is because if $z_{0} \notin \varphi(z_{0})$, by the way how $Z$ was constructed, we would otherwise have $z_{0} \in Z$. Since $\varphi(z_{0}) = Z$, there would be contradiction again.

We can conclude from the above that:

$$\forall z \in X: \varphi(z) \neq Z,$$

which contradicts to our assumption of surjection. Therefore, there exists no surjection from $X$ to $2^{X}$, and thus exists no one-to-one mapping $X \rightarrow 2^{X}$.

Corollary 1.1

If $Y$ is the power set of $X$ (i.e. $Y = 2^{X}$), then the cardinality of $Y$ is bigger than the cardinality of $X$ (i.e. $|Y| > |X|$).

---

Proof. (Corollary 1.1)

We shown that there exists no one-to-one mapping between $X$ and $Y$ in Theorem 1.1 above. However, since $Y$ is the power set of $X$, then for $\forall x \in X: \left\{x\right\} \in Y$, so that we can form a one-to-one mapping between $X$ and $A:= \left\{ \left\{ x\right\}: x\in X \right\} \subset Y$ (i.e. A is the set which contains all singletons of X). By definition, we conclude that $|Y| > |X|$.

---

Definition. ($\sigma-$fields)

A family $\mathcal{F}$ of subsets of a universal set $\Omega$ is clled $\sigma-$field (or $\sigma-$algebra) if the following conditions hold:

1. $\Omega \in \mathcal{F}$
2. If $A \in \mathcal{F}$, then $A^{c} \in \mathcal{F}$.
   (Closed under complement)
3. If $A_{n} \in \mathcal{F}$ for all $n = 1, 2, \ldots$, then $\bigcup\limits^{\infty}_{n=1}A_{n} \in \mathcal{F}$.
   (Closed under countable unions)

---

Definition.

Let $A$ be an family of subsets of $\Omega$, then there exists a unique smallest $\sigma-$field $\mathcal{F}_{A}$ that contains every set in $A$, which is called the $\sigma-$field generated by A.

Let $\Omega = \mathbb{R}$, then the minimal $\sigma-$field containing all open intervals $(a, b)$ is called Borel $\sigma-$field, normally denoted by $\mathcal{B} = \mathcal{B}(\mathbb{R}) = \mathcal{B}_{\mathbb{R}}$.

---

Notice a tricky example here. The word "contain" means "$\in$" mathematically. Therefore, for example, we should say the $\sigma-$field generated by $\left\{ \left\{ 1 \right\} \right\}$ instead of $\left\{1\right\}$.

---

Definition. (Fields)

A family $\mathcal{A}$ of subsets of a universal set $\Omega$ is called a field if the following conditions hold:

1. $\Omega \in \mathcal{A}$
2. $\forall A, B \in \mathcal{A} : A \cup B$, $A \setminus B \in \mathcal{A}$
   (Equivalently: $\forall A, B \in \mathcal{A}: A \cup B \in \mathcal{A}$ and $\forall A \in \mathcal{A}: A ^{c} \in \mathcal{A}$)

---

Proof. (Equivalent conditions of Fields)

$\Longrightarrow$ Suppose $\forall A, B \in \mathcal{A}: A \cup B$, $A \setminus B \in \mathcal{A}$. Since $\Omega \in \mathcal{A}$, then $A^{c} = \Omega\setminus A \in \mathcal{A}$.

$\Longleftarrow$ Suppose $\forall A, B \in \mathcal{A}: A \cup B \in \mathcal{A}$, and $\forall A \in \mathcal{A}: A^{c} \in \mathcal{A}$. For $A, B \in \mathcal{A}$, we have $A \setminus B = A \cap B^{c} = \left( A^{c} \cup B \right)^c$. By assumption, $A \in \mathcal{A}$ indicates $A^{c} \in \mathcal{A}$, so $\left( A^{c} \cup B \right) = \left( A^{c} \cup B \right)^c \in \mathcal{A}$, hence $A \setminus B \in \mathcal{A}$.

Example 1.6

Let $\Omega = \mathbb{R}$ and consider the family of subsets:

$$\mathcal{A}:= \left\{A \subset \Omega: A\mbox{ or } A^{c} \mbox{ is finite or empty} \right\}$$

Proof that $\mathcal{A}$ is a field but not a $\sigma-$field.

Proof. (Example 1.6)

First of all, $\empty$ is empty, so that $\empty^{c} = \Omega \in \mathcal{A}$.

Suppose for arbitrary non-empty sets $A, B \subset \Omega$, where $A, B \neq \Omega$ and $A, B \in \mathcal{A}$, and one of $A, A^{c}$ is finite, one of $B, B^{c}$ is finite (cannot be finite simultaneously).

1. Suppose $A, B$ are finite. Then $A \cup B$ is finite $\implies A \cup B \in \mathcal{A}$. Besides, $A \setminus B = \left(A \cap B^{c}\right) \subset A$ is finite or empty $\implies A \setminus B \in \mathcal{A}$.

2. Suppose $A, B$ are infinite. Then $A^{c}, B^{c}$ are finite, and so is $A^{c} \cap B^{c}$. Then $A^{c} \cap B^{c} \in \mathcal{A} \implies \left(A^{c} \cap B^{c}\right)^{c} = \left(A \cup B\right) \in \mathcal{A}$. Moreover, $A \setminus B = \left(A \cap B^{c}\right) \subset B^{c}$ where $B^{c}$ is finite, thus $A \setminus B \in \mathcal{A}$.

3. W.l.o.g., suppose $A$ is infinite, $B$ is finite. Then $A^{c}$ is finite, and so is $A^{c} \cap B^{c}$. Hence $A \cup B = \left( A^{c} \cap B^{c} \right)^{c} \in \mathcal{A}$. Furthermore, $A^{c}$ and $B$ are finite and so is $A^{c} \cup B$. Therefore $A \setminus B = \left(A^{c} \cup B\right)^{c} \in \mathcal{A}$.

Above all, $\mathcal{A}$ is a field but not a $\sigma-$field necessarily, for instance let:
$A_{1} = \left\{ a_{1} \right\}, A_{2} = \left\{ a_{2} \right\}, A_{3} = \left\{ a_{3} \right\}, \ldots , \in \mathcal{A}$
then it is not necessary that: $\bigcup\limits^{\infty}_{n=1}A_{n} \in \mathcal{A}$.

---

Theorem 1.2

The intersection of (any) family of $\sigma-$fields over the same universal set $\Omega$ is a $\sigma-$field.

---

Proof. (Theorem 1.2)

1. $\Omega \in \mathcal{F}_{1}, \Omega \in \mathcal{F}_{2} \implies \Omega \in \mathcal{F}_{1} \cap \mathcal{F}_{2}$.
2. for $\forall A \in \mathcal{F}_{1} \cap \mathcal{F}_{2}$, we have $A \in \mathcal{F}_{1}$ and $A \in \mathcal{F}_{2}$, then $A^{c} \in \mathcal{F}_{1}$ and $A^{c} \in \mathcal{F}_{2}$, which implies $A^{c} \in \mathcal{F}_{1} \cap \mathcal{F}_{2}$.
3. for $\forall A_{1}, A_{2}, \ldots \in \mathcal{F}_{1} \cap \mathcal{F}_{2}$, similarly, $\bigcup\limits^{\infty}_{n=1}A_{n} \in \mathcal{F}_{1}$ and $\bigcup\limits^{\infty}_{n=1}A_{n} \in \mathcal{F}_{2}$, hence $\left( \bigcup\limits^{\infty}_{n=1}A_{n} \right) \in \mathcal{F}_{1} \cap \mathcal{F}_{2}$.