bzoj2127: happiness

Description

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

Input

第一行两个正整数n，m。接下来是六个矩阵第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

Output

输出一个整数，表示喜悦值总和的最大值

Sample Input

1 2
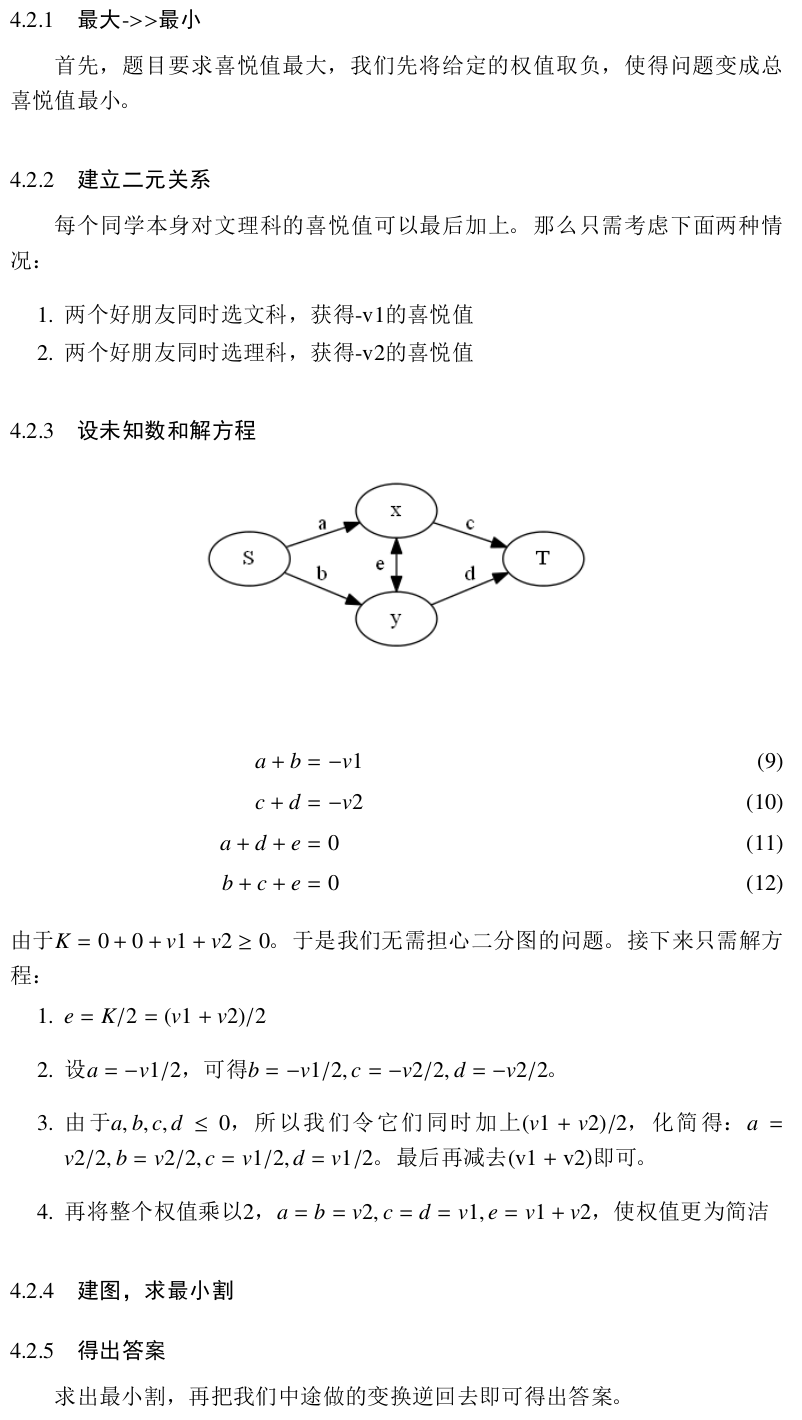
1 1
100 110
1
1000

Sample Output

1210
【样例说明】
两人都选理，则获得100+110+1000的喜悦值。
【数据规模】
对于100%以内的数据，n,m<=100 所有喜悦值均为小于等于5000的非负整数

 

题解：神奇的二元组建图

code：

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 10005
#define maxm 550000
#define inf 1061109567
using namespace std;
char ch;
bool ok;
void read(int &x){
    for (ok=0,ch=getchar();!isdigit(ch);ch=getchar()) if (ch=='-') ok=1;
    for (x=0;isdigit(ch);x=x*10+ch-'0',ch=getchar());
    if (ok) x=-x;
}
int n,m,a[105][105],b[105][105],c[105][105],d[105][105],ans;
struct flow{
    int s,t,tot,now[maxn],son[maxm],pre[maxm],val[maxm];
    int dis[maxn],head,tail,list[maxn];
    bool bo[maxn];
    void init(){s=0,t=n*m+1,tot=1,memset(now,0,sizeof(now));}
    void put(int a,int b,int c){pre[++tot]=now[a],now[a]=tot,son[tot]=b,val[tot]=c;}
    void add(int a,int b,int c){put(a,b,c),put(b,a,0);}
    bool bfs(){
        memset(bo,0,sizeof(bo));
        head=0,tail=1,list[1]=s,dis[s]=0,bo[s]=1;
        while (head<tail){
            int u=list[++head];
            for (int p=now[u],v=son[p];p;p=pre[p],v=son[p])
                if (val[p]&&!bo[v]) bo[v]=1,dis[v]=dis[u]+1,list[++tail]=v;
        }
        return bo[t];
    }
    int dfs(int u,int rest){
        if (u==t) return rest;
        int ans=0;
        for (int p=now[u],v=son[p];p&&rest;p=pre[p],v=son[p])
            if (val[p]&&dis[v]==dis[u]+1){
                int d=dfs(v,min(rest,val[p]));
                val[p]-=d,val[p^1]+=d,ans+=d,rest-=d;
            }
        if (!ans) dis[u]=-1;
        return ans;
    }
    int dinic(){
        int ans=0;
        while (bfs()) ans+=dfs(s,inf);
        return ans;
    }
}f;
inline int calc(int a,int b){return (a-1)*m+b;}
int main(){
    read(n),read(m),f.init();
    for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) read(a[i][j]);
    for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) read(b[i][j]);
    for (int i=1;i<=n;i++) for (int j=1;j<=m;j++){
        int u=calc(i,j);
        f.add(f.s,u,b[i][j]<<1),f.add(u,f.t,a[i][j]<<1);
        ans+=a[i][j]+b[i][j];
    }
    for (int i=1;i<n;i++) for (int j=1;j<=m;j++) read(c[i][j]);
    for (int i=1;i<n;i++) for (int j=1;j<=m;j++) read(d[i][j]);
    for (int i=1;i<n;i++) for (int j=1;j<=m;j++){
        int u=calc(i,j),v=calc(i+1,j);
        f.add(f.s,u,d[i][j]),f.add(f.s,v,d[i][j]);
        f.add(u,f.t,c[i][j]),f.add(v,f.t,c[i][j]);
        f.add(u,v,c[i][j]+d[i][j]),f.add(v,u,c[i][j]+d[i][j]);
        ans+=c[i][j]+d[i][j];
    }
    for (int i=1;i<=n;i++) for (int j=1;j<m;j++) read(c[i][j]);
    for (int i=1;i<=n;i++) for (int j=1;j<m;j++) read(d[i][j]);
    for (int i=1;i<=n;i++) for (int j=1;j<m;j++){
        int u=calc(i,j),v=calc(i,j+1);
        f.add(f.s,u,d[i][j]),f.add(f.s,v,d[i][j]);
        f.add(u,f.t,c[i][j]),f.add(v,f.t,c[i][j]);
        f.add(u,v,c[i][j]+d[i][j]),f.add(v,u,c[i][j]+d[i][j]);
        ans+=c[i][j]+d[i][j];
    }
    printf("%d\n",ans-(f.dinic()>>1));
    return 0;
}