仿射函数，线性函数以及泰勒公式还有泰勒估算...

 

1. 先说仿射函数和线性函数

线性函数平常非常常见：

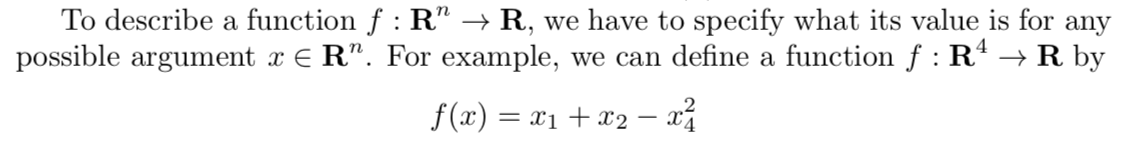
这里我们是将一个4维的向量最后投射到一个1维的值。不过这里注意，这个函数是经过原点的。

再看下仿射方程。

 

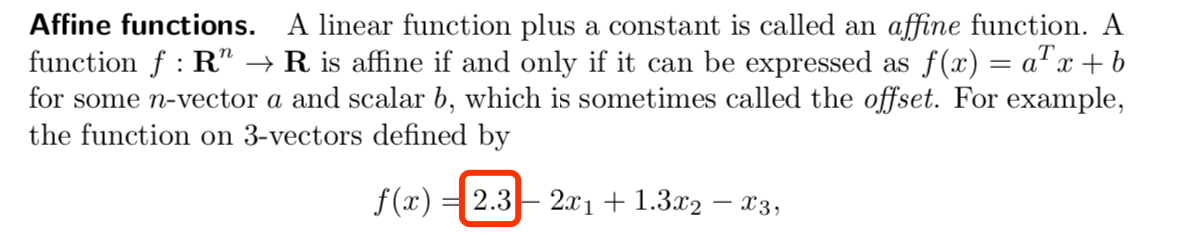
这里我们可以看下他们的区别

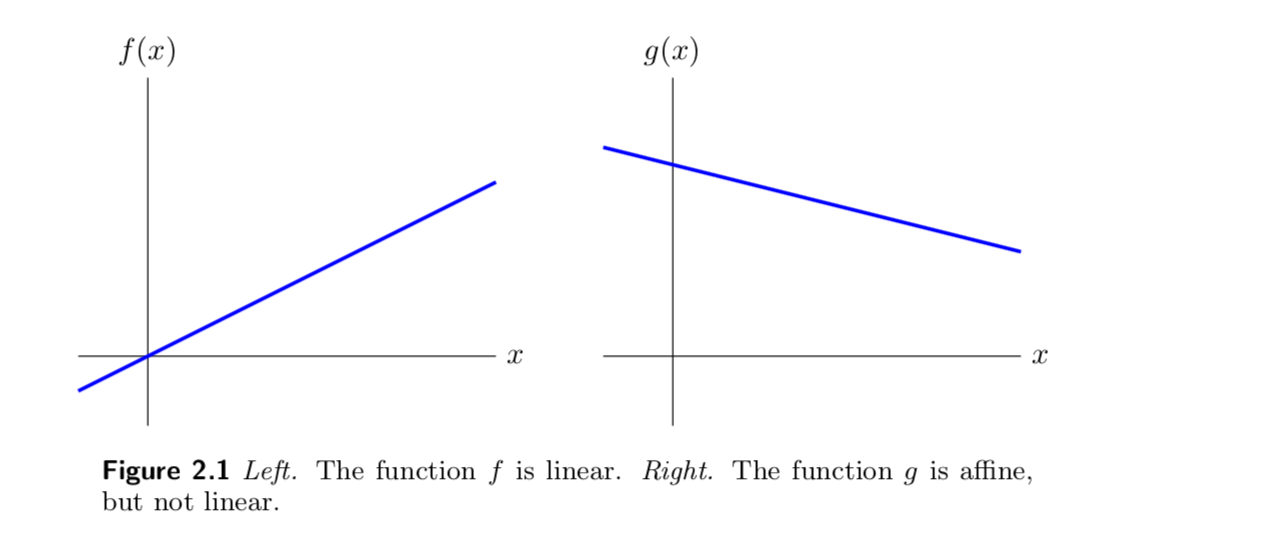
直观的区别就是会不会经过原点。

知乎上有大佬是这么解释“

仿射函数即由由1阶多项式构成的函数，一般形式为 f (x) = A x + b，这里，A 是一个 m×k 矩阵，x 是一个 k 向量,b是一个m向量，实际上反映了一种从 k 维到 m 维的空间映射关系。

设f是一个矢性（值）函数，若它可以表示为f(x1,x2,…,xn)=A1x1+A2x2+…+Anxn+b，其中Ai可以是标量，也可以是矩阵，则称f是仿射函数。
其中的特例是，标性（值）函数f(x)=ax+b，其中a、x、b都是标量。此时严格讲，只有b=0时，仿射函数才可以叫“线性函数”（“正比例”关系）。”

 

接着他们会有一些性质，我贴一下：

那我们也经常用这种办法来判断一个方程是不是仿射函数。

 

2. 泰勒估算

那先简单说下泰勒公式吧。

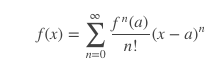
这个样子，就是说，我们可以把一个方程，写成多项式的形式。这个有其中一个好处，就是，我们去做一些估算。比如一个函数的值不能直接求到，我们能不能用这个方式来计算？

从函数的线性近似f(a+Δx)=f(a)+f′(a)Δxf(a+Δx)=f(a)+f′(a)Δx来估计函数值。

 

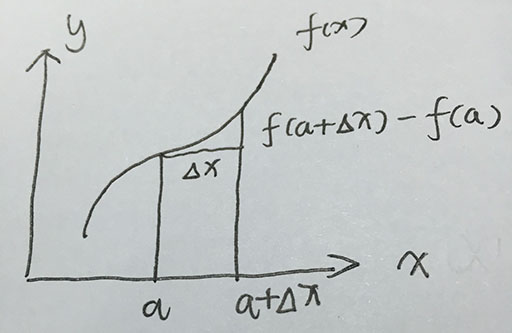
 这里，我们就可以尝试下泰勒的一级展开

当然了，这个倒后面，我们做优化的时候，用到的牛顿法，也有关系了，不过今天我不说。

后面看到那个R没有，我们叫余项，这里也就是说，n不可能无限对吧，我选了一个N，那一定和实际的有差距，这里也就是只是个估算。当然情况下，是有n阶导数了，没有的话，后面都是0，n也不是无穷的。

 

那我们看个比较简单的情况吧，针对我说的线性方程或者是仿射方程。

我们取一阶导数 这里 x是n-vector z是n-vector 

那这个估值，我们可以表示为

用梯度表示 更舒服一点。

这里有个例题，可以带着看下

我们用不同的点带进去看下

其实发现，离的越近，当然误差越小。

 

 

再安利一本数学书，非常推荐，vmls, 配套的语言是julia，有兴趣的来这里下载

 

 

 

 

链接：https://pan.baidu.com/s/1g6xSR0XbN7kh-FHetFpzKw 

提取码：gg36