【算法面试题】寻找二叉搜索树中两个节点的最近公共祖先节点（转）

【算法面试题】寻找二叉搜索树中两个节点的最近公共祖先节点

http://geeksforgeeks.org/?p=1029

给定了一个二叉搜索树中任意的两个节点的值，要你写一个c/c++程序，去找到这两个节点的最近公共祖先，你可以假定给定的值存在于二叉树的某个节点中。

函数声明：

int FindLowestCommonAncestor(node* root, int value1, int value)

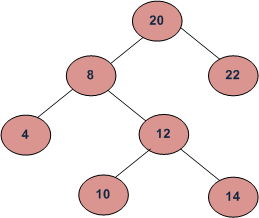
 输入: 4 和 14
 输出: 8
 （4和14的共同祖先有{8, 20}，其中8是最近的公共祖先节点）

算法：

基本思想是：给定二叉树中的两个节点n1, n2(假定n1<n2), 其最近的公共祖先节点的值n应该满足 n1<n<n2，所以我们可以前序遍历二叉搜索树，当发现一个节点的值在n1和n2之间时，则此节点为所求节点。如果节点的值大于n1和n2，则所求节点在当前节点的左子树；否则在右子树。（算法很简单，对于树的求解关键是用好先中后序遍历，再难也不过如此，呵呵）

#include <stdio.h>    
#include <stdlib.h>    
  
/* A binary tree node has data, pointer to left child   
   and a pointer to right child */   
  
struct node    
{    
    int data;    
    struct node* left;    
    struct node* right;    
};    
  
struct node* newNode(int );    
  
/* Function to find least comman ancestor of n1 and n2 */   
int leastCommanAncestor(struct node* root, int n1, int n2)    
{    
  /* If we have reached a leaf node then LCA doesn't exist   
     If root->data is equal to any of the inputs then input is   
     not valid. For example 20, 22 in the given figure */   
  
  if(root == NULL || root->data == n1 || root->data == n2)    
    return -1;     
  
  /* If any of the input nodes is child of the current node   
     we have reached the LCA. For example, in the above figure   
     if we want to calculate LCA of 12 and 14, recursion should   
     terminate when we reach 8*/   
  if((root->right != NULL) &&    
    (root->right->data == n1 || root->right->data == n2))    
    return root->data;    
  
  if((root->left != NULL) &&    
    (root->left->data == n1 || root->left->data == n2))    
    return root->data;        
  
  if(root->data > n1 && root->data < n2)    
    return root->data;    
  
  if(root->data > n1 && root->data > n2)    
    return leastCommanAncestor(root->left, n1, n2);    
  
  if(root->data < n1 && root->data < n2)    
    return leastCommanAncestor(root->right, n1, n2);    
}        
  
/* Helper function that allocates a new node with the   
   given data and NULL left and right pointers. */   
struct node* newNode(int data)    
{    
  struct node* node = (struct node*)    
                       malloc(sizeof(struct node));    
  node->data  = data;    
  node->left  = NULL;    
  node->right = NULL;    
  return(node);    
}    
  
/* Driver program to test mirror() */   
int main()    
{    
  struct node *root  = newNode(2);    
  root->left         = newNode(1);    
  root->ight        = newNode(4);    
  root->right->left  = newNode(3);    
  root->right->right = newNode(5);     
     
/* Constructed binary search tree is   
            2   
           / \   
          1   4   
             / \   
           3   5   
*/   
  
  printf("\n The Least Common Ancestor is \n");    
  printf("%d", leastCommanAncestor(root, 3, 5));    
  
  getchar();    
  return 0;    
}   

载自：http://blog.csdn.net/wangzhi0417/archive/2010/08/11/5803231.aspx