BloomFilter 与 Cuckoo Filter

BloomFilter 与 CuckooFilter

Bloom Filter

Bloom Filter是一种空间效率很高的随机数据结构，它的原理是，当一个元素被加入集合时，通过K个相互独立的Hash函数将这个元素映射成一个位阵列（Bit array）中的K个点，把它们置为1。检索时，我们只要看看这些点是不是都是1就（大约）知道集合中有没有它了；如果这些点有任何一个0，则被检索元素一定不在；如果都是1，则被检索元素很可能在。

Bloom Filter的这种高效是有一定代价的，在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，并不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

假设要你写一个网络爬虫程序（web crawler）。由于网络间的链接错综复杂，爬虫在网络间爬行很可能会形成“环”。为了避免形成“环”，就需要知道爬虫程序已经访问过那些URL。给一个URL，怎样知道爬虫程序是否已经访问过呢？稍微想想，就会有如下几种方案：

将访问过的URL保存到数据库。
用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。
URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。
Bit-Map方法。建立一个BitSet，将每个URL经过一个哈希函数映射到某一位。

其中，方法1~3都是将访问过的URL完整保存，方法4则只标记URL的一个映射位。以上方法在数据量较小的情况下都能完美解决问题，但是当数据量变得非常庞大时问题就来了：

方法1：数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了？

方法2：太消耗内存。随着URL的增多，占用的内存会越来越多。就算只有1亿个URL，每个URL只算50个字符，就需要5GB内存。

方法3：由于字符串经过MD5处理后的信息摘要长度只有128Bit，SHA-1处理后也只有160Bit，因此方法3比方法2节省了好几倍的内存。

方法4：消耗内存是相对较少的，但缺点是单一哈希函数发生冲突的概率太高。还记得数据结构课上学过的Hash表冲突的各种解决方法么？若要降低冲突发生的概率到1%，就要将BitSet的长度设置为URL个数的100倍。Bloom Filter 与单哈希函数Bit-Map不同之处在于：Bloom Filter使用了k个哈希函数，每个字符串跟k个bit对应。从而降低了冲突的概率。

创建一个m位BitSet，先将所有位初始化为0，然后选择k个不同的哈希函数。第 i 个哈希函数对字符串str哈希的结果记为H_i(str)，并且满足：

0 <= H_i(str) < m 　　　　（1<=i<=k）

(1) 将字符串 str 映射到BitSet中的过程：分别计算H₁(str)，H₂(str)，…，H_k(str)，然后在BitSet中将对应的位置1。

(2) 检查字符串str是否被BitSet记录过的过程：分别计算H₁(str)，H₂(str)，…，H_k(str)，然后在BitSet中对应的位检查是否为1。若其中任何一位不为1则可以判定str一定没有被记录过。若全部位都是1，则认为字符串str存在。注意：这里也可能存在误判，因为有可能该字符串的所有位都刚好是被其他字符串所对应，这种将该字符串划分错的情况称为false positive 。

(3) 删除字符串过程，字符串加入了就被不能删除了，因为删除会影响到其他字符串。

实在需要删除字符串的可以使用Counting Bloom Filter (CBF)，这是一种基本Bloom Filter的变体，CBF将基本Bloom Filter每一个Bit改为一个计数器，这样就可以实现删除字符串的功能了。

Bloom Filter 参数选择

问题：m（bit-map位数）, n（待处理的字符串个数）, k（哈希函数个数）值，我们该如何取值呢？

当hash函数个数 k = (ln2) * (m/n) 时错误率最小。

在错误率不大于e的情况下，则m >= n*log₂(1/e)*log₂e 。

这里直接给出了结论，如果对上述公式推导过程感兴趣，可以参考这里。

举个例子我们假设错误率为0.001，则此时m应大概是n的14倍。这样k大概是4个。

一个实现

https://github.com/chenny7/bloom

D-left Counting Bloom Filter

传统的Bloom Filter不能作删除操作，我们可以使用CBF（counting bloom filter）来支持删除功能。

Standard CBF（SCBF）就是将BF的bit扩展成counter，比如每个counter占4个bits，插入key时自增，删除key时自减，但SCBF的空间就会比BF增加4倍。

D-left CBF 是为了提高CBF的空间效率提出的，其数据结构如下：

将一个哈希表分成几个不相交的子表（subtable），每个子表里都有数量相同的桶（bucket），每个桶里都有一定数量的单元（cell，单元包括特征值和计数值），每个单元都是固定的位数组成，用来保存元素的特征值（fingerprint），只有一个哈希函数，该哈希函数可以生成和子表数量相同的桶地址和一个特征值

用golang描述：

const bucketHeight = 8

type fingerprint uint16

type bucket struct {
    entries [bucketHeight]fingerprint
    count   uint8
}

type table []bucket

/*
Dlcbf is a struct representing a d-left Counting Bloom Filter
*/
type Dlcbf struct {
    tables     []table
    numTables  uint
    numBuckets uint
}

比如插入一个key的流程具体为：

假设有 d 个子表，元素为 x，哈希函数为 f，计算 f(x)，生成桶地址 addr0, addr1, ..., addr(d-1)，并得到特征值 p；
我们检查子表 i 中地址为 addri 的桶中的所有单元（i = 0，1，...，d-1）；
如果某个cell中的特征值和 p 相等，那么元素 x 就在该哈希表中；
若没有找到这样的cell，那么需要找到存储特征值最少的桶（在上面生成的桶地址中找），然后将该特征值 p 随机放入该桶的一个空单元中，该单元的计数值变为1，这考虑了装载平衡。

一个实现：

https://github.com/chenny7/dlCBF

Cuckoo 布谷鸟哈希

前面提到，Bloom Filter 可能存在误报，并且无法删除元素，而Cuckoo哈希就是解决这两个问题的。

Cuckoo的哈希函数是成对的（具体的实现可以根据需求设计），每一个元素都是两个，分别映射到两个位置，一个是记录的位置，另一个是备用位置，这个备用位置是处理碰撞时用的。

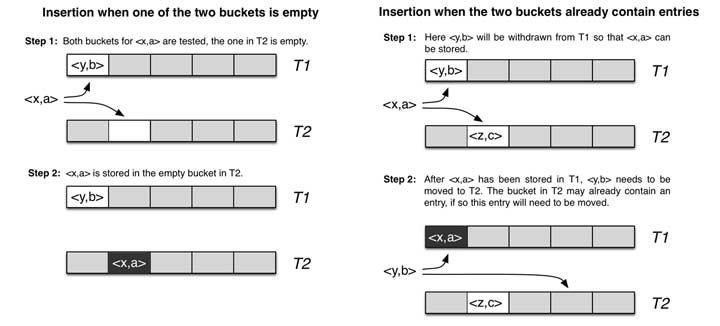
如下图，使用hashA 和hashB 计算对应key x的位置a和b ：

当两个哈希位置有一个为空时，则插入该空位置；
当两个哈希位置均不为空时，随机选择两者之一的位置上key y 踢出，并计算踢出的key y在另一个哈希值对应的位置，若为空直接插入，不为空踢出原元素插入，再对被踢出的元素重新计算，重复该过程，直到有空位置为止。

比如待存储的key=x，首先计算其指纹、以及两个hash函数的结果（对应存储位置）

fp = fingerprint(x)
p1 = hash1(x) % len
p2 = hash2(x) % len

如果p1、p2两个位置都已满，那么我们需要随机选择其中一个未知的元素进行踢出，并计算其另一个对位，

但由于cuckoo filter存储的是指纹fp，而非原始的x值，那么要如何计算其另一个位置呢？

cuckoo filter巧妙的设计另一个hash函数，使得可以根据 p1 和 fp 直接计算出 p2（或者根据p2 和 fp 直接计算出 p1），而不需要完整的 x 元素。

fp = fingerprint(x)
p1 = hash(x)
p2 = p1 ^ hash(fp)  // 异或

同样的

p1 = p2 ^ hash(fp)

所以我们根本不需要知道当前的位置是 p1 还是 p2，只需要将当前的位置和 hash(fp) 进行异或计算就可以得到对偶位置。而且只需要确保 hash(fp) != 0 就可以确保 p1 != p2，如此就不会出现自己踢自己导致死循环的问题。

cuckoo filter 数据结构(go描述)，简单起见，我们假定指纹占用一个字节（指纹范围 (0-255] ），每个位置有 4 个座位：

type bucket [4]byte  // 一个桶，4个座位
type cuckoo_filter struct {
  buckets [size]bucket // 一维数组
  nums int  // 容纳的元素的个数
  kick_max  // 最大挤兑次数
}

插入算法，需要考虑到最坏的情况，那就是挤兑循环。所以需要设置一个最大的挤兑上限，当超过挤兑上限时，可以进行扩容（rehash）。

def insert(x):
  fp = fingerprint(x)
  p1 = hash(x)
  p2 = p1 ^ hash(fp)
  // 尝试加入第一个位置
  if !buckets[p1].full():
    buckets[p1].add(fp)
    nums++
    return true
  // 尝试加入第二个位置
  if !buckets[p2].full():
    buckets[p2].add(fp)
    nums++
    return true
  // 随机挤兑一个位置
  p = rand(p1, p2)
  c = 0
  while c < kick_max:
    // 挤兑
    old_fp = buckets[p].replace_with(fp)
    fp = old_fp
    // 计算对偶位置
    p = p ^ hash(fp)
    // 尝试加入对偶位置
    if !buckets[p].full():
      buckets[p].add(fp)
      nums++
      return true
    c++
  return false

查找算法

def contains(x):
  fp = fingerprint(x)
  p1 = hash(x)
  p2 = p1 ^ hash(fp)
  return buckets[p1].contains(fp) || buckets[p2].contains(fp)

删除算法

def delete(x):
  fp = fingerprint(x)
  p1 = hash(x)
  p2 = p1 ^ hash(fp)
  ok = buckets[p1].delete(fp) || buckets[p2].delete(fp)
  if ok:
    nums--
  return ok

考虑一下，如果cuckoo filter对同一个元素进行多次连续的插入会怎样？

根据上面的逻辑，毫无疑问，这个元素的指纹会霸占两个位置上的所有座位 —— 8个座位(2个位置各4个座位)。这 8 个座位上的值都是一样的，都是这个元素的指纹。如果继续插入，则会立即出现挤兑循环。从 p1 槽挤向 p2 槽，又从 p2 槽挤向 p1 槽。

也许你会想到，能不能在插入之前做一次检查，询问一下过滤器中是否已经存在这个元素了？这样确实可以解决问题，插入同样的元素也不会出现挤兑循环了。但是删除的时候会出现一定概率的误删。因为不同的元素被 hash 到同一个位置的可能性还是很大的，而且指纹只有一个字节，256 种可能，同一个位置出现相同的指纹可能性也很大。如果两个元素的 hash 位置相同，指纹相同，那么这个插入检查会认为它们是相等的。

可见，如果要让cuckoo filter支持删除操作，就必须允许重复插入，但必须确保同一个元素插入次数不超过kb，这里k指hash函数个数，b指每个位置上的座位数。

如果同一个元素插入次数达到 kb+1 次，会引起循环挤兑，即使扩容也无法解决。确保一个元素不被插入指定的次数那几乎是不可能做到的，除非我们再维护一个外部的字典来记录每个元素的插入次数，但这个外部字典的存储空间怎么办呢？

当然如果不支持删除操作，那么布谷鸟过滤器单纯从空间效率上来说还是有一定的可比性的。

此外，

Cockoo hashing 有两种变形：一种通过增加哈希函数进一步提高空间利用率；另一种是增加哈希表，每个哈希函数对应一个哈希表，每次选择多个张表中空余位置进行放置，三个哈希表可以达到80% 的空间利用率。

Cockoo hashing 的过程可能因为反复踢出无限循环下去，这时候就需要进行一次循环踢出的限制，超过限制则认为需要添加新的哈希函数。

Cuckoo Filter 参数选择

cuckoo空间大小 = 桶大小(b) * 桶个数(m) * fingerprint 位数(f) / 负载系数(a)；

a = 最大key数量(n) / (b * m)

b大小的选择，考虑两点

b越大，load factor (a)越高。使用2个hash函数时（每个key有2个桶下标），如果b=1（每个桶只有1个slot），a=50%（退化成map表），b到达2、4、8时，a分别为84%、95%、98%；
要保持false positive概率一定，更大的桶就需要更长的fingerprint，这是因为桶越大，需要查找比对的fingerprint越多 (2*b)，碰撞概率也越大，因此需要的 fingerprint位数f 也愈大。

根据原论文的模拟实验，当 false positive > 0.002时 b=2最佳，当 0.00001 < false positive <= 0.002时b=4最佳。

假设：