图
1.学习总结
1.1图的思维导图

1.2 图结构学习体会
(一)图的遍历有两种遍历方式:深度优先遍历(depth-first search)和广度优先遍历(breadth-first search)。
1.深度优先遍历
基本思路:首先从图中某个顶点V0出发,然后依次从V0相邻的顶点出发深度优先遍历,直至图中所有与V0路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。可以看出深度优先遍历是一个递归的过程。
如下图中的一个无向图:
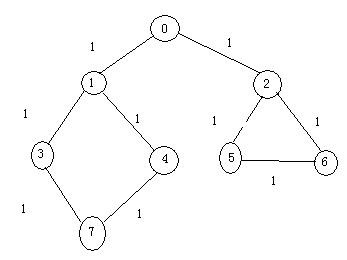
其深度优先遍历得到的序列为:
0->1->3->7->4->2->5->6
2.广度优先遍历
基本思路:首先,从图的某个顶点V0之后,访问了V0之后,依次访问与V0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。也是递归的问题。
如上面图中
其广度优先遍历得到的序列:
0->1->2->3->4->2->5->6->7
3.深度优先遍历和广度优先遍历区别
- 广度优先搜索与深度优先搜索的时间复杂度相同,只是遍历顺序不同。
(二)Prim和Kruscal算法
Kruscal算法:
1.问题描述:设G=(V,E)是无向连通带权图,如果G的一个子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。生成树的各边权的总和称为该生成树的耗费,求在G的所有生成树中耗费最小的最小生成树。
2.算法思想:
(1)将代价树中权值非0的所有的边进行小顶堆排序,依次存入到road[]数组中,然后将road[]进行倒置,注意在进行排序时,按照road[i]的权值进行排序,然后记录这条边的起始顶点也要相对应。
(2)从最小边开始扫描各边,并检测当前所选边的加入是否会构成回路,如果不会构成回路,则将该边并入到最小生成树中。
(3)不断重复步骤2,直到所有的边都检测完为止。
其中判断当前检测边的加入是否会使原来生成树构成回路的算法思想是:
(1)采用树的双亲存储结构,即数组v[i]的值表示编号为i的顶点的父结点编号。并将数组v[]初始化为v[i]=i;
(2)若当前要并入的边起点为a,终点为b,需要判断起点a是否被修改过,即a!=v[a],若已被修改过,就要修改终点v[b]的值,使v[b]=a,即结点b的父结点为a。
(3)若当前检测的边结点起点为a,终点为b,则判断该边是否能被加入的方法是:分别访问a,b的根结点(a,b的父结点有可能还有父结点),若a,b的根结点相同,则不可以并入,否则可以将该边并入。
Prim算法:
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={s},v=V−u;
- 在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息
三,Dijkstra算法:
1.算法描述
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中
(四)拓扑排序算法:
1.定义:是将一个有向无环图G的所有的顶点排成一个线性序列,使得有向图中的任意的顶点u 和 v 构成的弧<u, v>属于该图的边
集,并且使得 u 始终是出现在 v 的前面。通常这样的序列称为是拓扑序列。
2注意:
只有有向无环图才可以进行拓扑排序
3、算法思想:
1).找到有向无环图中没有前驱的节点(或者说是入度为0的节点)输入;
2).然后从图中将此节点删除并且删除以该节点为尾的弧;
2.PTA实验作业
2.1 题目1:图着色问题
图着色问题是一个著名的NP完全问题。给定无向图,,问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:
输入在第一行给出3个整数V(0)、E(≥)和K(0),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
2.2 设计思路
伪代码:
for (int i = 0; i < m; i++) {
set<int> s;
for (int j = 0; j < v; j++) {
设置一个循环读入无向图的数
}
if (s.size() != k) {
令flag等于false;
} else {
memset(vis, false, sizeof(vis));
flag = true;
for (int j = 0; j < v; j++) {
//判断是否成立
if (flag == false) {
结束循环
}
}
}
2.3 代码截图:

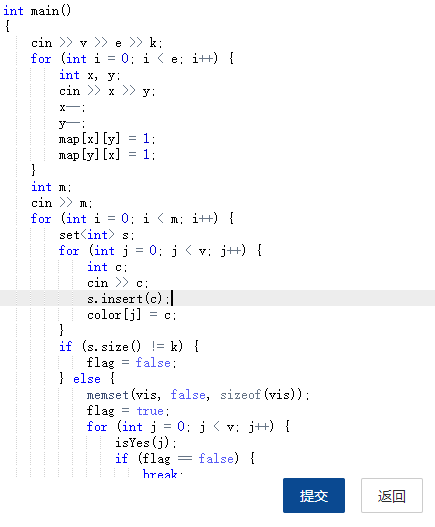
2.4 PTA提交列表说明:
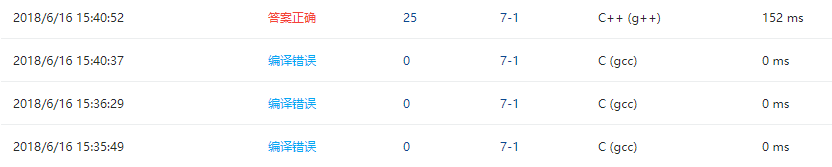
最开始编译的时候调用了函数,用c语言运行一直编译错误。后来改过几次才意识到了编译器的问题,所以改正了过来。
题目2:公路村村通;
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤)和候选道路数目M(≤);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−,表示需要建设更多公路。
2. 设计思路:
解题思路:1、这道题一开始走偏了想直接同floyd算法求出最短路径然后相加了
最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。
最短路径是从一点出发,到达目的地的路径最小。
2、理清楚了最小生成树与最短路径之间的区别以后就很容易想到用最小生成树算法了,这里选用的是Prim算法
3 代码截图:

4 PTA提交列表说明:

题目3:畅通工程之最低成本建设问题
某地区经过对城镇交通状况的调查,得到现有城镇间快速道路的统计数据,并提出“畅通工程”的目标:使整个地区任何两个城镇间都可以实现快速交通(但不一定有直接的快速道路相连,只要互相间接通过快速路可达即可)。现得到城镇道路统计表,表中列出了有可能建设成快速路的若干条道路的成本,求畅通工程需要的最低成本。
输入格式:
输入的第一行给出城镇数目N (1)和候选道路数目M≤3N;随后的M行,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号(从1编号到N)以及该道路改建的预算成本。
输出格式:
输出畅通工程需要的最低成本。如果输入数据不足以保证畅通,则输出“Impossible”
2. 伪代码:
定义
for(int i=0;i<N;i++)
{//初始化 }
//对edge数组的1---P号边进行排序
qsort(edge, P, sizeof(edge[0]), cmp);
for(int i=0;i<P;i++)
{//对前面排序后,这里每次都要选择最小,这也是贪心的思想
//S和E代表了一条通路
if(Find(S)!= Find(E)){
w += edge[i].L;
将两个结点连接;
cnt++;
if(cnt >= N-1)
break; }}
3 代码截图:

4 PTA提交列表说明:
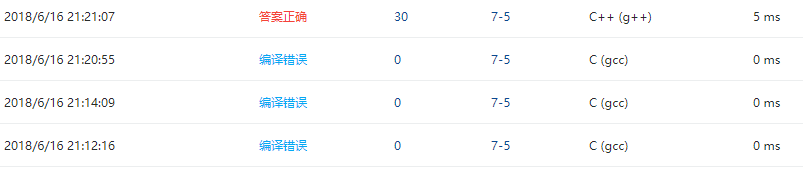
最开始没有使最根结点为负的操作(num = far[rS] + far[rE];)然后出现的编译错误。
后来改正了错误之后还是编译错误,又是编译器的错误。换了c++之后才答案正确。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:134
4. 阅读代码:
题目:搜索树判断:
对于二叉搜索树,我们规定任一结点的左子树仅包含严格小于该结点的键值,而其右子树包含大于或等于该结点的键值。如果我们交换每个节点的左子树和右子树,得到的树叫做镜像二叉搜索树。
现在我们给出一个整数键值序列,请编写程序判断该序列是否为某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列,如果是,则输出对应二叉树的后序遍历序列。
解题思路:1.首先是判断是否是二叉搜索树,给出先序遍历,因而先序的第一个数字是根结点,
找到第一个大于等于根节点的数字,从这个数字开始为右子树,若右子树中有小于根结点的数
那么它不是二叉搜索树; 镜像结点判断条件相反即可
2、倘若是二叉搜索树则一边递归一边生成二叉树,最后返回根节点
3、对二叉搜索树进行后序遍历
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h> 4
5 typedef struct TNode *tree;
6 struct TNode
{ 8 int data;
9 tree lchild;
10 tree rchild; 11 };
12 int flag = 0; //控制最后一个输出后面没有空格
13 int flag1 ; //如果不是二叉搜索树返回1
14 int flag2 ; //如果不是二叉镜像搜索树返回1
16 void Print( tree t);
17 tree Find ( int pre[],int len);
18 tree FindMirror( int pre[],int len);
20 int main() {
22 int len;
23 int pre[1005];
24 int i;
25 tree t,tm;
27 scanf("%d",&len);
28 for( i=0; i<len; i++) {
30 scanf("%d",&pre[i]);
31 }
33 t = Find( pre,len);
34 tm = FindMirror( pre,len );
35 if( t && !flag1)
36 {
37 //树不为空并且是二叉搜索树
38 printf("YES\n");
39 Print( t );
40 printf("\n");
41 }
42 else if( tm && !flag2)
43 {
44 //树不为空并且是二叉镜像搜索树
45 printf("YES\n");
46 Print( tm );
47 printf("\n");
48 }
49 else printf("NO\n");
50
51 return 0;
52 }
53
54
55 tree Find ( int pre[],int len)
56 {
57 int i,j;
58
59 if( !len ) return NULL;
60 tree temp = (tree) malloc( sizeof( struct TNode));
61 temp->data = *pre;
62
63 for( i=1; i<len; i++)
64 {
65 if( pre[i] >= temp->data)
66 //寻找右子树
67 break;
68 }
69 for( j=i; j<len; j++)
70 {
71 if( pre[j] < temp->data)
72 {
73 //右子树中有小于根结点的值,不是二叉搜索树
74 flag1 = 1;
75 return NULL;
76 }
77 }
78 temp->lchild = Find( pre+1, i-1);
79 temp->rchild = Find( pre+i, len-i);
80 return temp;
81 }
82 tree FindMirror( int pre[],int len)
83 {
84 //镜像树,左子树大于根大于右子树
85 int i,j;
86
87 if( !len ) return NULL;
88 tree temp = (tree) malloc( sizeof( struct TNode));
89 temp->data = *pre;
90
91 for( i=1; i<len; i++)
92 {
93 if( pre[i] < temp->data)
94 //寻找右子树
95 break;
96 }
97 for( j=i; j<len; j++)
98 {
99 if( pre[j] >= temp->data)
100 {
101 //右子树中有大于等于根结点的值,不是二叉搜索树
102 flag2 = 1;
103 return NULL;
104 }
105 }
106 temp->lchild = FindMirror( pre+1, i-1);
107 temp->rchild = FindMirror( pre+i, len-i);
108 return temp;
109 }
110
111 void Print( tree t)
112 {
113
114 if( t )
115 {
116 //后序遍历
117 Print(t->lchild);
118 Print(t->rchild);
119 if( !flag ) flag = 1;
120 else printf(" ");
121 printf("%d",t->data);
122 }
123 }


