【数论算法理论与实现】
【题目太正式了我还怎么写ヾ|≧_≦|〃】
【很简要】
【参考文献:《算法导论》、白书、gty课件,LH课件】
[2016-08-13 ]
[2017-02-14 update (Valentine's Day就写这玩意?!]
1.基础
【除法定理】:对于任何整数a和正整数n,存在唯一整数q和r,满足0<=r<n且a=qn+r
WARN:C++中貌似不完全遵守这个东西,n认为是|n|,并且a为负时r可以为负
这是算法导论上的说法,有很多资料上并不遵守r是正整数
有用的式子: a%b=a-a/b*b
2.最大公约数
几条性质:gcd(a,b)=gcd(|a|,|b|)
gcd(a,0)=|a|
gcd(a,ka)=|a|
gcd(a,b)=gcd(b,a mod b) --->Euclid算法
gcd(na,nb)=n*gcd(a,b) ---->Stein算法
当k与b互为质数,gcd(ka,b)=gcd(a,b) ---->Stein算法
gcd(a,b)是a与b的线性组合集{ax+by: x,y belong Z}中最小的元素
【Euclid算法、扩展欧几里德算法】
int gcd(int a,int b){return b==0?a:gcd(b,a%b);} int lcm(int a,int b){return a/gcd(a,b)*b;} void exgcd(int a,int b,int &d,int &x,int &y){ if(!b) d=a,x=1,y=0; else exgcd(b,a%b,d,y,x),y-=(a/b)*x; }
扩展欧几里得算法:
求解 ax+by=gcd(a,b) 的解 (x0,y0) ,满足|x0|+|y0|最小,可能为负
过程:
边界 b==0时 ,d=a,x=1,y=0式子成立;
知道b*x1+a%b*y1=gcd(a,b)的(x1,y1) , 求ax+by=gcd(a,b)的(x,y)
用a%b=a-⌊a/b⌋*b来替换
x1*b + y1*a - y1*⌊a/b⌋*b = gcd(a,b)
y1*a + (x1-y1*⌊a/b⌋)*b = gcd(a,b)待定系数法
x=y1, y=x1-y1*⌊a/b⌋;
求解不定方程:
ax+by=c --> 如果 gcd(a,b) | c 同乘c/gcd(a,b)
直线上的整点
任意解: (x0+kb',y0-ka') , a'=a/gcd(a,b)=lcm(a,b)/b 想象坐标系,加上lcm(a,b)后还是在直线上的整点
【Stein算法】(更相减损术改)
原文:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。
改进:利用上面那个性质
优势:不用除法 高精/位运算都很方便
int stein(int a,int b){
if(a==0||b==0) return a==0?b:a;
if(a&1==0&&b&1==0) return 2*stein(a>>1,b>>1);
if(a&1==0) return stein(a>>1,b);
if(b&1==0) return stein(a,b>>1);
return stein(min(a,b),abs(a-b));
}
3.唯一分解定理
一个比较好的分解质因子的写法,用了线性筛,保存lp[i]为数字i的最小质因子
唯一智障的缺点是必须先筛到n,所以n大时还是正常点筛sqrt(n)然后一个个质数试吧

bool notp[N]; int p[N],lp[N],lpnum[N]; void sieve(int n){ for(int i=2;i<=n;i++){ if(!notp[i]) p[++p[0]]=i,lp[i]=i,lpnum[i]=p[0]; for(int j=1;j<=p[0]&&i*p[j]<=n;j++){ notp[i*p[j]]=1;lp[i*p[j]]=p[j];lpnum[i*p[j]]=j; if(i%p[j]==0) break; } } } int e[N]; void fac(int x,int e[]){ while(x!=1){ int j=lpnum[x]; while(x%p[j]==0) x/=p[j],e[j]++; printf("e %d %d\n",p[j],e[j]); } } void invfac(int x,int e[]){ while(x!=1){ int j=lpnum[x]; while(x%p[j]==0) x/=p[j],e[j]--; } }
4.Prime 1
【一个整数a>1只能被平凡约数1和自身所整除】
【判质数】:
(1)朴素

bool isP(int n){ if(n<=1) return false; int m=floor(sqrt(n)+0.5); for(int i=2;i<=m;i++) if(n%i==0) return false; return true; }
(2)Miller-Rabin(见下面)
【筛质数】:
(1)【Eratosthenes筛法】 复杂度O(nlogn)
[每一个质数筛掉它的倍数 一定有一个小于根号n的质因子]

const int N=1e9; bool vis[N]; void era(int n){ int m=sqrt(n)+1; for(int i=2;i<=m;i++) if(!vis[i]) for(int j=i*i;j<=n;j+=i) vis[j]=true; }
(2)【欧拉筛法/线性筛】 复杂度O(n)
[对于任意一个合数,我们可以拆成最小质数*某个数字的形式。
我们枚举『某个数字』i(区分与埃氏筛法的枚举质因数),然后再从第一个质数开始枚举,进行筛选。
为了保证每个合数只被最小质因数筛选,当我们枚举的质数可以整除『某个数字』时,如果再往大里枚举,枚举的质数就不可能是最小质数了(因为i里都有这个质数了,再往下枚举比这个质数还大怎么可能是最小)]

bool flag[N]; int prime[N]; //O(n) int euler(int n){ int cntprime=0; for(int i=2;i<=n;i++){ if(!flag[i]) prime[++cntprime]=i; for(int j=1;j<=cntprime&&prime[j]*i<=n;j++){ flag[prime[j]*i]=true; if(i%prime[j]==0) break; } } return cntprime; }
5.同余、模
+ - * 在%n时的性质略
完全剩余系Zn:对于一个正整数n,一个整数集模n所得的余数域。[0,n-1]
[a]n={a+kn : k belong z} 包含a的模n等价类
Zn={[a]n : 0<=a<=n-1}={0,1,2,...,n-1}
------------------------------------------
逆元:ax≡1(mod n) x->a关于模n的逆元(inverse) gcd(a,n)=1时唯一解,否则无解
同余系除法:乘以逆元
【解模线性方程】
方法1:不定方程角度
ax≡b(mod n) ax-ny=b b | d=gcd(a,n)则有解,用exgcd求ax+ny=d的解然后同乘b/d就行了
任意解+k*n/d,逆元的时候d=1
根据方法2,现在也是mod n'意义下,他的解的个数在mod n意义下也是d个(这种情况下负数应该不算吧.....)
方法2:逆元角度
方程同除gcd(a,b) , a'x≡b'(mod n') ,x≡b'a'-1(mod n')
这样得到了mod n'(n'=n/d)意义下的解,mod n意义下有d个解 p+k*n',0<=k<=d-1
【exgcd求逆元】
或欧拉定理
int inv(int a,int n){ int d,x,y; exgcd(a,n,d,x,y); return d==1?(x+n)%n:-1; }
6.Prime 2
【互质数】:两个整数a,b满足gcd(a,b)=1
【约数的个数】:对于n=p1^a1*p2^a2*...*pk^ak, 约数的个数=∏(ai+1) : i=1..k= (a1+1)(a2+1)...(ak+1)
【欧拉函数】:对于n=p1^a1*p2^a2*...*pk^ak, φ(n)=n(1-1/p1)(1-1/p2)...(1-1/pk) phi(1)=1
-------------缩系Zn* :小于n且与n互质 |Zn*|=φ(n)
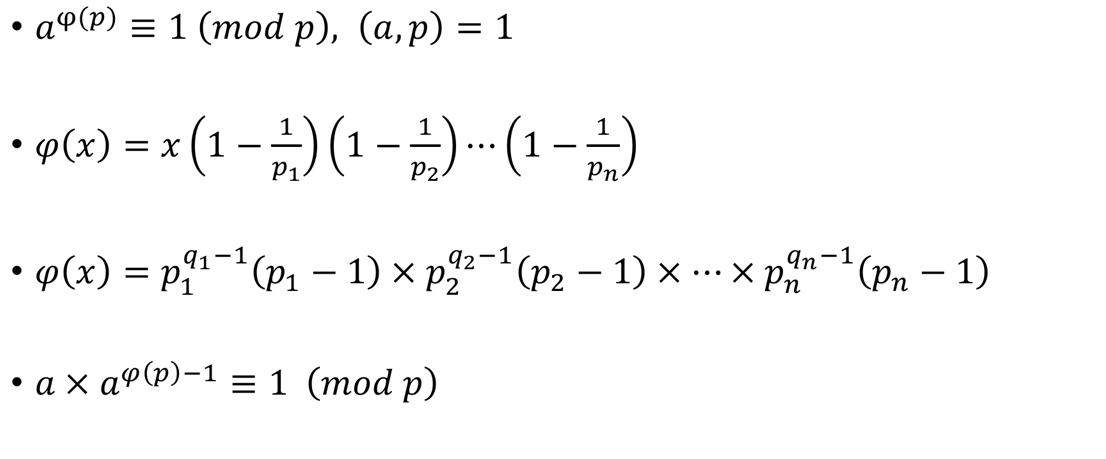
【素数定理】:pi(n) = n/ln n (略大)
【欧拉定理】: a^φ(n) ≡ 1(mod n)
【费马定理】:assume p is prime,且gcd(a,p)=1,则 a^(p-1) ===1(mod n)
求逆元:
1.exgcd 上面
2.aphi(p)-1 mod p
3.线性递推所有数的逆元:
http://blog.miskcoo.com/2014/09/linear-find-all-invert
这个做法实际上是这样的,首先 1−1≡1(mod p)
然后我们设 p=k⋅i+r, r<i, 1<i<p
再将这个式子放到mod p意义下就会得到
两边同时乘上 i−1⋅r−1 再移项将k代入就会得到
inv[i]= inv[p mod i] *(-p/i) (mod p)

void getInv(int n){ inv[1]=1; for(int i=1;i<=n;i++){ if(i!=1) inv[i]=-(ll)P/i*inv[P%i]%P; if(inv[i]<0) inv[i]+=P; } }
【计算欧拉函数】:
(1) 单个 根号n求唯一分解算公式就行了
(2)多个直接上线性筛 考虑公式
int phi(int n){ int m=sqrt(n+0.5); int ans=n; for(int i=2;i<=m;i++) if(n%i==0){ ans=ans/i*(i-1); while(n%i==0) n/=i; } if(n>1) ans=ans/n*(n-1); //n self is prime return ans; }
线性筛
void sieve(){ phi[1]=1; for(int i=2;i<=n;i++){ if(!vis[i]){ p[++m]=i; phi[i]=i-1; } for(int j=1;j<=m&&i*p[j]<=n;j++){ vis[i*p[j]]=1; if(i%p[j]==0){ phi[i*p[j]]=phi[i]*p[j]; break; } phi[i*p[j]]=phi[i]*(p[j]-1); } } for(int i=1;i<=n;i++) s[i]=s[i-1]+phi[i]; }
【Miller-Rabin】质数检测(很神的东西)
复杂度log级O(slogn)
链接 :素数算法时间测试 Miller-Rabin快速素性检测


