算法与数据结构 (三) 二叉树的简单应用 二叉查找树,二叉堆排序
一 二叉查找树
二叉查找树又叫二叉排序树,是为了解决查找的效率问题。正常情况下查找一个元素,需要O(n)的代价,但是如果查找元素有顺序,有序数组:可以用二分查找降低到 lgn 代价,但是有序链表的代价还是O(n) 因为,链表不支持随机访问,定位不到中间元素,从而不可以一次就排除掉一半元素。此时二叉查找树的出现,完美解决了这个问题,左边的全比根小,右边的全比根大。所以理想状态下也是一次淘汰一半元素(当然不理想,所以出现了红黑树和平衡二叉排序树),一次淘汰一半(实际淘汰不了)和二分查找思路不谋而合。树的简单实现(包括查找,插入,删除算法):
package tree.one;
import tree.MyTree;
import java.util.ArrayDeque;
import java.util.Queue;
public class FindTree {
private FindTree left;
private FindTree right;
private int val;
FindTree() {
}
FindTree(int val) {
this.val = val;
}
//插入一个节点
public static void insert(FindTree tree, int n) {
if (tree.left == null && n < tree.val) {
tree.left = new FindTree(n);
return;
}
if (tree.right == null && n > tree.val) {
tree.right = new FindTree(n);
return;
}
if (n < tree.val) {
insert(tree.left, n);
} else {
insert(tree.right, n);
}
}
//查找节点
public static boolean findNode(FindTree tree,int n){
if(tree.val==n)
return true;
while(tree!=null){
if(tree.val<n)
tree = tree.right;
else if(tree.val>n)
tree = tree.left;
else
return true;
}
return false;
}
//中序遍历
public static void showTree(FindTree tree) {
if (tree == null)
return;
showTree(tree.left);
System.out.print(tree.val + " ");
showTree(tree.right);
}
// 层次遍历
public static void showTree1(FindTree tree){
if (tree == null)
return;
Queue<FindTree> queue = new ArrayDeque<>();
FindTree now = null;
queue.offer(tree);
while (!queue.isEmpty()) {
now = queue.poll();
System.out.print(now.val + " ");
if (now.left != null)
queue.offer(now.left);
if (now.right != null)
queue.offer(now.right);
}
}
//删除节点
public static void deleteNode(FindTree tree ,int n){
if(!findNode(tree, n)){
System.out.println("删除的元素不存在");
return;
}
FindTree now = null;
while(true){
if(tree.left!=null) {
if (tree.left.val == n) {
tree.left = nextNode(tree.left);
break;
}
}
if(tree.right!=null) {
if (tree.right.val == n) {
tree.right = nextNode(tree.right);
break;
}
}
if(tree.val<n)
tree = tree.left;
else
tree = tree.right;
}
}
//找到删除之后的备胎
private static FindTree nextNode(FindTree tree){
if(tree.left==null&&tree.right==null)
return null; //第一种情况 删除的节点左右孩子都是空
else if(tree.left==null)
return tree.right; // 第二种情况左孩子空
else if(tree.right==null)
return tree.left; //第三种情况右孩子空
else { //第四种情况
FindTree now = tree.right;
if(now.left==null){
now.left = tree.left;
return now;
}
else{
while(now.left.left!=null)
now = now.left;
FindTree temp = now.left;
now.left = null;
temp.left = tree.left;
temp.right = tree.right;
return temp;
}
}
}
}
查找和增加的算法都很常规,删除稍微复杂点:
删除的思路是:找到删除的那个节点,保存它的父节点。让父节点指向新的删除完的子树
删除的节点情况分为:
删除的节点左右孩子都是空的,直接让父节点指向null
删除的节点左孩子为空,右不空,让父节点指向右子树
删除的节点左孩子不为空,右空,让父节点指向左子树
删除的节点左右都不为空,这时候应当找到右子树的最小节点,来“继承“被删除的节点
所以 又有如下两种情况 :一是子树没有左边分支,也就是下图中40就是最小的 二是有左边的分叉,这时38就是最小的
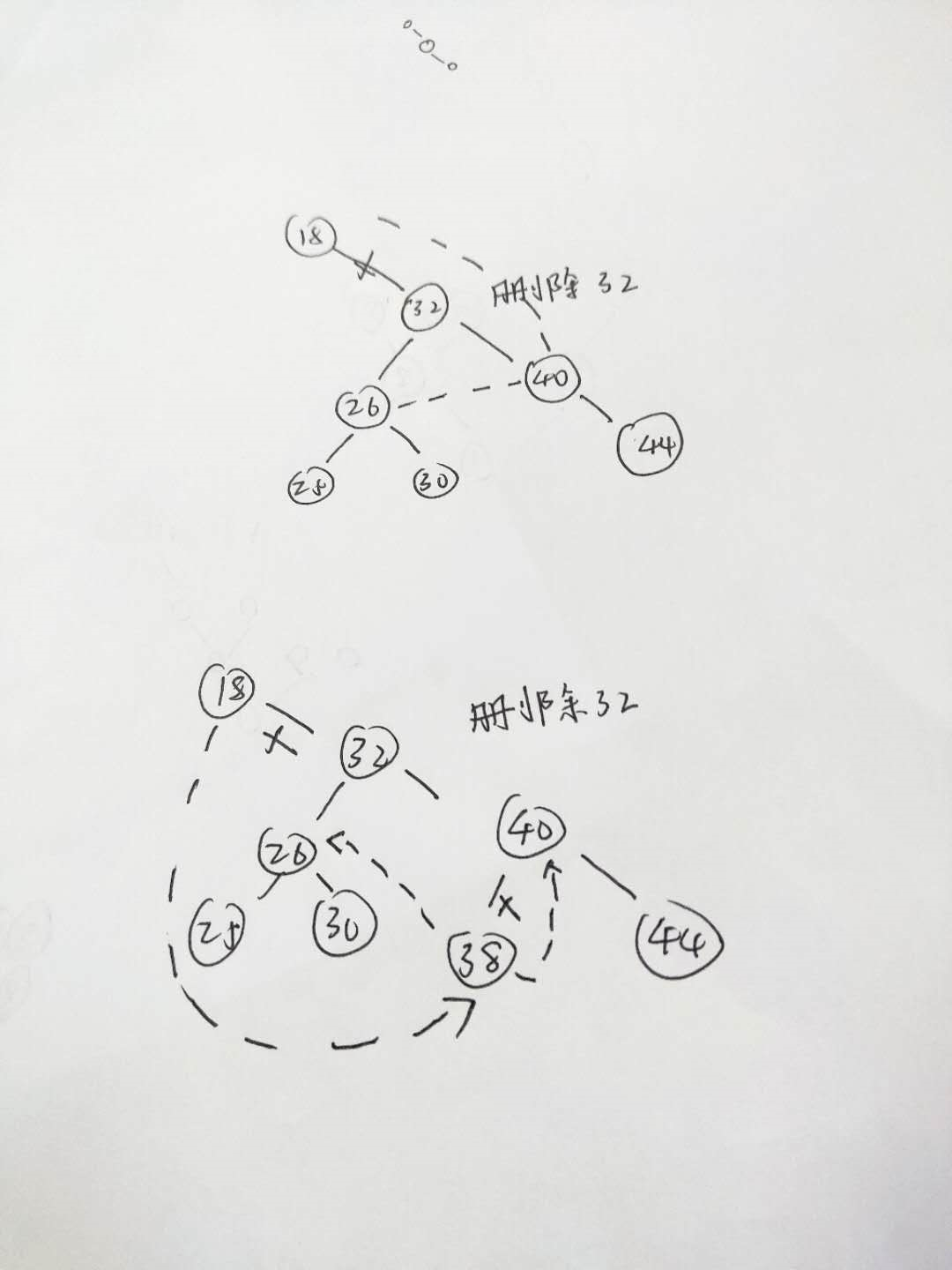
另外 由于整个类的定义问题,删除根节点的操作没法实现,因为我这里把根节点作为参数了,java又是值传递,所以我另写了一个方法实现
起始 就是调用找备胎节点的方法就行了
public static FindTree deleteRoot(FindTree tree){
return nextNode(tree);
}
测试如下:
public class TreeTest {
public static void main(String[] args) {
FindTree findTree = new FindTree(18);
FindTree.insert(findTree, 32);
FindTree.insert(findTree, 26);
FindTree.insert(findTree, 25);
FindTree.insert(findTree, 30);
FindTree.insert(findTree, 40);
FindTree.insert(findTree, 44);
FindTree.showTree(findTree);
System.out.println();
FindTree.showTree1(findTree);
FindTree.deleteNode(findTree, 32);
System.out.println();
FindTree.showTree(findTree);
System.out.println();
FindTree.showTree1(findTree);
}
}

二 、二叉堆(大根堆、小根堆)
二叉堆逻辑上是一颗树,满足根节点是最值,根节点是整颗树最小(大)的,左节点是整颗左子树最(小)的。
二叉堆逻辑上是一颗完全二叉树,一般用数组就可以实现。二叉树的一个应用堆排序,主要最核心的两个操作是:首先增加一个元素,一般到添加到尾部,此时要对数组进行上浮操作;其次是删除一个元素,这里只实现删除最值元素,
也就是最值元素,此时把最后一个元素调到第一次,执行下坠操作。这部分漫画算法里讲的很好,下面是代码实现的一个二叉堆的结构:
public class MyHeap {
private int arr[];
int size;
MyHeap() {
this(20);
} //不指定堆的大小,就自定义为20
MyHeap(int n) {
arr = new int[n];
}
public boolean isEmpty(){
return size == 0;
} //当前堆是不是空的
public void push(int n) {
if(size==arr.length){
throw new RuntimeException("堆满了");
}
arr[size] = n;
int child = size;
int par = (child - 1) / 2;
int temp = arr[child];
while (child > 0 && temp < arr[par]) {
arr[child] = arr[par];
child = par;
par = (child - 1) / 2;
}
arr[child] = temp;
size++;
}
//弹出arr[0]的元素 并把尾部的元素调到arr[0] 执行下坠操作
public int pop(){
int now = arr[0];
int temp = arr[size-1];
int left = 1;
int par = 0;
while(left<size-1){
if(left==size-2){
if(temp<arr[left])
break;
}else{
if(temp<arr[left]&&temp<arr[left+1])
break;
}
if(left!=size-2&&arr[left]>arr[left+1]){
left++;
}
arr[par] = arr[left];
par = left;
left = 2 * par + 1;
}
arr[par] = temp;
size--;
return now;
}
}
public class TreeTest {
public static void main(String[] args) {
// FindTree findTree = new FindTree(18);
// FindTree.insert(findTree, 32);
// FindTree.insert(findTree, 26);
// FindTree.insert(findTree, 25);
// FindTree.insert(findTree, 30);
// FindTree.insert(findTree, 40);
// FindTree.insert(findTree, 44);
//
// FindTree.showTree(findTree);
// System.out.println();
// FindTree.showTree1(findTree);
// FindTree.deleteNode(findTree, 32);
// System.out.println();
// FindTree.showTree(findTree);
// System.out.println();
// FindTree.showTree1(findTree);
MyHeap heap = new MyHeap(20);
heap.push(2);
heap.push(10);
heap.push(1);
heap.push(20);
heap.push(-5);
heap.push(-5);
while(!heap.isEmpty()){
System.out.println(heap.downAdjust());
}
}
}
测试结果如下: