Deep Learning学习随记(一)稀疏自编码器
最近开始看Deep Learning,随手记点,方便以后查看。
主要参考资料是Stanford 教授 Andrew Ng 的 Deep Learning 教程讲义:http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial。这个讲义已经有人翻译了(赞一个),可以参见邓侃的新浪博客http://blog.sina.com.cn/s/blog_46d0a3930101h6nf.html。另外,博客园里有一个前辈关于讲义中练习的一系列文章,在具体实现时可以参照下:http://www.cnblogs.com/tornadomeet/category/497607.html
讲义从稀疏自编码(Sparse Autoencoder)这一章节开始讲起。前面三节是神经网络、BP神经网络以及梯度检验的方法。由于还有点神经网络的相关知识,这部分不是太难懂。就从自编码器和稀疏性(Autoencoders and sparisity)记起吧。
稀疏自编码器构建:
假设我们只有一个没有类别标签的训练样本集合{x(1),x(2)...},一个自编码神经网络就是一种非监督学习算法,它使用BP算法,并将目标值设为输入值(y(i)=x(i))。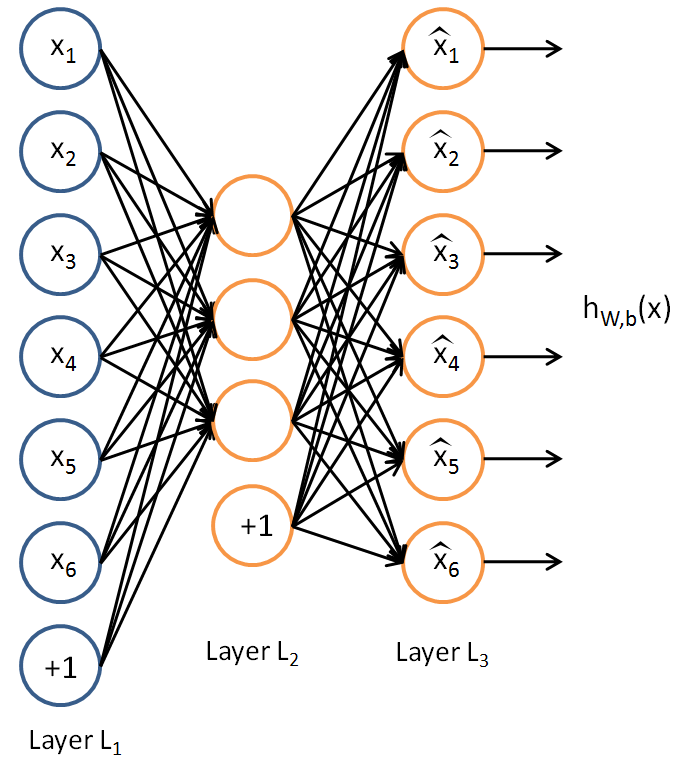
我们的目标是希望得到hW,b(X)≈x。用aj(2)(x)表示输入向量x对隐藏层单元j的激活值。则j的平均激活值:
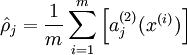
为了达到稀疏性,也即用最少(最稀疏)的隐藏单元来表示输入层的特征,我们希望所有隐藏层单元平均激活值接近于0.于是应用KL距离:
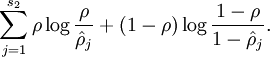
其中为了方便书写:![]() 。
。
其中 是稀疏参数,一般来说选一个很小的数,如0.05。
是稀疏参数,一般来说选一个很小的数,如0.05。
这样,神经网络整体代价函数就可以表示为: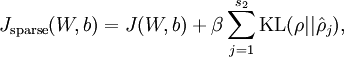 ,其中J(W,b)在前面BP网络章节中介绍过。
,其中J(W,b)在前面BP网络章节中介绍过。
讲义中同时给出了这种情况下如何计算用于偏导数计算的残差,自己懒得去推导了,直接拿来用就好了:
将反向传导过程中残差计算公式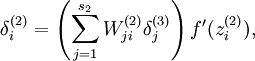 改为:
改为: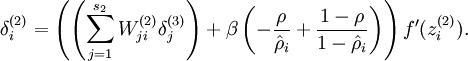 即可。
即可。
这样,一个稀疏自编码器就完成了。
个人感觉这个跟PCA貌似有点类似,可以将数据的维度降到很低(稀疏性嘛,用几个有用的隐层就可以表示出原始数据)。从Visualizing a Trained Autoencoder这节的结果来看,应该是这么个情况。
练习:
讲义中还给出了一个Exercise,Matlab用的不熟啊,这里去看了tornadomeet的博文http://www.cnblogs.com/tornadomeet/archive/2013/03/20/2970724.html,里面将代码实现了(膜拜下~),自己下下来跑了一下,结果什么的都跟原来博文一样(废话了,同一个程序,哈哈),最后没有收敛,迭代400次终止了。同时发现matlab貌似有点好用啊。。。这么几行代码就实现了,让我这用惯了C的情何以堪...回去自己补一下matlab了。



