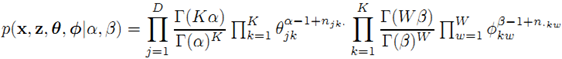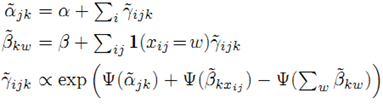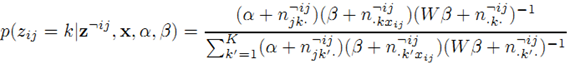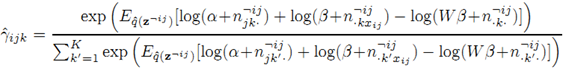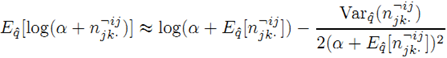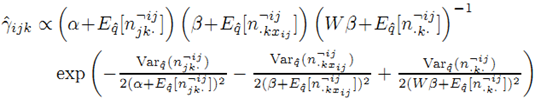[本文链接：http://www.cnblogs.com/breezedeus/archive/2013/01/20/2868930.html，转载请注明出处。]
LDA是个generative model，它首先从Dirichlet分布Dir(β)中抽取每个topic对应的参数
，然后语料集D中第j篇文档
的产生方式如下：
1. 选择文档长度： N ~ Poission(ξ) ；
2. 选择文档参数： θ ~ Dir(α) ；
3. 按照以下方式选取文档中的每个词
：
(a) 选择一个topic：
(b) 从W个词中选取出此词：
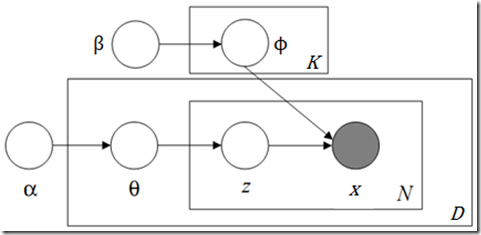
LDA的图表示如下，其中z、θ和Φ为隐藏变量，α和β为超参数。
利用上面LDA的产生假设，可以得到x、z、θ和Φ的联合分布为：
其中
，
和
。
为了最大化
，常用的方法就是基于Variational Bayes（简称VB，也叫Variational EM）的mean field近似方法，这也是LDA最初提出时作者使用的求解方法[1]。这种方法在Graphical models用的很多，不熟悉的同学可以参考我在学校时写的一个介绍pdf。记z、θ和Φ的后验分布的mean fields近似为：
其中
为Multinomial分布，而
都是Dirichlet分布。容易验证下面的不等式成立：
其中
。
VB通过最小化variational free energy 
来获得
中对应的参数估计：
其中
为digamma函数。
上面最后面那个式子里有一个很重要的地方需要说明下。我们之前的产生模型里，在一个文档里，不同位置的相同词（i为第几个词的下标）是可能有不同的后验分布的，但从上面最后的公式中可以看出式子右边与i有关的只有
，也即只与第i个位置的具体词是什么有关。所以在使用VB求解时，我们只需要考虑与具体词相关的
，这样在一个文档中多次重复的词只需要算一遍就行了。 详细的推导可见[1]。
之后，又有很多工作提出了一些其他求解方法[2, 3, 4]。例如[2]中作者提出的Collapsed Gibbs Sampling (CGS) 算法中，首先把隐变量θ和Φ积掉，然后得到如下x和z的联合分布：
然后在固定其他变量值的条件下，
的条件概率为：
其中的¬ij表示在对应计算中删除
和
带来的影响。通过这个条件概率式子，再利用Gibbs Sampling方法进行迭代抽样，最终我们可以得到需要的参数估计值。 详细的推导可见[2, 9]。
Gibbs Sampling的问题是收敛比较慢，而且很难判断何时已达到收敛。[3]中作者建议使用VB代替[2]中的Gibbs Sampling进行求解（所以称为Collapsed VB，简称CVB），也即最小化：
对应的参数估计为：
精确计算上式中的期望项计算量比较大。因为
，所以可以把它看成是多个Bernoulli分布的和，进而用Gaussian分布就可以很好地近似它。其Gaussian近似的均值和方差分别为：
另一方面，对log(α+x)利用Taylor展开到第二项作为它的近似：
融合这两个近似，得到如下近似：
把这个近似带入到前面的
表达式中，得到：
[5]中作者建议在CVB中对log(α+x)进行近似时只使用一阶近似，也即：
从而推导出下面的参数公式：
这个方法被称为CVB0。
在获得了
后，CVB和CVB0使用与VB中相同的表达式获得隐藏变量θ和Φ对应的后验分布。所以，测试集的概率可以使用下式计算得到：
注意，上面第一个式子就是根据LDA的模型产生方式获得的，只是对应的分布换成了后验分布。详细的推导可见[3]。
[5]中作者对以上各种算法做了比较详细的比较，他们发现在超参数α和β选取得比较合适时，这些算法的效果差别并不大。较之其他算法，CVB0需要的内存量和计算量都占优，所以[5]中作者最终推荐实际应用中使用CVB0。最近几年又有些工作进一步探讨了不同情况下（如在线学习）如何高效地学习LDA，感兴趣的同学可见[6, 7]。
我们上面的讨论都一直未提及超参数的学习方法，只是简单假设它们是选定不变的。[5]中作者也实验了两种超参数调整的方法：
1. 使用[8]中建议的固定点迭代方法更新超参数，具体可见[5, 7, 8]；
2. 利用测试集，使用网格搜索的方式找出最优的超参数取值。
另外，[1]中作者也建议使用Newton-Raphson方法来学习超参数的取值。
[References]
[1] Blei, D., Ng, A., and Jordan,M. (2003). Latent Dirichlet allocation. Journal of Machine Learning Research, 3:993–1022.
[2] T. L. Griffiths and M. Steyvers. Finding scientific topics. In PNAS, 2004.
[3] YeeWhye Teh, David Newman, and MaxWelling. A collapsed variational Bayesian inference algorithm for latent Dirichlet allocation. In Advances in Neural Information Processing Systems 19, 2007.
[4] Thomas Minka and John Laffert. Expectation-Propagation for the Generative Aspect Model, 2002.
[5] A. Asuncion, M. Welling, P. Smyth, and Y. W. Teh. On smoothing and inference for topic models. In Proceedings of the International Conference on Uncertainty in Artificial Intelligence, 2009.
[6] Matthew D. Hoffman, David M. Blei and Francis Bac. Online Learning for Latent Dirichlet Allocation, 2010.
[7] Issei Sato, Kenichi Kurihara and Hiroshi Nakagawa. Deterministic Single-Pass Algorithm for LDA, 2010.
[8] Thomas P. Minka. Estimating a dirichlet distribution. Technical report, Microsoft, 2000.
[9] Gregor Heinrich. Parameter estimation for text analysis. Technical report, 2005.
