B-树小结汇总
本文很多内容均来源于网络，经过修改，因来源众多，不一一指出
当查找的文件较大，且存放在磁盘等直接存取设备中时，为了减少查找过程中对磁盘的读写次数，提高查找效率，基于直接存取设备的读写操作以"页"为单位的特征。
1972年R.Bayer和E.M.McCreight提出了一种称之为B-树的多路平衡查找树。它适合在磁盘等直接存取设备上组织动态的查找表。
1、定义与特性
B-树是一种平衡的多路查找树，在文件系统中有所应用。主要用作文件的索引。
B-树结构特性：
一棵m阶B-树，或为空树，或为满足下列特性的m叉树：(m≥3)
(1)根结点只有1个，关键字字数的范围[1,m-1]，分支数量范围[2,m]；
(2)除根以外的非叶结点，每个结点包含分支数范围[[m/2],m]，即关键字字数的范围是[[m/2]-1,m-1]，其中[m/2]表示取大于m/2的最小整数；
(3)非叶结点是由叶结点分裂而来的，所以叶结点关键字个数也满足[[m/2]-1,m-1]；
(4)所有的非终端结点包含信息：(n，P0，K1，P1，K2，P2，……，Kn，Pn)，
其中Ki为关键字，Pi为指向子树根结点的指针，并且Pi-1所指子树中的关键字均小于Ki，而Pi所指的关键字均大于Ki（i=1，2，……，n），n+1表示B-树的阶，n表示关键字个数，即[ceil(m / 2)-1]<= n <= m-1；
(5)所有叶子结点都在同一层，并且指针域为空，具有如下性质：
根据B-树定义，第一层为根有一个结点，至少两个分支，第二层至少2个结点，i≥3时，每一层至少有2乘以([m/2])的i-2次方个结点([m/2]表示取大于m/2的最小整数)。若m阶树中共有N个结点，那么可以推导出N必然满足N≥2*(([m/2])的h-1次方)-1 (h≥1)，因此若查找成功，则高度h≤1+log[m/2](N+1)/2，h也是磁盘访问次数(h≥1)，保证了查找算法的高效率。
从以上的定义特性可总结出如下结论:对于m阶B-树
2)除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3)若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4)所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素）。
5)每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
a) Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。
b) Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
c) 关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。
6)每个结点能包含的关键字的个数有一个上界和下界。这些界可以称为B-树的相应结点的最小度数(内结点中结点最小孩子数目，即前面提到指针P的个数)的固定整数t>=2来表示
a).每个非根结点必须至少有t-1个关键字，每个非根的内结点至少有t个子女,即。如果树是非空的，则根结点至少包含一个关键字。
b).每个结点可包含至多2t-1个关键字，每个非根的内结点至多可有2t个子女。如果一个结点是满的，则它有2t-1个关键字.
c).综上根节点关键字的个数范围: [1, 2*t - 1]，非根节点关键字的个数范围: [t-1, 2*t - 1]
下图给出了典型的3阶B-树
B-树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据
以上定义特性均为网上资料综合而来，下面给出对于分支关键字个数以及度数的范围简要总结：
一个m阶B-树：
1).对于根节点，子树(孩子或者称为分支)个数取值范围[2,m]，关键字个数范围[1,m-1]
2).对于内结点，分支数范围[ceil(m/2),m]，关键字个数的范围是ceil(m/2)-1,m-1]
3).对于最小度数为t>=2的结点，根节点关键字的个数范围: [1, 2*t - 1]，非根节点关键字的个数范围: [t-1, 2*t - 1]，分支的个数范围：[t, 2*t]
PS 关于最小度数的理解：个人理解为对于m阶B-树t=ceil(m/2)
B-树定义的结点
#define MAXM 10 /*定义B-树的最大的阶数*/
typedef int KeyType; /*KeyType为关键字类型*/
typedef struct BTNode /*B-树结点类型定义*/
{
int keynum; /*结点当前拥有的关键字的个数*/
KeyType key[MAXM]; /*key[1..keynum]存放关键字,key[0]不用*/
struct BTNode *parent; /*双亲结点指针*/
struct BTNode *ptr[MAXM]; /*孩子结点指针数组ptr[0..keynum]*/
}BTTree;
2.B-树复杂度与高度
它的高度是
(这个是网上给的结果，与后面推导的结果有异议)，而不是其它几种树的H=log2n,其中T为度数（每个节点包含的元素个数），即所谓的阶数，n为总元素个数或总关键字数。
上面B树高度的公式也可以进行推导得出，将每一层级的的元素个数加起来，比如度为T的节点，根为1个节点，第二层至少为2个节点，第三层至少为2t个节点，第四层至少为2t*t个节点。将所有最小节点相加，推导过程：n>=1+2t+2t*t+2t3+.....+2th-1=1+2t(1+t+t*t+t3+....+th-2)=1+2t*(th-1-1)/(t-1)>=1+2(t-1)*(th-1-1)/(t-1) |最后一个不等式推出的原因：t>=2
最后推出结果h<=logt((n+1)/2)+1
网上给的公式是 
但是个人感觉推导并不严密，而且中间似乎有错误,结果我也没推出来和他们一样的 ，不知道什么缘故 如果笔者推算错误 希望指出
关于时间复杂度借用网上给出的过程不过都没有给出解释，其中M为设定的非叶子结点最多子树个数，N为关键字总数；所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；
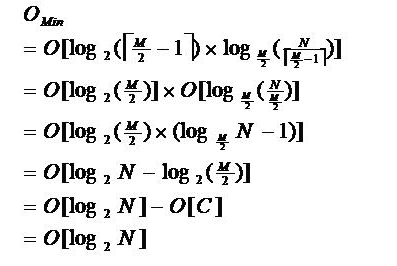
2.基本操作
这里只给出插入删除操作，查找操作相对简单的多 这里不做解释
1)B-树的插入操作(重点判断是否满足n<=m-1)
a.利用前述的B-树的查找算法查找关键字的插入位置。若找到，则说明该关键字已经存在，直接返回。否则查找操作必失败于某个最低层的非终端结点上。
b.判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足，则说明该结点还有空位置，直接把关键字k插入到该结点的合适位置上。若不满足，说明该结点己没有空位置，需要把结点分裂成两个。
分裂的方法是：生成一新结点。把原结点上的关键字和k按升序排序后，从中间位置把关键字（不包括中间位置的关键字）分成两部分。左部分所含关键字放在旧结点中，右部分所含关键字放在新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过（m-1），则要再分裂，再往上插。直至这个过程传到根结点为止。
2).B-树的删除操作(重点判断删除所在结点及其兄弟结点，父结点中n>ceil(m/2)-1，n=ceil(m/2)-1，n<ceil(m/2)-1)
在B-树上删除关键字K的过程也可以分为两步完成
a.利用前述的B-树的查找算法找出该关键字所在的结点。然后根据 k所在结点是否为叶子结点有不同的处理方法。
b.若该结点为非叶结点，且被删关键字为该结点中第i个关键字key[i]，则可从指针son[i]所指的子树中找出最小关键字Y，代替key[i]的位置，然后在叶结点中删去Y。因此，把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了。
在B-树叶结点上删除一个关键字的方法是
首先将要删除的关键字 k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理，共有三种可能情况：
a.如果被删关键字所在结点的原关键字个数n>=ceil(m/2)，说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单，只需从该结点中直接删去关键字即可。
b.如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1，说明删去该关键字后该结点将不满足B-树的定义，需要调整。
调整过程为：如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上移关键字的关键字下移至被删关键字所在结点中。
c.如果左右兄弟结点中没有“多余”的关键字，即与该结点相邻的右（左）兄弟结点中的关键字数目均等于ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字Ki一起，合并到Ai（即双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于ceil(m/2)-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。
总之，设所删关键字为非终端结点中的Ki，则可以指针Ai所指子树中的最小关键字Y代替Ki，然后在相应结点中删除Y。对任意关键字的删除都可以转化为对最下层关键字的删除。
如图示：
a、被删关键字Ki所在结点的关键字数目不小于ceil(m/2)，则只需从结点中删除Ki和相应指针Ai，树的其它部分不变。
b、被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1，则需调整。调整过程如上面所述。
c、被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1，假设该结点有右兄弟，且其右兄弟结点地址由其双亲结点指针Ai所指。则在删除关键字之后，它所在结点的剩余关键字和指针，加上双亲结点中的关键字Ki一起，合并到Ai所指兄弟结点中（若无右兄弟，则合并到左兄弟结点中）。如果因此使双亲结点中的关键字数目少于ceil(m/2)-1，则依次类推.
