CSharpGL(13)用GLSL实现点光源(point light)和平行光源(directional light)的漫反射(diffuse reflection)

CSharpGL(13)用GLSL实现点光源(point light)和平行光源(directional light)的漫反射(diffuse reflection)

 

2016-08-13

 

由于CSharpGL一直在更新，现在这个教程已经不适用最新的代码了。CSharpGL源码中包含10多个独立的Demo，更适合入门参考。

 

为了尽可能提升渲染效率，CSharpGL是面向Shader的，因此稍有难度。

 

 

 

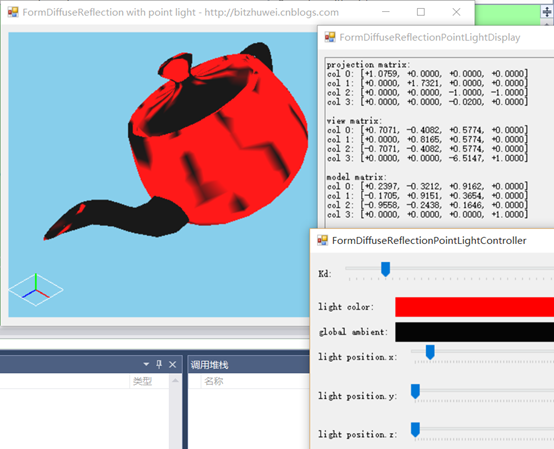
光源

如何用GLSL实现点光源和平行光源等各类光源的效果？这个问题我查找资料、思考了很久，今天终于解决了一部分。

漫反射(diffuse reflection)是粗糙表面的反射效果。理论上的粗糙表面，对各个方向的反射效果都完全相同。本篇就分别实现点光源(point light)和平行光源(directional light)照射到粗糙表面时产生的漫反射效果。

下载

这个示例是CSharpGL的一部分，CSharpGL已在GitHub开源，欢迎对OpenGL有兴趣的同学加入（https://github.com/bitzhuwei/CSharpGL）

点光源(point light)

讲GLSL当然要从shader开始说起。

Vertex shader

#version 150 core

in vec3 in_Position;
in vec3 in_Normal;
out vec4 pass_Position;
out vec4 pass_Color;
uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projectionMatrix;
uniform vec3 lightPosition;
uniform vec3 lightColor;
uniform vec3 globalAmbient;
uniform float Kd;

void main(void)
{
    gl_Position = projectionMatrix * viewMatrix * modelMatrix * vec4(in_Position, 1.0f);
    vec3 worldPos = (viewMatrix * modelMatrix * vec4(in_Position, 1.0f)).xyz;
    vec3 N = (transpose(inverse(viewMatrix * modelMatrix)) * vec4(in_Normal, 1.0f)).xyz;
    N = normalize(N);
    // light's direction
    vec3 L = (viewMatrix * vec4(lightPosition, 1.0f)).xyz - worldPos;// point light
    L = normalize(L);
    // diffuse color from directional light
    vec3 diffuseColor = Kd * lightColor * max(dot(N, L), 0);
    // ambient color
    vec3 ambientColor = Kd * globalAmbient;
    pass_Color.xyz = diffuseColor + ambientColor;
    pass_Color.w = 1;
}

首先， gl_Position 的计算是不用解释了。

要计算漫反射下的点光源照射物体的效果，需要知道物体的顶点的法线(normal)、顶点位置到光源的方向(light direction)，两者夹角越小，那么光照越强。 max(dot(N, L), 0) 就是在计算光照强度。

为了避免全黑，我们加个环境光(ambient light)。环境光，就是那些综合起来的光照因素，不好准确计算，就简单地用一个 vec3 globalAmbient; 来描述了。

重要知识点

MVP的含义(projection * view * model)

那三个矩阵变换里，每个都有各自的意义。其中，modelMatrix是在物体坐标系旋转缩放平移模型。就好比父母在家里打扮自己的宝宝。ViewMatrix是把物体放到世界坐标系下，让摄像机为原点(0,0,0)，来观察模型。就好比把各家各户的宝宝放到幼儿园拍合影。ProjectionMatrix就是宝宝们的合影照片。

所以， (viewMatrix * modelMatrix * vec4(in_Position, 1.0f)).xyz 就是物体的顶点在世界坐标系的位置。也就是在场景中的位置。（不是在3dmax里的位置）

法线(normal)

但是，不能以此类推世界坐标系里的法线(normal)。法线从3dmax中的值变换到场景中后，它的值应该是 (transpose(inverse(viewMatrix * modelMatrix)) * vec4(in_Normal, 1.0f)).xyz （就是要求逆然后转置），而不是 (viewMatrix * modelMatrix * vec4(in_Normal, 1.0f)).xyz 。具体原因可参考这里（http://blog.csdn.net/racehorse/article/details/6664775）。或者

Normals are funny.  They're vec3's, since you don't want perspective on normals.   And they don't actually scale quite right--a 45 degree surface with a 45 degree normal, scaled by glScalef(1,0.1,1), drops the surface down to near 0 degrees, but actually tilts the normal *up*, in the opposite direction from the surface, to near 90 degrees.

Mathematically, if between two points a and b on the surface, dot(n,b-a)==0, then after applying a matrix M to the points, you want the normal to still be perpendicular.  The question is, what matrix N do you have to apply to the normal to make this happen?  In other words, find N such that
    dot( N * n , M * a - M * b) == 0

We can solve this by noting that dot product can be expresed as matrix multiplication--dot(x,y) = transpose(x) * y, where we treat an ordinary column-vector as a little matrix, and flip it horizontally.  So
   transpose(N * n) * (M*a - M*b) == 0         (as above, but write using transpose and matrix multiplication)
   transpose(N * n) * M * (a-b) == 0              (collect both copies of M)
   transpose(n) * transpose(N) * M * (a-b) == 0    (transpose-of-product is product-of-transposes in opposite order)

OK.  This is really similar to our assumption that the original normal was perpendicular to the surface--that dot(n,b-a) == transpose(n) * (a-b) == 0.  In fact, the only difference is the new matrices wedged in the middle.  If we pick N to make the term in the middle the identity, then our new normal will be perpendicular to the surface too:
    transpose(N) * M == I   (the identity matrix)
This is the definition for matrix inverses, so the "normal matrix" N = transpose(inverse(M)).

If you look up the GLSL definition for "gl_NormalMatrix", it's defined as "the transpose of the inverse of the gl_ModelViewMatrix".  Now you know why!

 

光源的位置

由于模型受到viewMatrix的影响，所以摄像机的改变也会改变模型的顶点位置，而点光源的位置如果不变，就会出现不同的光照结果。这不合实际。所以点光源也要按viewMatrix做变换。

Fragment shader

极其简单。

#version 150 core

in vec4 pass_Color;
out vec4 out_Color;

void main(void)
{
    out_Color = pass_Color;
}

 

平行光源(directional light)

评选光源与之类似。至于为何在计算平行光源的方向时要用 (transpose(inverse(viewMatrix * modelMatrix)) * vec4(in_Normal, 1.0f)).xyz 这种复杂的步骤，原理在上文的法线(normal)中科院找到。（提示：都是为了让摄像机对模型和对光源方向产生同样的变换，从而使得摄像机的移动不会改变光照效果。）

#version 150 core

in vec3 in_Position;
in vec3 in_Normal;
out vec4 pass_Position;
out vec4 pass_Color;
uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projectionMatrix;
uniform vec3 lightPosition;
uniform vec3 lightColor;
uniform vec3 globalAmbient;
uniform float Kd;

void main(void)
{
    gl_Position = projectionMatrix * viewMatrix * modelMatrix * vec4(in_Position, 1.0f);
    vec3 worldPos = (viewMatrix * modelMatrix * vec4(in_Position, 1.0f)).xyz;
    vec3 N = (transpose(inverse(viewMatrix * modelMatrix)) * vec4(in_Normal, 1.0f)).xyz;
    N = normalize(N);
    // light's direction
    vec3 L = (transpose(inverse(viewMatrix)) * vec4(lightPosition, 1.0f)).xyz;// directional light
    L = normalize(L);
    // diffuse color from directional light
    vec3 diffuseColor = Kd * lightColor * max(dot(N, L), 0);
    // ambient color
    vec3 ambientColor = Kd * globalAmbient;
    pass_Color.xyz = diffuseColor + ambientColor;
    pass_Color.w = 1;
}

Fragment shader与上文的相同。

试验

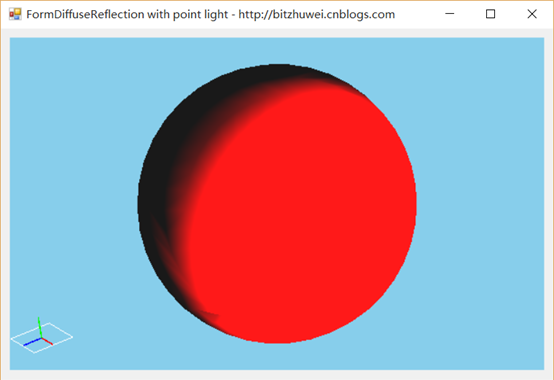
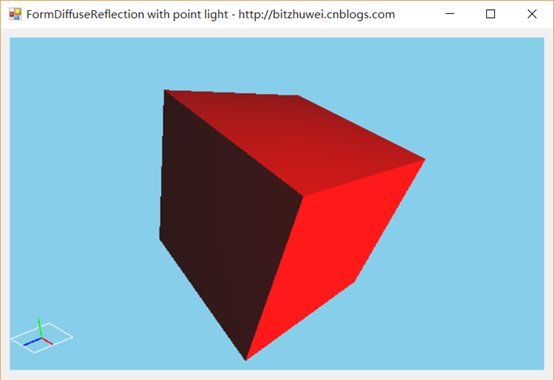
在一个场景中，一个点光源照射到物体上。如果物体旋转，那么光照效果会改变。如果光源位置改变，那么光照效果会改变。但是，如果摄像机改变位置，却不会改变漫反射的效果。（漫反射，反射到各个角度的光效是相同的，所以与摄像机位置无关。）

您可以下载此示例（https://github.com/bitzhuwei/CSharpGL）试验，鼠标左键旋转模型，光效会改变。鼠标右键旋转摄像机，光效是不变的。

 

总结

今后将继续整合一些镜面反射等类型的光照效果，为更多更强的shader效果做准备。

不得不说线性代数在计算机3D效果方面的应用彻底证明了它的强大。

学OpenGL有2年了，从NEHE到SharpGL，从《3D Math Primer for Graphics and Game Development》到《OpenGL Programming Guide》，算是对OpenGL有了初级的认识。最近我纠集整理了SharpGL，GLM，SharpFont等开源库，想做一个更好用的纯C#版OpenGL。欢迎对OpenGL有兴趣的同学加入（https://github.com/bitzhuwei/CSharpGL）