Tikhonov regularization 吉洪诺夫正则化

在求解反问题时，正则化技术的作用非常大。对于大多数优化问题，基本都使用了正则化方法。但是什么是正则化？却没有一个概念性的定义。

解释性的定义如下：

对于线性方程Ax=b，当解x不存在或者解不唯一时，就是所谓的病态问题(ill-posed problem). 但是在很多时候，我们需要对病态问题求解，那怎么做？

对于解不存在的情况，解决办法是增加一些条件找一个近似解；对于解不唯一的情况，解决办法是增加一些限制缩小解的范围。这种通过增加条件或限制要求求解病态问题的方法就是正则化方法。

正则化的英文是regularization，即规则化，调整。通过一些调整或者其他办法，使病态问题也能得到唯一解。在这个调整的过程中，使用的技术就是正则化技术，所用的方法就是正则化方法。

求解线性方程的标准方法是最小二乘法，即求解min||Ax-b||2，对于病态的线性方程，吉洪诺夫提出使用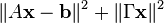方法，叫做吉洪诺夫矩阵（Tikhonov matrix）.