多变量微积分笔记9——极坐标下的二重积分

　　直角坐标是常用的坐标法，但是对于一些特别的问题，在直角坐标系下处理就显得有点笨拙了。这个时候，不妨试试极坐标。它可以使得问题变得出乎意料的简洁，也能让问题直观和清晰起来。

　　关于极坐标的相关问题可参考《数学笔记27——极坐标下的面积》

极坐标的积分域

　　在上一篇文章的“积分边界”一节有这样一个例子： z = 1 – x² – y²，如果约束 x² + y² ≤ 1且x ≥ 0，y ≥ 0，那么z的二重积分是什么？

　　R区是1/4圆：

　　现在我们尝试将其转换为极坐标来计算R区域，这将是半径r和夹角θ的函数：

 

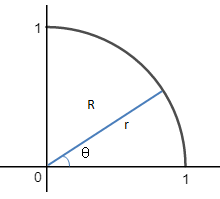
　　在绝大部分情况下，我们会使用θ作为外积分，r作为内积分；同时很容易确定二者的积分域：

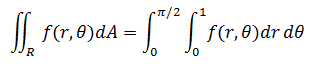
极坐标下的dA

　　还是使用黎曼和去解释积分，那么在极坐标下如何切割成小矩形？

 

　　如上图所示，阴影部分就是ΔA，这是个近似的矩形，设其宽度为Δr，长度近似于弧长：

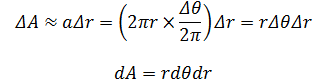
　　这就是在极坐标下的dA，它不在简单地等于dθdr，所以上一节的正确答案应该是：

 

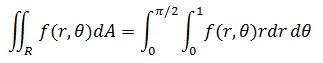
　　把原函数转换为极坐标后就可以计算积分了：

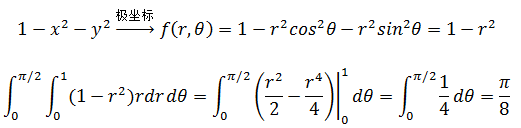
正态分布函数的积分

　　在概率论中经常使用正态分布函数，现在尝试求解它的积分：

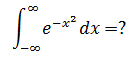
　　这是在单变量积分中很难计算的问题，只知道它最后将等于一个常数I。现在来看一个二重积分：

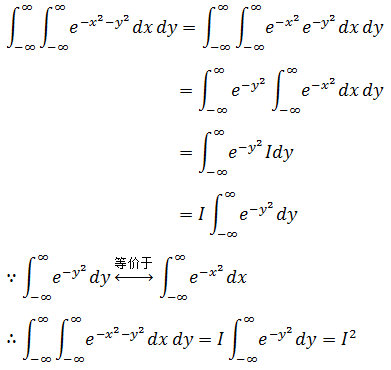
　　现在，问题变成了计算二重积分。貌似更复杂了，但是如果转换成极坐标，求解就会非常清晰。由于积分域是±∞，所以是对全空间的积分，因此可以将dr作为外积分。转换后的极坐标积分如下：

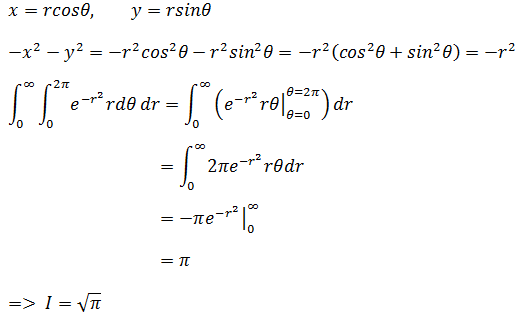
综合示例

示例1

　　 

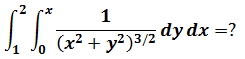
　　R区域：

 

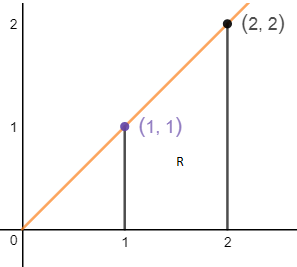
　　如果转换为极坐标，很容易判断θ的变换区域是0 ≤ θ ≤ π/4，需要计算的是r的积分域，如下图所示：

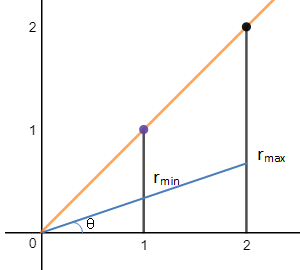
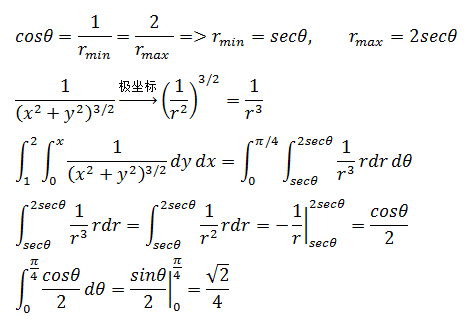
示例2

 　　

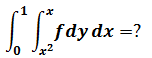
　　R区域：

 

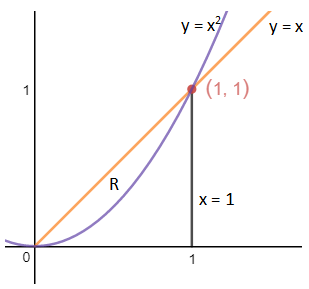
　　如果转换为极坐标，很容易判断θ的变换区域是0 ≤ θ ≤ π/4，r_min = 0

 

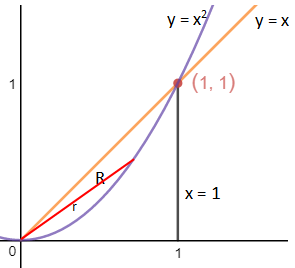
　　r_max实际上是r关于θ的函数，由于r的另一端总在y = x²上，所以转换为极坐标后：

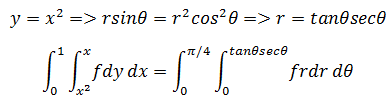
示例3

 　　

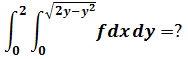
　　对于x的积分上限：

 

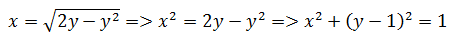
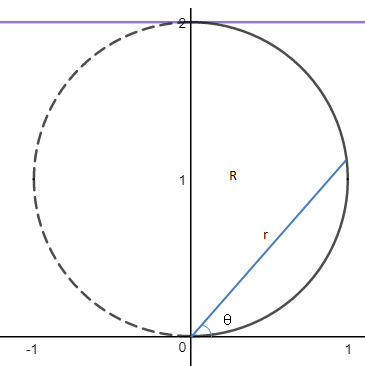
　　由此可见R区域是一个半圆。转换为极坐标后，0 ≤ θ ≤ π/2，r_min = 0，r_max是r关于θ的函数。

 

 

 

---

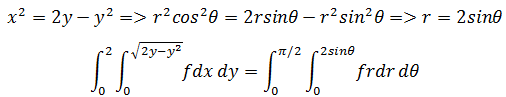
 　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”