线性代数笔记6——直线和曲线的参数方程
什么是参数方程
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x、y都是某个变数t的函数:

并且对于t的每一个允许的取值,由方程组确定的点(x, y)都在这条曲线上,那么这个方程就叫做曲线的参数方程,联系变数x、y的变数t叫做参变数,简称参数。相对而言,直接给出点坐标间关系的方程叫普通方程。
例如在运动学,参数通常是“时间”,而方程的结果是速度、位置等。用参数方程描述运动规律时,常常比用普通方程更为直接简便。对于解决求最大射程、最大高度、飞行时间或轨迹等一系列问题都比较理想。有些重要但较复杂的曲线(例如摆线),建立它们的普通方程比较困难,甚至不可能,有了参数方程,就可以很容易表达。
直线
空间中的直线
空间中两个平面的交集是一条直线,如果抛开平面,直线可以看作是点匀速直线运动的轨迹。
通过两点确定一条直线,此外,已知一点和与直线平行的向量也能确定一条直线。
直线的参数方程
一个点在空间中匀速直线运动,它在t = 0和t = 1时刻经过Q0 = (-1, 2, 2)和Q1 = (1, 3, -1)两点,Q(t)是该点关于时间t的函数:

如上图所示,点在t = 0时刻的位置Q0 = Q(0) = (-1, 2, 2),t = 1时刻的位置Q1 = Q(1) = (1, 3, -1),那么在任意t时刻,Q的位置Q(t)是哪里?

现在将问题转换为向量:

由于是匀速运动,所以运动距离与时间成正比:

随着时间的增长,向量也将增长。由于Q(t)是空间内的点,所以:

这就是该直线的参数方程,其来源是Q0Q(t) = tQ0Q1
如果t = 2,则在该时刻Q(2) = (3, 5, -4)
参数方程的几何解释
我们已经知道了直线参数方程的形式,现在看一下它的几何解释。
如果二维空间内有两个点(2,1)和(0,2),那么经过这两点的直线方程是什么?
初中的知识可以告诉我们,斜率是k = (y2 – y1)/(x2 – x1)。现在使用向量和参数方程来理解这个问题。假设在二维空间内有两个向量a<2,1>和b<0,2>,如下图所示:
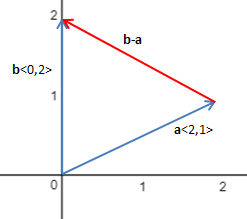
一个不太准确的说法是,将b-a的两端延长,就是所求的直线,只要能够恰当地表示这条直线就好了。由于向量表示的大小和方向的量,与位置无关,所以可以将b-a平移:
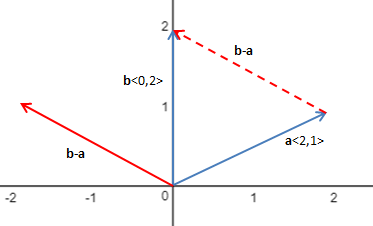
现在使用平移后的b-a,它与b的线性组合就可以表示所求直线(向量终点站直线上):
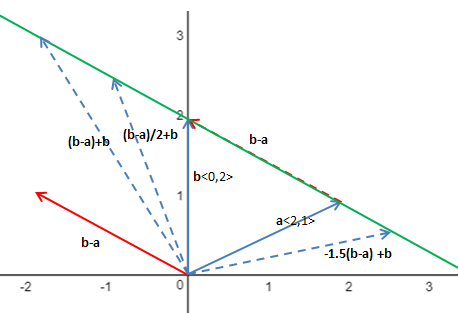
将b-a的倍数设为t,那么直线可以表示为:
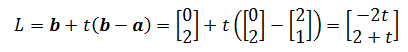
转换成x,y的参数方程,x = -2t, y = 2 + t
直线与平面的关系
上面的两个点Q0 = (-1, 2, 2)和Q1 = (1, 3, -1)对于平面x + 2y + 4z = 7来说,位置关系是什么?在平面的两侧还是一侧?是否在平面上?
将Q0和Q1代入平面方程:

由此可见Q0和Q1不在平面上,它们分属于平面两侧,向量Q0Q1将穿过平面,与平面有唯一的交点,这个交点又是什么?
上节已经求得了直线的参数方程Q(t) = (2t-1, t+2, -3t+2),直线与平面的交点将满足:

将直线参数方程代入平面方程也可能出现有无数解或无解的情况,此时直线与平面没有唯一交点,直线可能在平面上或与平面平行。
总结一下,把直线方程Q(t) = (x(t), y(t), z(t))代入平面方程ax + by + c = d,如果能计算出t的唯一值,直线穿过平面;如果得到一个等于d的常数,则直线在平面上;如果得到一个不等于d的常数,则直线与平面平行。
曲线
对于平面或空间内的任意运动,同样可以用参数方程表示。
摆线的参数方程
摆线是一种有名的曲线,它描述了当车辆匀速直线运动时,车轮上点的运动轨迹。如下图所示,P是半径为a的车轮边缘上的一点,刚开始时在原点,当车轮向右滚动后,P点将随之转动:

我们关注的问题是车轮滚动后P的轨迹,也就是t时刻P点的位置。如果P点是位置关于时间的函数,用参数方程可以表示为Q(t) = (x(t), y(t))。这意味着从时间的角度来表示位置,然而时间并非最好的参变量,因为P的轨迹是与时间无关的,即使车速变快,P的运动轨迹也不会改变。我们注意到,当车轮匀速运动时,P的角度和时间成正比:

∠θ和运动时间成正比,如果θ超过2π,则相当于开始了一个新的周期,对于角度的运算,3π和π是相同的。由此,可以将时间替换为角度,也就是使用车轮转动角度做参变量将得到更简单的答案:


将车轮转换为上图所示的向量(向量可参考《线性代数笔记2——向量(向量简介)》),则向量OP的参数方程就可以表示P点的运动轨迹。

由于车轮是沿着地面转动,且最初P的位置与O相同,所以在第一圈时,OA = PA的弧长(我承认在画图时比较随意,看起来它们并不相等):

实际上,无论第几圈,上式都成立。由于已经知道了OA和AB的长度,可以得出相应的向量:

现在只需要求出向量BP即可。这里并不需要知道点B和点P的坐标,由于向量只描述了大小和方向,所以向量和具体位置无关,因此可以通过将向量BP平移求得BP:


最终:


摆线的斜率
在车轮滚动一圈后,点P回到x轴,开始进入下一个周期,两个周期相交于一点。有一个值得关注的问题是,如果在该点处作轨迹曲线的切线,切线的斜率是什么?如下图所示,就是计算P5处轨迹曲线的切线:

为了简化问题,将当车轮看作单位圆,此时a = 1,

在P5处,θ=2π,斜率:

此时没有意义,但可以计算极限:

因此,在P5处,斜率趋近于∞,也就是有一条垂直于x轴的切线。
也可以使用泰勒展开式计算斜率(泰勒级数可参考《数学笔记31——幂级数和泰勒级数》):

示例
示例1
两条直线L1和L2是否相交,如果相交,其交点是什么?

可以用以往的知识将参数方程转换为普通方程:

方程组有唯一解,x = 1, y = 2,两条直线相交于(1, 2)
也可以直接用参数方程求解。如果两条直线相交,参数方程组有唯一解:

将解代入参数方程:

两条直线相交于(1, 2)
示例2
直线L经过P(0, -1, 1)和Q(2, 3, 3)两点,直线与平面2x + y – z = 1的关系?
设直线方程是L(x(t), y(t), z(t)),则:

将L的参数方程代入平面方程:

t有唯一解,指向与平面相交。将t代入直线的参数方程,交点是(1, 1, 2)
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号