单变量微积分笔记19——数值积分
什么是数值积分
数值积分是计算定积分数值的方法和理论。在数学分析中，给定函数的定积分的计算不总是可行的。许多定积分不能用已知的积分公式得到精确值。数值积分是利用黎曼积分等数学定义，用数值逼近的方法近似计算给定的定积分值。借助于电子计算设备，数值积分可以快速而有效地计算复杂的积分。
数值积分的必要性源自计算函数的原函数的困难性。利用原函数计算定积分的方法建立在牛顿-莱布尼兹公式之上。然而，原函数可以用初等函数表示的函数为数不多，大部分的可积函数的积分无法用初等函数表示，甚至无法有解析表达式。例如常见的正态分布函数：
的原函数就无法用初等函数表示。
不仅如此，在很多实际应用中，只能知道积分函数在某些特定点的取值，比如天气测量中的气温、湿度、气压等，医学测量中的血压、浓度等等。另外，积分函数有可能是某个微分方程的解。由于很多微分方程只能数值求解，因此只能知道函数在某些点上的取值。这时是无法用求原函数的方法计算函数的积分的。
另外，当积分区域是曲面、三维形体以至于高维流形时，牛顿-莱布尼兹公式不再适用，只能使用更广泛的格林公式或斯托克斯公式，以转化为较低维数上的积分，但只能用于少数情况。因此，只能使用数值积分计算函数的近似值。
数值积分的常见公式
矩形公式
就是常见的黎曼和，在切割小矩形时，可选择使用左矩形或右矩形。
左矩形公式：
右矩形公式：
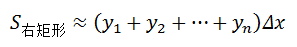
左右矩形公式的区别如下图所示：
左矩形公式
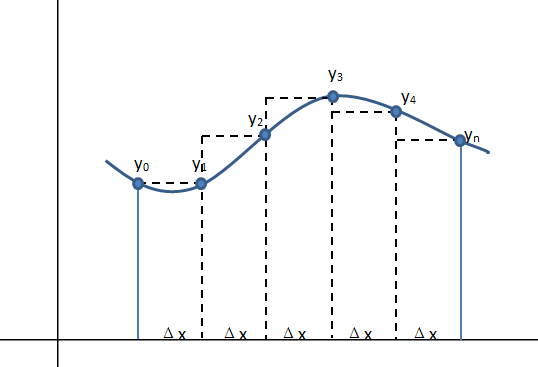
右矩形公式
梯形公式
与矩形公式不同，梯形公式直接将点连接，当Δx→∞时，这看起来更接近于与真实面积：
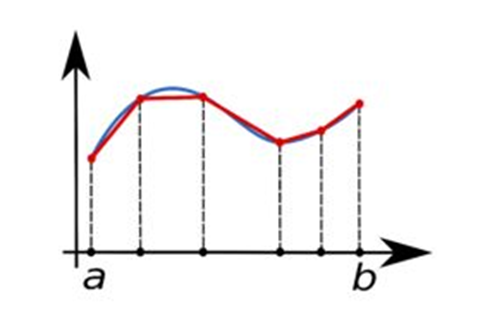
辛普森公式
辛普森公式是更高级并且在实际中精确度更高的公式，它的核心思想是面积≈ 底边长 × 平均高度。高度是有权重的，为了计算平均高度，试图将点用抛物线相连，每个抛物线连接三个相邻的点：
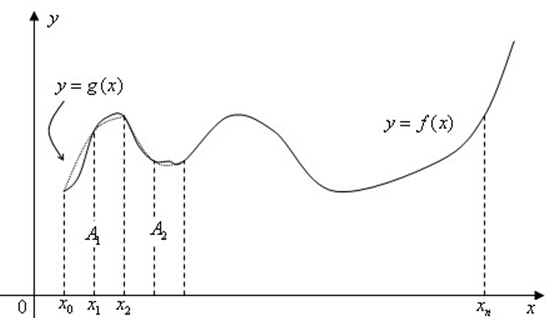
这里直接给出结果。上图从x0到x2的面积可计为：
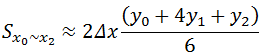
总面积：
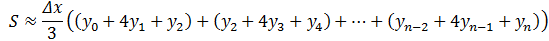
数值积分的应用
示例1
计算y = 1/x在x = 1和 x = 2之间与x轴围成的面积：
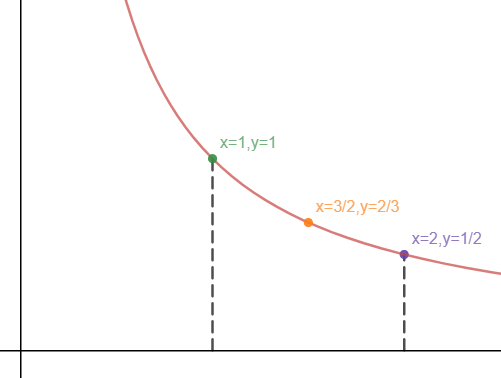
下面是不同计算方法的对比。
实际面积：
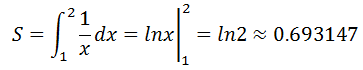
梯形公式：
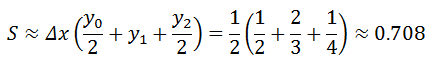
辛普森公式：
这个例子中，辛普森公式远比梯形公式精确，实际上，|真实值 – 辛普森值| ≈ (Δx)4，如果Δx = 0.1，辛普森值将非常接近真实值。
示例2
用梯形公式和辛普森公式估算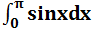 
，Δx=π/4
梯形公式：
辛普森公式：
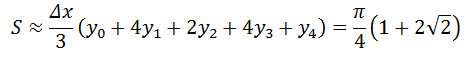
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
