线性代数笔记2——向量（向量简介）
什么是向量
在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的只有大小，没有方向的量叫做数量（物理学中称标量）。
如果用Rn表示n个实数的有序集，Rn中的一个向量就是一个n元有序组，Rn = {(x1, x2,……xn) | xi ∈ R}
向量的记法：印刷体记作粗体的字母（如a、b、u、v），书写时在字母顶上加一小箭头“→”。如果给定向量的起点（A）和终点（B），可将向量记作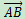
。实际上向量有多种记法，可以用元组表示一个向量，如 (x1, x2) 或 < x1, x2>。在线性代数中，n元向量可以用n×1矩阵表示，如：
向量中的每个元素xn，都称作向量的一个分量。
向量的模
向量的模即向量的长度，如果A是n维向量，则A的模标记为：
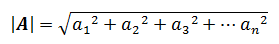
单位向量和零向量
单位向量
单位向量是指模等于1的向量。由于是非零向量，单位向量具有确定的方向。单位向量有无数个。
一个非零向量除以它的模，可得所需单位向量。一个单位向量的平面直角坐标系上的坐标表示可以是：(n,k) ，则有n²+k²=1。
平面上有两点原点O(0, 0)和P(1, 2)，则向量OP = <1 – 0, 2 - 0> = <1, 2>向量OP方向的单位向量可以表示为：
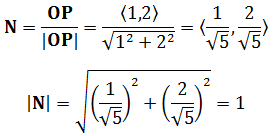
零向量
所有分量都为0的向量是零向量，零向量没有方向。
向量与直角坐标系
单位向量在平面直角坐标系的表示：
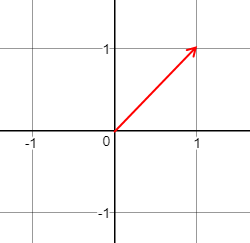
我们将原点称为标准位置，实际上单位向量的起点可以在任何位置，指向任何方向，只要满足模为1即可。
如果有一个向量a = (-1, 2)：
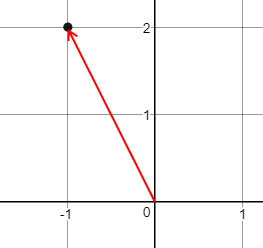
上图中向量的起点是原点，实际上(x1, x2)作为R2中的一个向量，可以是直角坐标系中的任意位置。如果以(-2,2)为起点，则a的终点是[-2,2]T + [-1, 2]T = [-3, 4]T如下图所示：
这都可以表示(-1,2)，可以说(-1,2)是一族向量，有无限多种表示法，它们的方向相同，模相等。为了简单起见，通常以原点作为向量的起点。
向量的加法和数乘
加法
向量的加法运算同矩阵的加法，我们需要理解的是矩阵加法在二维直角坐标系中系上的几何意义。
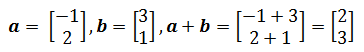
下面一组图都是a + b合法的表示：
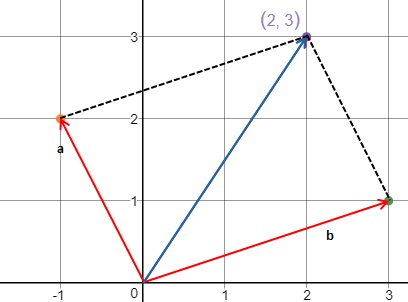
[0,0]T + a = [-1,2]T, [0,0]T + b = [3,1]T, a + b = [2,3] T
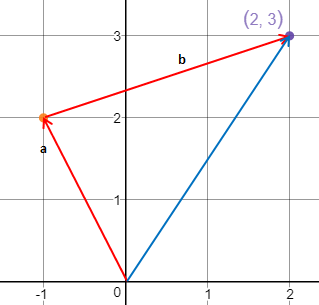
[0,0]T + a = [-1,2]T, [-1,2]T + b = [2,3]T, a + b = [2,3] T
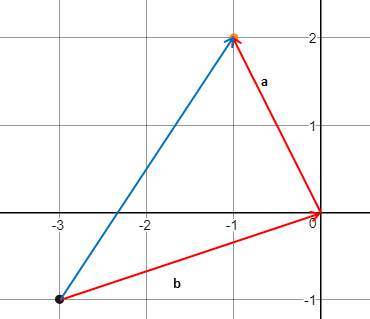
[0,0]T + a = [-1,2]T, [-3,-1]T + b = [0,0]T, a + b = [2,3] T
数乘
一个向量乘以一个标量：
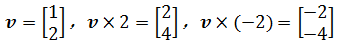
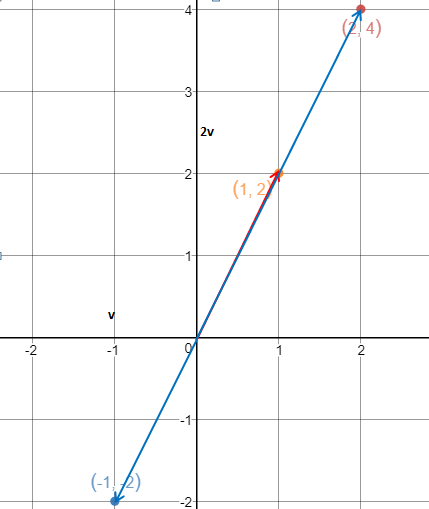
可以看到，向量的乘法其实是对原向量的伸缩；如果乘以正数，方向与原向量相同；乘以负数，方向与原向量相反。
减法
由向量的加法和数乘可知，x – y = x + (-1)×y，相当于先将y调转，再与x相加。
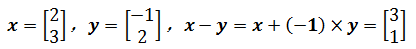
向量与方程组
方程组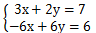 
可以看成
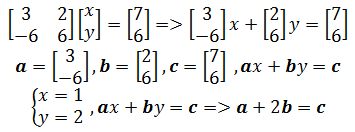
在坐标系中可以直观地展示该方程组：
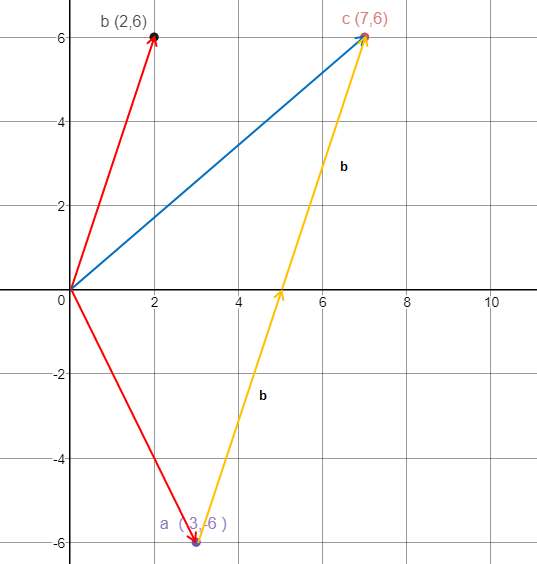
c = a + 2b
总结
- 向量，指具有大小和方向的量
- 单位向量是指模等于1的向量，一个单位向量的平面直角坐标系上的坐标表示可以是：(n,k) ，则有n²+k²=1
- 所有分量都为0的向量是零向量，零向量没有方向
- 向量的加法和数乘运算同矩阵运算，可扩展到任意纬度的向量
- 向量可以直观地展示线性方程组
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
