2017-2018-1 20155214 《信息安全系统设计基础》第3周学习总结
2017-2018-1 20155214 《信息安全系统设计基础》
第3周学习总结
教材学习内容总结
-
当x=2^n(n为非负整数),通过将n表示为(i+4j)的形式,可以把x转化为
首位为2^i,而后跟随j个0的16进制表示。 -
C语言对不同数据类型的数字范围设置了下界,但没有上界。
-
在JAVA中,单字节的数据类型称为Byte,而不是char,而且没有long long数据类型,这是为了保证无论在什么机器上,Java程序运行的表现都能完全一样。
教材学习中的问题和解决过程
-
问题1:有符号数与无符号数
-
问题1解决方案:
有符号数的计算机表示方式是补码,最高位为负权。而无符号数没有负权,为正值。
相同位值n的有符号与无符号数绝对值相加为2^n。
对有符号数和无符号数进行类型强转时,计算机位值不变。
当无符号加法运算下产生负值时,会进行模加运算。 -
问题2:如何理解IEEE浮点数中,
非规格化值的阶码值设置为(1-Bias)...这种方式提供了一种从非规格化值平滑转换到规格化值的方法。 -
问题2解决方案:
在2.4.3数字示例中,8位浮点格式,包含了4位阶码和3位小数位,其中偏置值Bias为[2^(4-1)-1]。

在规格化值中,阶码值为(e-7),e为阶码字段构成的无符号数。
而在非规格化值中,阶码值表示为(1-7),阶码字段为全0。
对于8位IEEE浮点格式而言,规格化值表示最小值为[0 0001 000],十进制表示为[2^(1-7)(0/8+1)]=(8/512)。
而非规格化值表示最大值[0 0000 111],十进制表示为[2^(1-7)(7/8)]=(7/512),与最小的规格化值相差为(1/512)。
若简单地将非规格化值的阶码值设置为(-Bias),则该十进制表示为[2^(-7)*(7/8)]=(7/1024),与最小的规格化值相差为(9/1024),
因此,将阶码值设置为(1-Bias),使得非规格化值与规格化值之间的差值缩小了,过渡更加平滑。
- 问题3:信息 = 位+上下文
- 问题3解决方案:
计算机中的数据以二进制按位储存,相同位的比特串在不同表示形式下代表着不同的含义。因此,当二进制比特串通过规定的格式排列后,就能表达出信息。
- 问题4:如何实现舍入
-问题4解决方案:
IEEE浮点格式定义了四种舍入,向偶数舍入,向零舍入,向下舍入,向上舍入。
向偶数舍入,只是简单的考虑最低有效数字是奇数还是偶数,即0舍1入。
-
目前采用的舍入规则遵循IEEE标准754的第4节,最贴近我们生活的就是Math.Round()函数。
-
输入
grep -k round | grep 3,试试

选择其中的round函数,man round
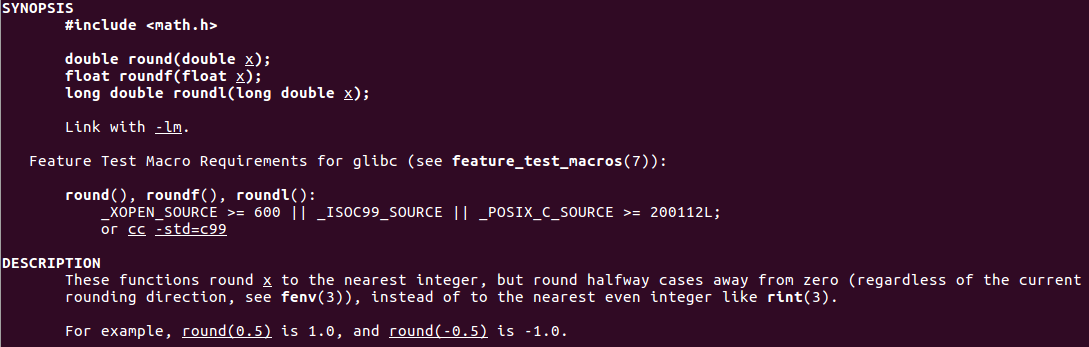

-
也就是说,round()的舍入方向参考fenv(),而非rint()的向偶舍入,那么分别搜索这两个函数试试看。
-

-
发现fenv()下的11个函数支持的是C99标准(1999年)。

-
nearbyint(), nearbyintf(), nearbyintl(), rint(), rintf(), rintl()则遵循IEEE-754标准(2008年),采用向偶数舍入。
-
尝试调用rint()。
源代码
1 #include <stdio.h>
2 #include <math.h>
3
4 int main()
5 {
6 float x;
7 double y;
8
9 x=1234567.89;
10 y=1234567.89;
11
12 printf("\n(float)x=%f,(double)y=%f\n",x,y);
13 printf("x=0x%d\n",*(int *)&x);
14 printf("rint(x)=%f\n",rint(x));
15
16 return 0;
17 }
- 输出结果

代码调试中的问题和解决过程
- 问题1:2.1.1中十进制和十六进制间的转换的perl脚本运行出现错误
bash: ./h2d: /usr/local/bin/perl: 解释器错误: 没有那个文件或目录

-
问题1解决方案:将脚本中
#!/usr/local/bin/perl改为#!/usr/bin/perl -
问题2:gcc编译时,显示
对rint未定义的引用

-
问题2解决方案:
-
需要提供数学库‘libm.a’

-
或者使用参数-lm也可以链接数学库
-
问题3:c语言中输出二进制时,若低32位为0,则输出0。
-
问题3解决方案:
在打印一个浮点数时,c将会实现:
一.浮点数转换成双精度 二. 打印低32位。
单精度浮点数,并非直接储存双精度IEEE浮点型表示。而是转换为双精度后,低位补零。然后输出低32位。
可以使用printf("%d\n",*(int *)&a);
-
Makefile的编写及实现
-
Makefile的作用
在linux下编写好Makefile文件后可以通过make命令进行自动化编译。 -
make的依赖性问题
首先make会在当前目录下寻找命名为“Makefile”的文件。如果找到,它会寻找文件中的第一个目标文件(target),并把这个文件作为最终的目标文件。
如果目标文件不存在,或者目标文件依赖的 .o 文件修改时间比它更新,make就会执行后面的命令来生成目标文件。
如果.o文件也不存在,那么make会在当前文件中寻找.o文件的依赖性文件,如果找到则生成.o文件。
如此,make会递归地去找文件之间的依赖关系,直到编译出第一个目标文件。 -
Makefile源代码
1 objects = main.o add.o sub.o mul.o div.o
2
3 testmymath: $(objects)
4 gcc -o testmymath $(objects)
5 main.o: mymath.h
6 add.o: mymath.h
7 sub.o: mymath.h
8 mul.o: mymath.h
9 div.o: mymath.h
10
11 .PHONY:clean
12 clean:
13 rm $(objects)
~
- 运行截图

代码托管
-
git截图
(statistics.sh脚本的运行结果截图)
上周考试错题总结
- 错题1及原因,理解情况
- 错题2及原因,理解情况
- ...
结对及互评
本周结对学习情况
- [20155216](博客链接)
- 结对照片
- 结对学习内容
其他(感悟、思考等,可选)
关于《深入理解计算机系统》的学习不同于上学期的Java,代码量减少了但对代码的理解要求加深了许多。
不再是在像翻工具箱一样,寻找称手的代码来组装程序。而是更要求理解如何实现,并且理解为何这样规定计算机。
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)

