Google的PageRank及其Map-reduce应用（日志五）

上一篇：Hadoop的安装（日志四）

 

1，算法的原理解释：

     如下图所示，G就是传说中的谷歌矩阵，这个矩阵是n*n型号的，n表示共计有n个网页。

     如矩阵中所示：

          11位置处的元素，是表示第一个网页指向的第一个网页的比例值。

          12元素，第二个网页指向第一个网页的比例值。

          所谓的比例值，这个名称是我给取的，意思就是指向的链接占据所有链接的比例，例如，1网页指向了2,3,4网页，那么其1指向2网页的比例值就为1/3。

     按照上面的原理，解析所有的链接，便得到了一个Google矩阵。

      Google论文中有：

           下面的公式之中α的取值范围是0在1之间任意取值，用于更加方便和精准的计算收敛的q。

           至于q=Gq,由于G本身是一个矩阵，所以这个公式其实就是一个线性变换的过程。初始的时候，q可以取任意的值，例如（1,1,1,1,1），但需要注意的是，其维数，一定是要和网页个数相同的。不断对q进行线性变换，最终变换得到的q会收敛于q,而这个就是q表示最终排名的向量。

      以上便是上面算法的所有原理解释。

2，例题（及其java实现）：

1)A网页有链接指向B,C,D,E

2)B网页有链接指向A,D

3)C网页有链接指向A,D

4)D网页有链接指向C

5)E网页有链接指向A,C

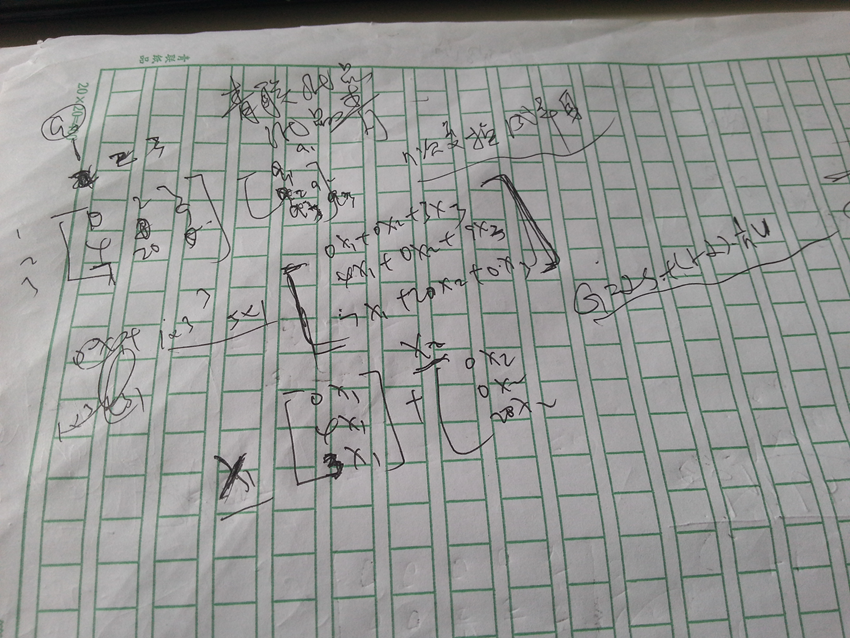
A 请写出这个网页链接结构的Google矩阵

B 手动或编程计算这5个页面的PR值

    Google矩阵：

   代码实现：这个代码实现，是本人一步步探索出来的，给出的注释比较详细，应该好理解，但其中还所许多需要优化的地方，看上去依旧很low b，请不要见怪哈。

                 主要原理，就是利用二维数组实现矩阵的运算，搞定了这个，一切就简单。

package com.cgtz.main;
  3 /**
* @author Administrator
*
*/public class HelloWorld {
     public static void main(String[] args) {
             //原始矩阵
             double[][] sMatrix=new double[][]{
                     {0,  0.5,  0.5,   0,  0.5},
                     {0.25 ,  0  ,  0  ,  0,   0},
                     {0.25 ,  0   , 0  ,  1,  0.5},
                     {0.25 ,  0.5,  0.5  ,0 ,  0},
                     {0.25  , 0  ,  0  ,  0 ,  0}
             };
             //单位矩阵
             double uMatrix[][]=new double[][]{
                     {1,  0,  0,   0,  0},
                     {0 ,  1  ,  0  ,  0,   0},
                     {0 ,  0   , 1  ,  0,  0},
                     {0 ,  0,  0  ,1 ,  0},
                     {0  , 0  ,  0  ,  0 ,  1}
             };
             double qMatrix[]=new double[]{
                     1,1,1,1,1
             };           
             double gMatrix[][]=new double[5][5];
             gMatrix=getGMatrix(sMatrix,uMatrix);
             printMatrix(gMatrix);
             double[] lastQMatrix=getLastQMatrix(gMatrix,  qMatrix);
             for (int i = 0; i < lastQMatrix.length; i++) {
                System.out.println(lastQMatrix[i]);
            }                         
     }
     //计数，可以调试时使用，也可以用来确定整个迭代的循环进行了多少次
    static int count=0;
    //整个方法，就是得出最后的排名向量，是一个核心的方法
    private static double[] getLastQMatrix(double[][] gMatrix, double[] qMatrix) {
    //每迭代一次，count的次数就加上一。
         count+=1;
    /**
      创建一个临时的数组，次数组的的长度和需要线性变换的向量的长度相同，此数组可以当成数学中的一个向量。
      整个temp向量的作用就是用来存放最原始的特征向量，以便与最终的向量进行比较
    */ 
        double[] temp=new double[qMatrix.length];
        //
        for (int i = 0; i < temp.length; i++) {
            temp[i]=qMatrix[i];
        }
        System.out.println("temp[1]---1:"+temp[0]);
    /**
       下面的嵌套的for循环，是用来q特征向量与G矩阵进行相乘，特征新的向量，需要说明的是，这里其实就是五维空间到五维空间的映射。
    */
        for (int i = 0; i < gMatrix.length; i++) {
            double newQ=0;
            for (int j = 0; j < qMatrix.length; j++) {
                double tempValue=gMatrix[i][j]*qMatrix[j];
                System.out.println("tempValue:"+tempValue);
                newQ+=tempValue;           
            }
            qMatrix[i]=newQ;
            System.out.println("----------------");
        }
    //打印出迭代一次之后得到新的排名向量
        System.out.println("第"+count+"次迭代得到的矩阵。。。");
        for (int s = 0; s < temp.length; s++) {         
            System.out.println("qMatrix---"+qMatrix[s]);
        }
          /**
            下面的运算，是求两个向量之间的距离，
            公式为：
 73       */
        double distace=0;
        double sDistance=0;
        System.out.println("temp.length:"+temp.length);
        System.out.println("temp[1]---2:"+temp[0]);
        for (int i = 0; i < temp.length; i++) {
            double x=temp[i]-qMatrix[i];
            double x2=java.lang.StrictMath.pow(x,2);
            sDistance+=x2;
        }
        distace=Math.sqrt(sDistance);
        System.out.println("第"+count+"次迭代sDistance:"+sDistance);
    //这里自己任意取一个合适的distance来确定多大距离时停止迭代
        if(distace<0.0001){
            for (int i = 0; i < temp.length; i++) {
                System.out.println(qMatrix[i]);
            }
            return qMatrix;         
        }else{ 
            getLastQMatrix(gMatrix,qMatrix);
        }
        return qMatrix;
    }
    public static void printMatrix(double[][] matrix){
         for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix.length; j++) {
                System.out.print(matrix[i][j]+"--");
            }
            System.out.println();       
         }
     }
     private static double[][] getGMatrix(double[][] sMatrix, double[][] uMatrix) {
         double gMatrix[][]=new double[5][5];
         for(int i=0;i<sMatrix.length;i++){
             for(int j=0;j<sMatrix.length;j++){
                 gMatrix[i][j]=(0.5)*sMatrix[i][j];             
             }           
         }
         for(int i=0;i<uMatrix.length;i++){
             for(int j=0;j<uMatrix.length;j++){
                 gMatrix[i][j]+=(0.5)*(0.2)*uMatrix[i][j];           
             }                       
         }           
        return gMatrix;

    }


}

 

 

计算的结果：

第14次迭代得到的矩阵。。。

qMatrix—2.8735992663233403E-5

qMatrix—4.620592012663504E-6

qMatrix—3.089895664396781E-5

qMatrix—1.604329405333448E-5

qMatrix—4.620592012663504E-6

由结果可知，c的网页的排名最高。

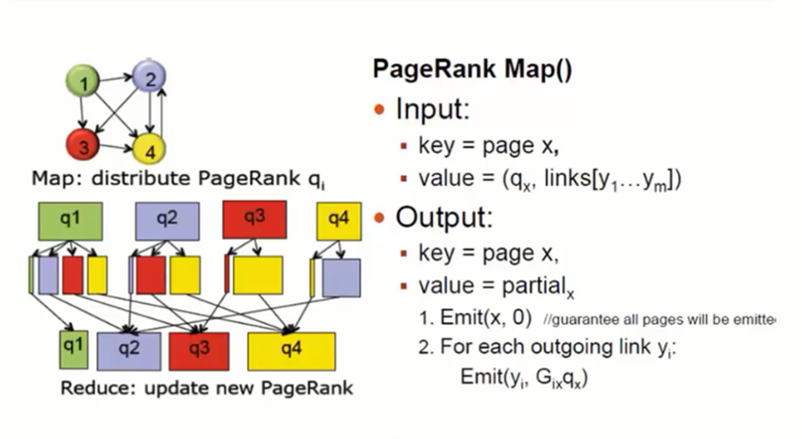
  3，当网页数量较多的时候，就使用分布式计算的方案：

原理见下面的图片：

每个网页乘以对应的分向量，而后变得到了新的q，即为变换之后的q

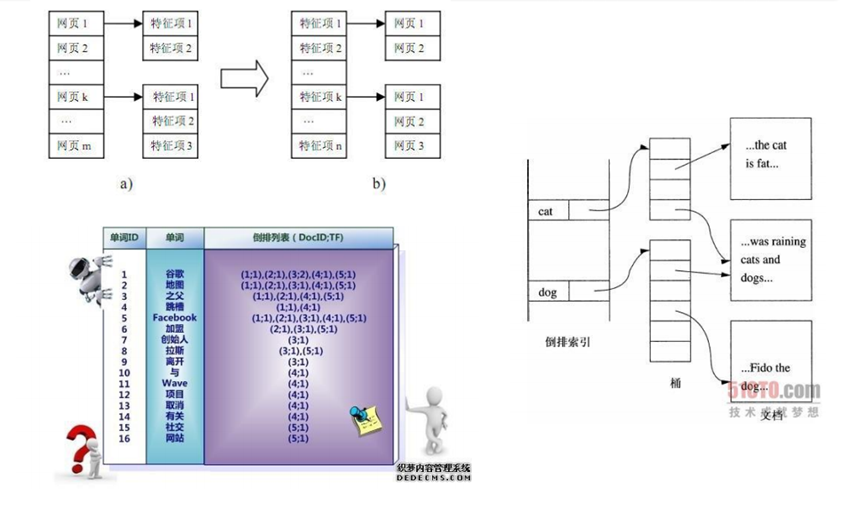
4,Google的分词技术：