数据挖掘之关联分析五(序列模式)
购物篮数据常常包含关于商品何时被顾客购买的时间信息,可以使用这种信息,将顾客在一段时间内的购物拼接成事务序列,这些事务通常基于时间或空间的先后次序。
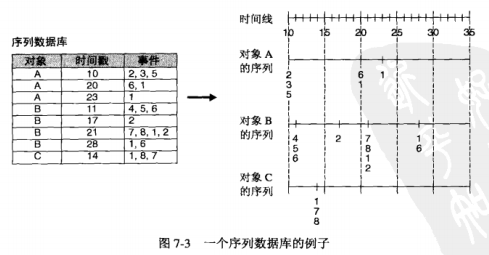
问题描述
一般地,序列是元素(element)的有序列表。可以记做\(s = (e_1, e_2, \cdots, e_n)\),其中每个\(e_j\)是多个事件的集簇,即\(e_j = {i_1, i_2, \cdots, i_k}\),如
- web站点访问者访问的web页面序列:
<{主页} {电子产品} {照相机和摄像机} {数码相机} {购物车} {订购确认} {返回购物}> - 计算机科学主修课程序列:
<{算法与数据结构, 操作系统引论} {数据库系统, 计算机体系结构} {计算机网络, 软件工程} {计算机图形学, 并行程序设计}>
序列可以用它的长度和出现时间个数刻画,序列的长度对应于出现序列中的元素个数,k-序列是包含k个事件的序列。上面例子中web序列包含7个元素和7个事件,课程序列包含4个元素和8个事件。
序列不但包括事件序列,也包括空间序列,如下面最后一行的DNA序列
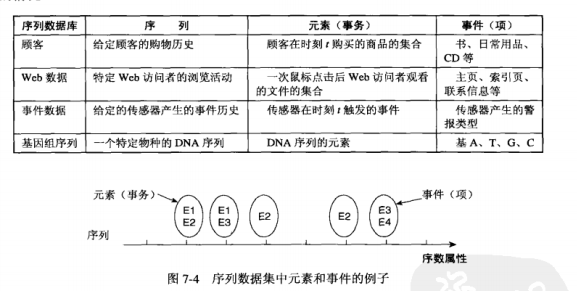
子序列subsequence
对于序列t和s,如果t中每个有序元素都是s中的一个有序元素的子集,那么t是s的子序列。形式化为,序列 $ t = < t_1, t_2, \cdots, t_m > $ 和 $ s = < s_1, s_2, \cdots, s_n > $,如果 $ 1 \leq j_1 \leq j_2 \leq \cdots \leq j_m \leq n $,使得 $ t_1 \subseteq s_{j_1}, t_2 \subseteq s_{j_2}, \cdots, t_m \subseteq s_{j_m} $,则t是s的子序列,并且t包含在s中。

序列模式发现
数据序列是指与单个对象相关联的时间的有序列表。设D为包含一个或多个序列的数据集。
序列s的支持度是包含s的所有数据序列所占的比例。如果序列s的支持度大于或等于用户指定的阈值minsup,则称s是一个序列模式(或频繁序列)
序列模式发现, 给定数据集D和用户指定的最小支持度阈值minsup,序列模式发现的任务是找出支持度大于或等于minsup的所有序列。
产生序列模式的一种蛮力方法是枚举所有可能的序列,并统计他们各自的支持度。
候选序列的个数比候选项集的个数大的多:
- 一个项在项集中最多出现一次,但是一个时间可以在序列中出现多次,如给定的两个项\(i_1\)和\(i_2\),能缠上一个候选2-项集\({i_1, i_2}\),但是可以产生许多候选2-序列,如\(<{i_1, i_2}>, <{i_1}, {i_2}>, <{i_2, i_1}>, <{i_1, i_1}>\)。
- 次序在序列中很重要,但是在项集中不重要。如{1, 2}和{2, 1}表示同一个项集,但是\(<{i_1}{i_2}>\)和$<{i_2}{i_1}> $表示不同序列。
先验原理Apriori对于序列数据成立

该算法迭代地产生新的候选k序列,减掉那些(k-1)序列非频繁的候选,然后对保留的候选计数,识别序列模式。
候选产生,一对频繁(k-1)序列合并,产生候选k-序列,为了避免重复产生候选,传统的Apriori算法仅当前k-1项相同时才合并一对频繁k-项集,序列也可以这样
序列合并过程:
序列\(s^{(1)}\)与另一个序列\(s^{(2)}\)合并,仅当从\(s^{(1)}\)中去掉第一个事件得到的子序列和从\(s^{(2)}\)中去掉最后一个事件得到的子序列相同,结果得到的候选是\(s^{(1)}\)与\(s^{(2)}\)的最后一个事件链接。\(s_{(2)}\)的最后一个事件可以作为最后一个事件合并到\(s_{(1)}\)的最后一个元素中,也可以起作为一个不同的元素,取决于下面条件
- 如果\(s_{(2)}\)的最后两个事件属于相同的元素,则\(s_{(2)}\)的最后一个事件在合并后的序列中是\(s_{(1)}\)的最后一个元素
- 如果\(s_{(2)}\)的最后两个事件属于不同的元素,则\(s_{(2)}\)的最后一个事件在合并后的序列中成为连接到\(s_{(1)}\)的尾部的单独元素。
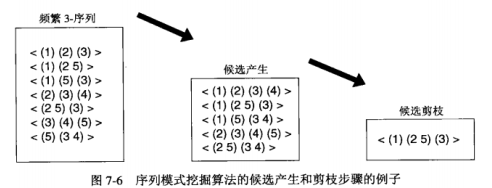
候选剪枝,如果候选k-序列至少有一个是你非频繁的,那么它将被减掉。
支持度计数,在支持度计数期间,算法将枚举属于特定数据序列的所有候选k-序列,这些候选的支持度将增值。计数之后,算法识别出频繁k-序列,并舍弃支持度小于阈值的候选。
时限约束
上面讨论的模式并没有再两个事件之间体现时限约束,即两个事件之间的间隔,因此需要定义新的序列模式。
序列模式的每个元素都与一个时间窗口\({l,u}\)相关联,其中\(l\)是该时间窗口事件的最早发生事件,而\(u\)是该时间窗口事件的最晚发生事件。
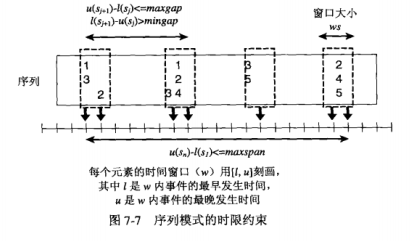
1.最大跨度约束
最大跨度约束指定整个序列中所允许的事件的最晚和最早发生时间的最大时间差。
一般地,最大时间跨度maxspan越长,在数据序列中检测到模式的可能性就比较大。然而较长的maxspan也可能捕获不真实的模式,因为增加这两个不相关的事件成为时间相关事件的可能性,此外,模式也可能涉及陈旧事件。
2.最小间隔和最大间隔约束
时限约束也可以通过限制序列中两个相继元素之间的时间差来指定,使用最大间隔约束的一个旁效就是可能违反先验原理。可能会出现序列中事件数增加时,支持度也增加,这就违背了先验原理。
邻接子序列, 序列s是序列 \(w = < e_1 e_2 \cdots e_k >\) 的邻接子序列必须满足下面条件之一,
- s是从\(w\)删除\(e_1\)或\(e_k\)中一个事件后得到
- s是从\(w\)删除至少包含两个事件的\(e_i\)中删除一个事件后得到
- s是t的邻接子序列,而t是w的邻接子序列

用邻接子序列概念,可以用如下方法修改先验原理,来处理最大间隔约束。
修订的先验原理, 如果一个k-序列是频繁的,则它的所有邻接k-1序列也一定是频繁的。
3.窗口大小约束
元素\(s_j\)中的事件不必同时出现,定义一个窗口大小阈值(ws)来指定序列模式的任意元素中最晚和最早出现之间的最大时间差,窗口为0表示统一元素中的所有事件必须同时出现。
下面例子中(ws=2,mingap=0, maxgap=3, maxspan=\(\infty\))

数据挖掘之关联分析一(基本概念)
数据挖掘之关联分析二(频繁项集的产生)
数据挖掘之关联分析三(规则的产生)
数据挖掘之关联分析四(连续属性处理)
数据挖掘之关联分析五(序列模式)
数据挖掘之关联分析六(子图模式)
数据挖掘之关联分析七(非频繁模式)




