时空权衡之输入增强 ----字符串匹配算法Horspool算法和Boyer-Moore算法

      在算法设计的时空权衡设计技术中，对问题的部分或者全部输入做预处理，对获得的额外信息进行存储，以加速后面问题的求解的思想，我们称作输入增强。

      其中字符串匹配算法Horspool算法和Boyer-Moore算法就是输入增强的例子。

      首先了解一下字符串匹配的概念。我们把在一个较长的n个字符的串中，寻找一个给定的m个字符的串的问题，称为字符串匹配问题。较长的串称为text，而需要寻找的串称为pattern。

      字符串匹配问题的蛮力算法很好理解：我们把pattern与text第一个字符对齐，从左往右比较pattern和text中的每一个字符，一旦匹配不成功，就把pattern往右移动一格，重新比较。最坏的情况需要比对n-m+1次（pattern不存在text中或者存在与text末尾），每次要进行m次比较，所以蛮力算法的最差性能是O(mn)。

      本次介绍的两个算法，都是想办法，在匹配出现不成功时，尽可能地移动更多的位置，从而实现算法性能的提升。

 

一．Horspool算法

 

      与KMP算法相反，这两个算法在比较pattern的时候，都是从右往左比较的。以下举一个例子。考虑我们要在某个text中查找“APPLE”这一pattern。

 

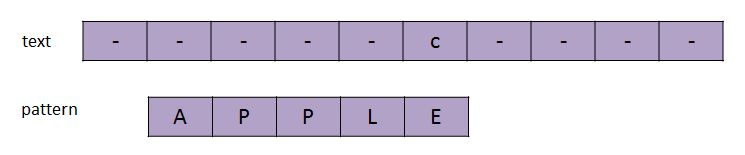
      从E开始，我们从右向左对比，如果pattern中所有的字符都匹配成功，则找到了一个子串。这时可以停止算法或者继续往右寻找。如果其中有字符匹配失败，我们需要把pattern往右移动。这里假设c是text中，对齐pattern最后一个字符的元素，则存在4种不同的情况。

      情况1，pattern中不包含c（这里的c是B）。直接移动pattern长的格数。

 

      情况2，pattern中包含c（这里的c是P），但c不是pattern中最后一个字符。则移动时应该把pattern中最右的c与text中的c对齐。

 

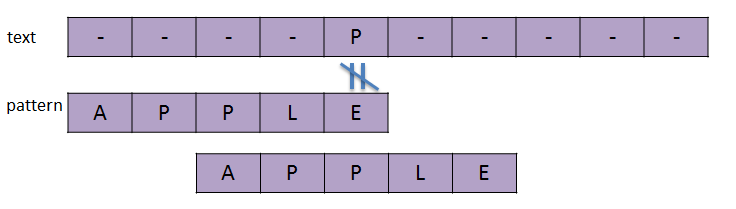
情况3，c正是pattern中最后一个字符（这里的c是E）。但剩余的m-1个字符中不包含c。也是直接移动pattern长的格数。

 

 

      情况4，c正是pattern中最后一个字符（这里的c是E）。但剩余的m-1和字符中也包含c。则类似情况2，把pattern中前m-1个字符中的c和text中的c对齐。

 

 

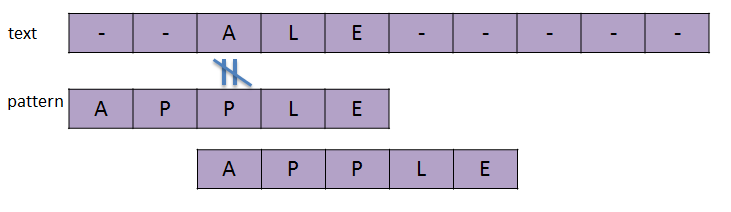
      为了加速算法，我们利用额外的空间来存储一个表。这个表中，对于text中的每一个字符，都对应一个值。这个值就是当pattern匹配不成功，且遇到的c是这个字符时，应当移动的距离。

      对于每一个字符c，我们用以下公式计算距离:

 

      例如，对于APPLE这字符串来说，除了A、P、L的单元格分别为4、2、1之外，表中所有得单元格都等于5（m=5）。这里E是5，而不是0。

 

      填表算法很简单，把所有单元格初始化为m，然后从左往右扫描pattern，对于pattern中第j个字符（0 ≤ j ≤ m-2），将它在表中的单元格改写为m-1-j。

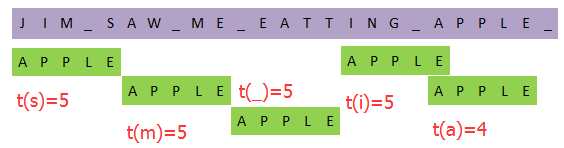
      加上一个完整的例子：

 

 

二．Boyer-Moore算法

      由于时间问题，下次继续更新。