算法导论第四章分治策略剖根问底(二)
在上一篇中,通过一个求连续子数组的最大和的例子讲解,想必我们已经大概了然了分治策略和递归式的含义,可能会比较模糊,知道但不能用语言清晰地描述出来。但没关系,我相信通过这篇博文,我们会比较清楚且容易地用自己的话来描述。
通过前面两章的学习,我们已经接触了两个例子:归并排序和子数组最大和。这两个例子都用到了分治策略,通过分析,我们可以得出分治策略的思想:顾名思义,分治是将一个原始问题分解成多个子问题,而子问题的形式和原问题一样,只是规模更小而已,通过子问题的求解,原问题也就自然出来了。总结一下,大致可以分为这样的三步:
分解:将原问题划分成形式相同的子问题,规模可以不等,对半或2/3对1/3的划分。
解决:对于子问题的解决,很明显,采用的是递归求解的方式,如果子问题足够小了,就停止递归,直接求解。
合并:将子问题的解合并成原问题的解。
这里引出了一个如何求解子问题的问题,显然是采用递归调用栈的方式。因此,递归式与分治法是紧密相连的,使用递归式可以很自然地刻画分治法的运行时间。所以,如果你要问我分治与递归的关系,我会这样回答:分治依托于递归,分治是一种思想,而递归是一种手段,递归式可以刻画分治算法的时间复杂度。所以就引入本章的重点:如何解递归式?
解递归式的三种方法
这里有三种方法:代入法、递归树法和主方法。(下面这一部分结合有些网友的总结和我的总结得来)
代入法:
定义:先猜测某个界的存在,再用数学归纳法去证明该猜测的正确性。
缺点:只能用于解的形式很容易猜的情形。
总结:这种方法需要经验的积累,可以通过转换为先前见过的类似递归式来求解。
递归树法:
起因:代换法有时很难得到一个正确的好的猜测值。
用途:画出一个递归树是一种得到好猜测的直接方法。
分析(重点):在递归树中,每一个结点都代表递归函数调用集合中一个子问题的代价。将递归树中每一层内的代价相加得到一个每层代价的集合,再将每层的代价相加得到递归式所有层次的总代价。
总结:递归树最适合用来产生好的猜测,然后用代换法加以验证。
递归树的方法非常直观,总的代价就是把所有层次的代价相加起来得到。但是分析这个总代价的规模却不是件很容易的事情,有时需要用到很多数学的知识。
主方法:
主方法是最好用的方法,书本上以”菜谱“来描述这种方法的好用之处,它可以瞬间估计一个递推式的算法复杂度。但是我们知道,这后面肯定是严格的数学证明在支撑着,对于我们用户来说,我们只用知道怎么用就行了。
优点:针对形如T(n) = af(n/b) + f(n)的递归式
缺点:并不能解所有上述形式的递归式,有一些特殊情况,见下文分析。
分析:三种情况,如下图,着重看圈线的部分:

直觉:看 f(n) 和 nlogba 的关系,谁大取谁,相等则两个相乘,但要注意看是否相差因子 nε。对于3),还要看是否满足条件 af(n/b) <= cf(n) .
就像上面所说的,该方法不能用于所有的形如上式的递归式,f(n)和nlogba的关系必须是多项式意义上的小于大于,即渐近关系(渐近小于、渐近大于),什么是渐近,就是两者相差一个因子nε。所以,在情况1和情况2之间有一定的间隙,同样情况2和请看3之间也有一定的间隙;对于情况3,还要看是否满足正则条件。
通过上面的讲述,我相信自己应该讲清楚了这三种方法,你也许还是有些困惑,但没关系,你只是缺乏例子的引导,下面我们就来看几个例子,其充分应用到了这三种方法。
代入法:(凭直觉、经验)
1)、习题4.3-1:T(n) = T(n-1) + n

2)、习题4.3-2:T(n) = T(n/2) + 1

递归树法:
1)、对递归式T(n) = 3T(n/2) +n,利用递归树确定一个好的渐近上界,用代入法进行验证。

2)、对递归式T(n) = T(n/2) + n2,利用递归树确定一个好的渐近上界,用代入法进行验证。

主方法:
1)、对于下列递归式,使用主方法求出渐近紧确界。
a、T(n) = 2T(n/4) + 1
b、T(n) = 2T(n/4) + n1/2
c、T(n) = 2T(n/4) + n
d、T(n) = 2T(n/4) + n2
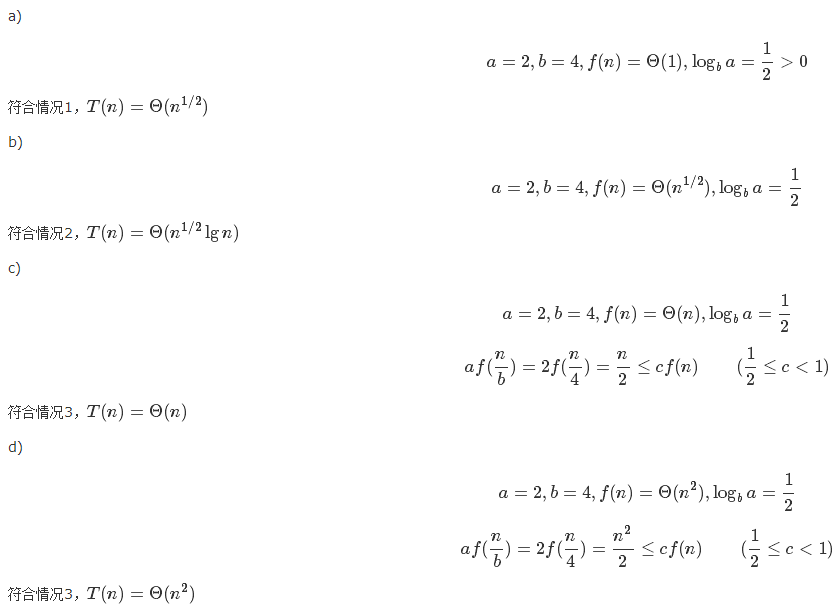
好了,以上只是热身用的,关于更多的课后习题的解答,请详见:http://www.cnblogs.com/Jiajun/archive/2013/05/08/3066979.html
我的公众号 「Linux云计算网络」(id: cloud_dev),号内有 10T 书籍和视频资源,后台回复 「1024」 即可领取,分享的内容包括但不限于 Linux、网络、云计算虚拟化、容器Docker、OpenStack、Kubernetes、工具、SDN、OVS、DPDK、Go、Python、C/C++编程技术等内容,欢迎大家关注。


