算法导论第四章分治策略实例解析(一)
一、第三章简单回顾
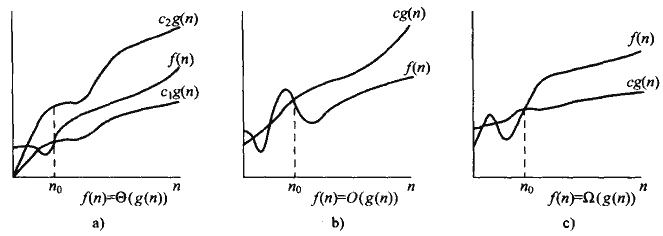
中间略过了第三章, 第三章主要是介绍如何从数学层面上科学地定义算法复杂度,以致于能够以一套公有的标准来分析算法。其中,我认为只要记住三个符号就可以了,其他的就看个人情况,除非你需要对一个算法剖根问底,不然还真用不到,我们只需有个印象,知道这玩意是用来分析算法性能的。三个量分别是:确定一个函数渐近上界的Ο符号,渐近下届Ω符号,以及渐近紧确界Θ符号,这是在分析一个算法的界限时常用的分析方法,具体的就详看书本了,对于我们更多关注上层算法的表达来说,这些显得不是那么重要,我的理解是Ο可以简单看成最坏运行时间,Ω是最好运行时间,Θ是平均运行时间。一般我们在写一个算法的运行时间时,大多是以Θ符号来表示。参考下面这幅经典的图:
二、第四章两大板块
第四章讲递归,也是数学的东西太多了,我准备这样来组织这章的结构:先用一个例子(最大子数组和)来讲解用到递归的一个经典方法——分治法,然后在引入如何解递归式,即引入解递归式的三种方法。
1、由分治法引发的
这一章提出了一个在现在各大IT公司在今天依然很喜欢考的一道笔试面试题:
求连续子数组的最大和 题目描述: 输入一个整形数组,数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)。 例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2, 因此输出为该子数组的和18。
要求时间复杂度是O(n),我们暂且不管这个,由浅入深地分析一下这道题,时间复杂度从O(n^2)->O(nlgn)->O(n)。
1)、第一,大部分人想到的肯定是暴力法,两个for循环,时间复杂度自然是O(n^2),如下:
1 /************************************************************************/ 2 /* 暴力法 3 /************************************************************************/ 4 void MaxSubArraySum_Force(int arr[], vector<int> &subarr, int len) 5 { 6 if (len == 0) 7 return; 8 int nMax = INT_MIN; 9 int low = 0, high = 0; 10 for (int i = 0; i < len; i ++) { 11 int nSum = 0; 12 for (int j = i; j < len; j ++) { 13 nSum += arr[j]; 14 if (nSum > nMax) { 15 nMax = nSum; 16 low = i; 17 high = j; 18 } 19 } 20 } 21 for (int i = low; i <= high; i ++) { 22 subarr.push_back(arr[i]); 23 } 24 }
2)、第二,看了《算法导论》,你可能会想到分治法,看完之后你肯定会为该分治思想而惊叹,尤其是“横跨中点”的计算思想。简单说下该分治思想,其实很简单,最大和子数组无非有三种情况:左边,右边,中间。
时间复杂度分析:
根据分治的思想,时间复杂度的计算包括三部分:两边+中间。由于分治的依托就是递归,我们可以写出下面的递推式(和合并排序的递推式是一样的):
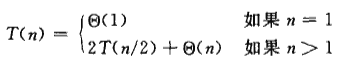
其中的Θ(n)为处理最大和在数组中间时的情况,经过计算(怎么计算的,请看本节第二部分:解分治法的三种方法),可以得到分治法的时间复杂度为Θ(nlgn)。代码如下:
1 /************************************************************************/ 2 /* 分治法 3 最大和子数组有三种情况: 4 1)A[1...mid] 5 2)A[mid+1...N] 6 3)A[i..mid..j] 7 /************************************************************************/ 8 //find max crossing left and right 9 int Find_Max_Crossing_Subarray(int arr[], int low, int mid, int high) 10 { 11 const int infinite = -9999; 12 int left_sum = infinite; 13 int right_sum = infinite; 14 15 int max_left = -1, max_right = -1; 16 17 int sum = 0; //from mid to left; 18 for (int i = mid; i >= low; i --) { 19 sum += arr[i]; 20 if (sum > left_sum) { 21 left_sum = sum; 22 max_left = i; 23 } 24 } 25 sum = 0; //from mid to right 26 for (int j = mid + 1; j <= high; j ++) { 27 sum += arr[j]; 28 if (sum > right_sum) { 29 right_sum = sum; 30 max_right = j; 31 } 32 } 33 return (left_sum + right_sum); 34 } 35 36 int Find_Maximum_Subarray(int arr[], int low, int high) 37 { 38 if (high == low) //only one element; 39 return arr[low]; 40 else { 41 int mid = (low + high)/2; 42 int leftSum = Find_Maximum_Subarray(arr, low, mid); 43 int rightSum = Find_Maximum_Subarray(arr, mid+1, high); 44 int crossSum = Find_Max_Crossing_Subarray(arr, low, mid, high); 45 46 if (leftSum >= rightSum && leftSum >= crossSum) 47 return leftSum; 48 else if (rightSum >= leftSum && rightSum >= crossSum) 49 return rightSum; 50 else 51 return crossSum; 52 } 53 }
3)、第三,看了《算法导论》习题4.1-5,你又有了另外一种思路:数组A[1...j+1]的最大和子数组,有两种情况:a) A[1...j]的最大和子数组; b) 某个A[i...j+1]的最大和子数组,假设你现在不知道动态规划,这种方法也许会让你眼前一亮,确实是这么回事,恩,看代码吧。时间复杂度不用想,肯定是O(n)。和暴力法比起来,我们的改动仅仅是用一个指针指向某个使和小于零的子数组的左区间(当和小于零时,区间向左减小,当和在增加时,区间向右增大)。因此,我们给这种方法取个名字叫区间法。
1 /************************************************************************/ 2 /* 区间法 3 求A[1...j+1]的最大和子数组,有两种情况: 4 1)A[1...j]的最大和子数组 5 2)某个A[i...j+1]的最大和子数组 6 /************************************************************************/ 7 void MaxSubArraySum_Greedy(int arr[], vector<int> &subarr, int len) 8 { 9 if (len == 0) 10 return; 11 int nMax = INT_MIN; 12 int low = 0, high = 0; 13 int cur = 0; //一个指针更新子数组的左区间 14 int nSum = 0; 15 for (int i = 0; i < len; i ++) { 16 nSum += arr[i]; 17 if (nSum > nMax) { 18 nMax = nSum; 19 low = cur; 20 high = i; 21 } 22 if (nSum < 0) { 23 cur = i + 1; 24 nSum = 0; 25 } 26 } 27 for (int i = low; i <= high; i ++) 28 subarr.push_back(arr[i]); 29 }
第四,你可能在平常的学习过程中,听说过该问题最经典的解是用动态规划来解,等你学习之后,你发现确实是这样,然后你又一次为之惊叹。动态规划算法最主要的是寻找递推关系式,大概思想是这样的:数组A[1...j+1]的最大和:要么是A[1...j]+A[j+1]的最大和,要么是A[j+1],据此,可以很容易写出其递推式为:
sum[i+1] = Max(sum[i] + A[i+1], A[i+1])
化简之后,其实就是比较sum[i] ?> 0(sum[i] + A[i+1] ?> A[i+1]),由此,就很容易写出代码如下:
1 /************************************************************************/ 2 /* 动态规划(对应着上面的贪心法看,略有不同) 3 求A[1...j+1]的最大和子数组,有两种情况: 4 1)A[1...j]+A[j+1]的最大和子数组 5 2)A[j+1] 6 dp递推式: 7 sum[j+1] = max(sum[j] + A[j+1], A[j+1]) 8 /************************************************************************/ 9 int MaxSubArraySum_dp(int arr[], int len) 10 { 11 if (len <= 0) 12 exit(-1); 13 int nMax = INT_MIN; 14 int sum = 0; 15 16 for (int i = 0; i < len; i ++) { 17 if (sum >= 0) 18 sum += arr[i]; 19 else 20 sum = arr[i]; 21 if (sum > nMax) 22 nMax = sum; 23 } 24 return nMax; 25 }
可以看出,区间法和动态规划有几分相似,我觉得两种方法的出发点和终点都是一致的,只不过过程不同。动态规划严格遵循递推式,而区间法是寻找使区间变化的标识,即和是否小于零,而这个标识正是动态规划采用的。
由于光这一部分就已经写得足够长了,为了方便阅读,所以本节第二部分:解递归式的三种方法 转 算法导论第四章编程实践(二)。
我的公众号 「Linux云计算网络」(id: cloud_dev),号内有 10T 书籍和视频资源,后台回复 「1024」 即可领取,分享的内容包括但不限于 Linux、网络、云计算虚拟化、容器Docker、OpenStack、Kubernetes、工具、SDN、OVS、DPDK、Go、Python、C/C++编程技术等内容,欢迎大家关注。


