【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
统计抽样的运用:抽取样本
作者 白宁超
2015年10月15日18:30:07
摘要:程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学,很多人认为是经济学或者数学的专利,与计算机并没有交集。诚然在传统学科中,其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及,统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书(偏向代码实现,需要读者有一定基础,可以参见后面PPT学习)。正如(吴军)先生在《数学之美》一书中阐述的,基于统计和数学模型对机器智能发挥重大的作用。诸如:语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要,因此,对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。( 本文原创,转载注明出处:统计抽样的运用:抽取样本 )
目录
【程序员眼中的统计学(1)】 信息图形化:第一印象
【程序员眼中的统计学(2)】集中趋势度量:分散性、变异性、强大的距
【程序员眼中的统计学(3)】概率计算:把握机会
【程序员眼中的统计学(4)】离散概率分布的运用:善用期望
【程序员眼中的统计学(5)】排列组合:排序、排位、排
【程序员眼中的统计学(6)】几何分布、二项分布及泊松分布:坚持离散
【程序员眼中的统计学(7)】正态分布的运用:正态之美
【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
【程序员眼中的统计学(9)】总体和样本的估计:进行预测
【程序员眼中的统计学(10)】假设检验的运用:研究证据
【程序员眼中的统计学(11)】卡方分布的应用
【程序员眼中的统计学(12)】相关与回归:我的线条如何?
1总体和样本
1.1总体和样本及相关概念
总体(population):统计学上指的是准备进行测量、研究或分析的整个群体。可以是人、得分,也可以是糖果 — 关键在于总体指的是所有对象。总体可分为有限总体和无限总体。
个体:组成总体的每一个考查对象。
样本(Sample):从总体中选取的一部分对象,是总体的一个子集。样本具有代表性,能在一定程度上反映总体特性。
抽样(Sampling):从总体中抽取部分个体的过程成为抽样,强调的是过程。
样本容量(Sample Size):样本中含有不同的个体数,该样本所包含的个体数即成为样本容量。也称为样本含量。
1.2 普查与样本调查
普查:指的是对总体进行研究或调查。一般用在人口、经济、农业等方面。但在实际的调查对象很大时,普查很难实现,基本都是用样本调查,就算我们经常听到的"全国人口普查",由于工作量大、难度大,在实际中是做不到的,所以不可能做到对全部的人口进行调查。
样本调查:仅对总体的一个样本进行的研究或调查称为样本调查。也常称为抽样调查。在书中的曼帝糖果实验中,一个口香糖样本就是所选取的一小部分糖球,而不是每一粒糖球。在多数情况下,进行样本调查比进行普查更切实可行,通常样本调查所费的时间和费用都较低,且不用考虑整个整体。
为方便大家更直观地了解普查和样本调查,下面列出两者之间的优缺点比较如表1所示:
|
普查 |
样本调查 |
|
|
优点 |
通过调查总体来收集数据,调查的结果准确 |
通过调查样本来收集数据,工作量较小,便于进行 |
|
缺点 |
工作量大,难度大,而且有些调查不宜使用普查 |
调查结果往往不如普查得到的结果准确 |
表1
1.3样本要有代表性
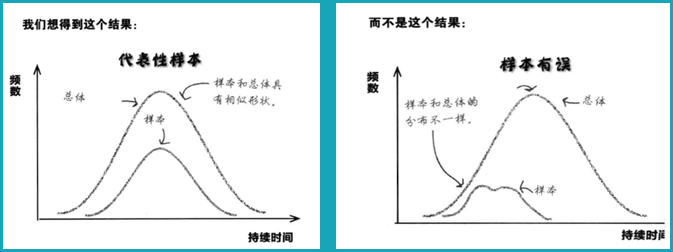
建立一个好样本的关键是尽量选择最符合总体的样本,即样本要具有代表性。如果样本具有代表性,则表示样本具有与总体十分相似的特性,进而意味着可以通过样本预测出总体具有哪种特性。
假定用一个具有代表性的口香糖球样本检验每种口香糖的口味持续时间,检验结果的分布可能如图1所示。我们知道,即使只是试吃了一个小样本的口香糖球,你也能对分布形状得出印象。试吃数量越多,图像形状越清晰。例如,通过查看抽样分布的形状,可以对总体分布的中心位置得出初步印象。
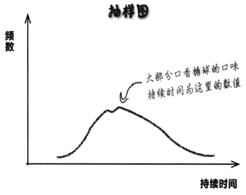

图1图2
对比总体分布图(图2),从两个图我们可以看出,尽管总体分布图代表所有的口香糖球,抽样分布图仅代表其中一些糖球,但二者的大致形状十分相似。它们具有一些共同的特点 — 例如数据中心的位置相同,这意味着可以用样本数据预测总体数据。
1.4 样本偏倚
1.4.1偏倚的定义
偏倚:在进行抽样时,调查者在无意间或者有意间带入样本的某种个人偏好就是偏倚。根据样本是否带有偏倚,可将样本分为无偏样本和偏倚样本。
无偏样本:无偏样本可以代表目标总体,即该样本与总体样本具有相似特性,我们可以利用这些相似特性对总体本身做出判断。样本无偏也就是样本具有代表性,能反映总体的特性。
偏倚样本:偏倚样本无法代表目标总体,由于样本与总体的特性不相似,无法根据样本对总体做出判断。如果我们试图用样本的分布形状预测总体的分布形状,最终会得出错误的结果。以曼帝糖果公司的口香糖球的持续时间为例(图3),带有偏倚的样本得出的持续时间与用总体得出的持续时间相差很大,所以偏倚的危害很大,它得出了错误的结果,不能帮助调查者作出决策或者作出错误的决策。
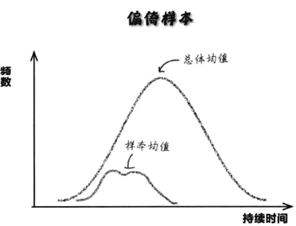
图 3
1.4.2 偏倚的来源
偏倚产生的原因有很多种,下面列出部分原因:
1、抽样空间中条目不齐全,因此未包含目标总体中的所有对象。如果条目不出现在抽样空间中,那么也不会出现在样本中。
2、抽样单位不正确。例如,也许抽样单位不应该是一粒粒的口香糖球,而是一盒盒的口香糖球。
3、为样本选取的一个个抽样单位未出现在实际样本中。例如,你可能发出一份调查问卷,但并不是人人都给出回应。
4、调查问卷的问题设计不当。设计的问题要中性,要适合每个人回答。例如,"曼帝糖果公司的糖果比其他品牌的糖果更可口,您同意吗?"这种提问带有偏倚,较好的做法是请受调查者自己说出他们偏爱的糖果品牌。
5、样本缺乏随机性。例如,如果在大街上展开调查,你可能会回避行色匆匆或气势汹汹的人,于是你就将气势汹汹的人或行色匆匆的人排除在调查范围之外了。
2 如何设计样本
样本的作用是用它判定总体情况。为了确保得到正确结果,需要明智地选择样本。让我们先来认清总体的实质,以便让样本尽量具有代表性,减少样本偏倚。那么,怎样设计样本呢?设计样本的具体步骤如下:
1 确定目标总体 :目标总体指的是你正在研究的、并且打算为其采集结果的群体。很大程度上取决于你的研究目的,比如说,你是打算收集世界上所有的口香糖的数据,还是收集某个特定品牌或者是某个特定类型的口香糖球的数据。
2 确定抽样单位 :一旦确定目标总体,就需要决定要抽取哪一类对象,通常,要抽取的对象类型就是在确定目标总体时所描述的对象类型,例如,可以是一粒口香糖球,也可以是一盒口香糖球。
3 确定抽样空间 :列出一张表,表中列出目标总体范围内的所有抽样单位,最好给每个抽样单位取个名或编个号,这张表就称为抽样空间。但是要注意,抽样空间不一定每次都能拟定,意思就是说,有时候不可能得出涵盖整个目标总体的抽样空间表。例如,如果要收集生活在某个地区的居民观点,由于人口流动,表中列举的名字就会受到影响;如果所处理的是一些相似的对象,例如口香糖球,那么为每一粒糖球命名或编号恐怕是不可能的,或者说是不现实的。 设计样本需要额外付出不少准备时间,但是,比起费时、费钱地对偏倚样本进行调查却换来一些错误结果,这要好多了。后者会让金钱和时间付诸东流,更有甚者,会有人根据错误的调查结果做出错误的决策。
3 如何选择样本
3.1 简单随机抽样
假设你有一个包含N个抽样单位的总体,需要选取包含n个抽样单位的样本。通过随机过程选取一个大小为n的样本就是简单随机抽样,简单随机抽样分为重复抽样和不重复抽样。
重复抽样:就是在选取一个抽样单位并记录下这个抽样单位的相关信息之后,再将这个单位放回总体中。这样做的结果是某个抽样单位有可能被选取一次。重复抽样常被称为放回抽样。
不重复抽样:不再将抽样单位放回总体。常被称为不放回抽样,我们在很多情况下用的是不放回抽样。
简单随机抽样调查是否合适,主要看是否满足:
(1)样本有代表性,
(2)样本容量要足够大,
(3)是否对每个个体都公平,每个个体是否都有可能成为调查对象 。
要让样本有代表性,以口香糖球为例,目标总体是曼帝糖果公司所有的各种颜色的口香糖球,抽取的样本就不能只有红色糖球,还要包含其他颜色的糖球,这样样本才具有代表性;如果我们抽取的样本数量很小,假设只抽取2粒糖球,那么得出的结果极有可能是不准确的,这里所说的样本数量"足够大",一般指n>30; 公平性很容易理解,如果不能保证每个个体被抽到的机会相等,那么抽到的样本也就不能很好地代表总体,不能准确地反映总体的特征。
简单随机抽样的特点:
(1)它要求被抽取样本的总体的个体数有限;
(2)它是从总体中逐个进行抽取;
(3)大多数情况下,它是一种不放回抽样;
(4)它是一种等概率抽样。
注意:简单随机抽样并不是随意或随便抽取,因为随意或随便抽取都会带有主观或客观的影响因素。
3.1.1抽签
3.1.1.1描述及步骤
抽签就是把抽样空间中的成员的名字或编号写在纸上或是球上,然后将其全部放入一个容器,均匀搅拌后,再随机取出n个名字或编号,以便得到足够的样本单位。
其主要步骤为:
(1)编号做签:将总体中的N个个体编上号,并把号码写到签上;
(2)抽签得样本:将做好的签放到容器中,搅拌均匀后,从中逐个抽出n个签,得到一个容量为n的样本.
概括为:编号、制签、搅匀、抽签、取个体
在抽签方法过程中,最关键的一步就是搅拌均匀。抽签法适用于当总体中所含的个体较少时。例如,从某班抽取5位同学去参加义务劳动,就可采用抽签的方法来抽取样本。
3.1.1.2 算法实现
基本描述:通过抽签的方式,从N个个体中抽取n个样本,抽签过程:编号、制签、搅匀、抽签、取个体,搅拌均匀用洗牌算法实现
应用场景:总体个数小,一般N<30适宜用抽签算法,例如从20名学生中随机抽取2名学生去义务劳动就可以用抽签算法,将20个学生的编号(0-19)作为ID和内容(这里用1-20表示)进行输入,循环调用getRandom()方法,每产生一个随机数cursor,就将下标为cursor的对象内容"cursor+1"添加到result结果集中,并且删除总体中的该元素,以保证不放回抽样规则,这样循环产生n个0-19范围的随机数,最后返回result结果集
算法优点:当总体个数小很适合,缺点就是总体个数大该算法不适用。算法使用的类型是Object通用类型,只要将总体中个体的类对象抽取出来进行输入就可以
算法输入参数:要抽取的样本大小n、以及Object数组total,即总体中的对象
算法中间结果:调用洗牌算法,将总体搅拌均匀后得到"新总体"total以及每一次循环产生的随机数cursor,这样利于取出Object类型的total数组下标为cursor的对象
代码:
package com.sunsheen.sampling; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class SimpleRandomSampling { /** 洗牌算法,实现抽签过程中将总体搅拌均匀的过程 * @author Linda * @param Object[] total,需要进行洗牌的数组的序号,相当于总体中每个个体的编号,输入参数就是总体中每个个体的编号数组total,数组中的对象是Object类型 * * **/ private static Object[] shuffleTotal(Object[] total){ //N指的是总体的长度,即总体个数 int N = total.length; for(int i=0;i<N;i++){ //调用Common类的getRandom方法,产生参数j,j就是要被交换对象的下标 int j = Common.getRandom(N); //实现total[i]与total[j]的交换,这里用temp作为中间临时变量,用来存储total[i]对象的内容 Object temp = total[i]; total[i]=total[j]; total[j]=temp; } //返回的是长度为N且搅拌均匀后的Object数组total return total; } /** draw抽签算法,不放回情况下,实现从总体total中逐个抽取n个样本,返回的是长度为n的数组result * * @param Object[] total,输入参数是搅拌均匀后的“新总体”数组total,数组中的对象是Object类型 * @param int n,输入参数是整型数n,即抽取样本的大小 * **/ public static Object[] draw(int n, Object[] total) { //创建长度为n的数组result,即返回的样本数组result int N = total.length; Object[] result = new Object[n]; Object[] shuffleTotal = shuffleTotal(total); //调用java中Arrays.asList方法,将total数组类型转化成List对象 List<Object> tempList = Arrays.asList(shuffleTotal); List<Object> totalList = new ArrayList<Object>(tempList); for(int i = 0;i <n ;i++){ int cursor = Common.getRandom(N);//调用Common类的getRandom方法,产生随机数cursor,即下标为cursor result[i] = totalList.get(cursor);//若存在,将下标为cursor的对象放入result样本数组,然后从总体中删除它,实现不重复(不放回)的抽样 totalList.remove(cursor); N = N - 1; } return result;//返回result数组 } public static void main(String[] args) { int N = 100; int n = 20; Object[] total = new Object[N]; Object[] sample = new Object[n]; for (int i = 0; i < N; i++) { total[i] = i+1; } sample = SimpleRandomSampling.draw(n, total); for (int i = 0; i < sample.length; i++) { System.out.println("编号:"+sample[i]); } } }
3.1.2 随机编号生成器
当总体中的个体较多时,即面对大型抽样空间时,"搅拌均匀"不容易做到,抽签不太可行,这样抽出的样本的代表性就会打折扣.此时,需要为抽样空间的每个成员编一个编号,再生成一组共n个随机编号,然后从该空间中取出边哈等于所生成的随机编号的成员。
tip:确保每个编号的生成机会相同,从而避免偏倚。
1.随机数表是统计工作者用计算机生成的随机数,并保证表中的每个位置上的数字是等可能出现的。
2.随机数表并不是唯一的,因此可以任选一个数作为开始,读数的方向可以向左,也可以向右、向上、向下等等。
3.用随机数表进行抽样的步骤:将总体中个体编号;选定开始的数字;获取样本号码。
4.由于随机数表是等概率的,因此利用随机数表抽取样本保证了被抽取个体的概率是相等的。
3.2 分层抽样
3.2.1描述及步骤
层(strata):将总体分割为几个相似的组,每个组具有类似的特性,这些特性或者组被称为层。
当总体是由有明显差异的几个部分组成时,可将总体按差异情况分成互不重叠的几个部分——层,然后按各层个体总数所占的比例来进行抽样,这种抽样叫做分层抽样(stratified sampling),也成为分类抽样。
先分层,再对每一个层进行简单随机抽样或系统抽样。
总体如何分层是分层抽样的一个重要问题。分层抽样中分多少层,要视具体情况而定。总的原则是:层内样本的差异要小,而层与层之间的差异尽可能地大,否则将失去分层的意义。举个例子在具体问题中如何分层,例如:要抽样了解某年参加高考考生的语文考试成绩,我们可以①按照科目分类:文科、理科、艺术、体育和外语五个层次。 ②按照地区分类:大城市、中等城市、城镇、乡镇四个层次。③按照学校分类:重点、非重点两个层次。
分层抽样的抽取步骤:
(1)总体与样本容量确定抽取的比例。
(2)由分层情况,确定各层抽取的样本数。
(3)各层的抽取数之和应等于样本容量。
(4)对于不能取整的数,求其近似值。
例:一个单位的职工有500人,其中不到35岁的有125人,35~49岁的有280人,50岁以上的有95人。为了了解该单位职工年龄与身体状况的有关指标,从中抽取100名职工作为样本,应该怎样抽取?
解:抽取人数与职工总数的比是100:500=1:5,则各年龄段(层)的职工人数依次是125:280:95=25:56:19,然后分别在各年龄段(层)运用简单随机抽样方法抽取。
所以,在分层抽样时,不到35岁、35~49岁、50岁以上的三个年龄段分别抽取25人、56人和19人。
3.2.2算法实现
基本描述:当总体是由明显差异的几个部分组成时,可将总体按差异情况分成互不重叠的几个部分—层,然后按各层个体总数所占的比例来进行抽样,这里分层的原则是:层与层之间差异足够大,而层内差异足够小。这里需要确定的是总体total和要抽取的样本大小n,根据自定义分层规则将总体分层,根据总体大小N(根据总体得到)和样本大小n确定抽取比例ratio=N/n,然后按层等比例抽取样本,从每一层抽取样本数为cn,将这cn个样本依次从该层中抽取出来,这样得到大小为各个层相加的个体总数n'的result结果集。
应用场景:分层抽样适用于总体个数较多且所有个体是有明显差异的几个部分组成,以书上内容为例,要评估曼帝糖果公司的糖果口味持续时间,糖果有几个不同颜色组成,不同颜色糖果的持续时间可能差异较大,这时就采用分层抽样;分层抽样应用很多,具体要根据总体的特征进行分析。不适用场景是分层规则不明显,这样分层后层与层之间差异小,这样用分层抽样意义不大,误差也相对较大。
算法适用的数据类型是Object通用类型,需要将总体中个体的类对象抽取出来进行输入。
优点:根据总体N和样本大小n确定比例,如果是整除,且根据比例从每层中抽取的个体数也是整数时误差最小;如果比例和最后从每层抽取的数都不能整除,误差最大;有一个不能整除误差位于两者之间。这里抽取样本直接取的是结果的整数部分,这样很可能实际抽取样本总数n'是小于计划抽取的样本数n,例如从总体为300的所有个体中按3:1抽取100个样本,总体中有3个层,每层有100个样本,这样按本算法计算就从3个层中分别抽取33、33、33个样本,实际抽取是99个样本,而计划抽取的是100个样本。
算法输入参数:要抽取的样本大小n、以及分好层的map对象数组total,total中的关键字key就是分层时的规则关键字,值就是具体对应key的每一个个体的内容,内容用Object类型存储,所以也适用于所有的Object对象,即总体中的对象数组。此算法的中间结果是从每一层抽取的样本数,用cn表示。
算法产生异常,如上所述,由于抽取比例和从每一层抽取的样本数都有可能是小数,所以会产生误差。本算法没有具体将ratio取整,而是在分层抽样过程中进行简单随机抽样时,对每一层的个体数L(当前层的长度)乘以n再除以N得到cn,这样减小了误差,但是这里还是取的整数部分,实际取的值cn是小于或者等于预计取的样本数,这样所有的层抽取的结果之和n'仍然是小于或者等于预计抽取的样本数n;如果这里采用四舍五入或者向上(下)取整的方法,这样的得结果实际抽取的样本数n'可能是小于、大于或者等于预计抽取的样本数n。具体怎样才能最小化误差,还需要进一步研究分析问题。
代码
package com.sunsheen.sampling; import java.util.ArrayList; import java.util.HashMap; import java.util.LinkedHashMap; import java.util.List; import java.util.Map; public class StratifiedSampling { /** * * @param n 要抽取的样本大小 * @param total 类型是map的总体的total * @return 大小为n的样本result */ public static Object[] stratified(int n, Map<Object, Object[]> total) { Object[] result = new Object[n]; List<Object> resultList = new ArrayList<Object>(); // 存放样本的List int N = 0; for (Object key : total.keySet()) { //根据total计算出总体大小N N = N + total.get(key).length; } for(Object key : total.keySet()){ //遍历map,将关键值为key(分层依据)的层放在currentGroup,对currentGroup进行按比例取样本 Object[] currentGroup = total.get(key); //这里不将n / N放在中间变量里,是为了减小误差,cn是存储每一层抽取的样本数 int cn = currentGroup.length * n / N; System.out.println(key+":"+cn); //调用简单随机抽样,从每一层随机抽取cn个样本 Object[] currentResult = SimpleRandomSampling.draw(cn, currentGroup); for (int i = 0; i < currentResult.length; i++) {//将每一层抽取的样本放到resultList中 resultList.add(currentResult[i]); } } result = resultList.toArray();//将resultList转化成数组result,并返回 return result; } public static void main(String[] args) { // 初始化数据 Map<Object, Object[]> total = new LinkedHashMap<Object, Object[]>(); int startNumber = 1; for (int i = 1; i < 4; i++) { Object[] classes = new Object[Common.getRandom(100,100)]; for (int j = 0; j < classes.length; j++) { classes[j] = "xs000" + (startNumber+j); } startNumber += classes.length; total.put("layer" + i, classes); } Object[] result = stratified(100, total); for (int i = 0; i < result.length; i++) { System.out.println((i+1)+":"+result[i]); } } }
3.3 整群抽样
3.3.1描述及步骤
总体中包含大量相似的组或群,就用整群抽样(cluster sampling),也称为聚类抽样。例如中秋月饼按盒出售,每一盒中的月饼的数量和口味组成都相似,于是每一盒月饼形成一个群。(以群为单位抽取)
确定特定群,对选定的几个群进行调查研究。
适用范围:无法进行其他方法的概率抽样;总体中的个体不明确
特点:群内个体之间差异大,群与群之间的差异小。这里需要与分层抽样对比起来,分层抽样是层与层之间的差异大,而层间差异小。
系统抽样的优点是易于实施,节省人力、物力;缺点就是群间差异大时,加大抽样误差,当群与群之间的差异大时,说明是不适合进行整群抽样的,而此时用整群抽样就会造成所得的样本不具有代表性,不能较好地放映总体的特性,就会造成误差。
3.3.2算法实现及说明
基本描述:将分好群的总体按群作为抽样单位,从总群数中用简单随机抽样抽取n个群,然后将这n个群的所有个体依次取出添加到resultList中,最后作为结果集返回。例如某年级平行班有10个,假设每班的人数差异不大,且平时成绩水平都差不多,要评估整个年级的某次成绩,就可以采用整群抽样对10个班进行简单随机抽取3个班,再将抽到班的所有学生编号和成绩(这里假设内容是学生的成绩)提取出来,存入到resultList中,最后返回resultList,即样本集。
应用场景:当总体个数较大且是由相似的群组成,这时可以用整群抽样。具体计算方法上面已写。
优点:总体个数较大时;当不知道某些群的所有个体只知道总体是由相似的群组成就可以用整群抽样,即事先不需要知道总体中所有个体的详细情况。缺点:当群与群之间的差异较大时,则不适合用整群抽样,而应该用分层抽样。算法的数据类型是map类型的数组total,即(key,value)键值对。
算法输入参数:要抽取的样本群数n以及分好群的map对象数组total,total中的关键字key就是分层时的规则关键字,值就是具体对应key的每一个个体的内容,内容用Object类型存储,所以也适用于所有的Object对象,即总体中的对象数组。该算法产生的中间结果是随机从总群数N随机抽取的样本群数n,要输出这些抽取的群
代码
package com.sunsheen.sampling; import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; public class ClusterSampling { /** * 整群抽样 * * @param total * @param n , 要抽取的群数 * * **/ public static Object[] cluster(int n, Map<Object, Object[]> total) { List<Object> resultList = new ArrayList<Object>(); // 存放样本的List Object[] resultClusterName = new Object[n]; // 要抽取的群的名称列表 Object[] clusterNames = new Object[total.size()]; // 总体的群标志列表 // 得到总体的所有群标志名称,存放到数组clusterNames中 int i = 0; for (Object clusterTag : total.keySet()) { clusterNames[i] = clusterTag; i = i + 1; } // 通过简单随机抽样获取要抽取的群的名称列表 resultClusterName = SimpleRandomSampling.draw(n, clusterNames); // 根据名称从总体中获取个体并存放到结果的列表中 for (int j = 0; j < n; j++) { System.out.println("Cluster:"+resultClusterName[j]); Object[] currentCluster = total.get(resultClusterName[j]); for (int k = 0; k < currentCluster.length; k++) { resultList.add(currentCluster[k]); } } // 将样本结果List转换成数组 Object[] result = resultList.toArray(); return result; } public static void main(String[] args) { //构造数据 Map<Object, Object[]> total = new HashMap<Object, Object[]>(); int startNumber = 1; for (int i = 1; i < 10; i++) { Object[] classes = new Object[Common.getRandom(20,30)]; for (int j = 0; j < classes.length; j++) { classes[j] = "xs000" + (startNumber+j); } startNumber += classes.length; total.put("Class" + i, classes); } Object[] result = cluster(4, total); for (int i = 0; i < result.length; i++) { System.out.println("Stu:"+result[i]); } } }
3.4系统抽样
3.4.1描述及步骤
系统抽样(systematic sampling):又称等距抽样或机械抽样,是指按照一定的顺序,机械地每隔K个单位抽取一个单位的抽样方法。其中k为一个特定数字。
从容量为N的总体中,用系统抽样抽取容量为n的样本,按照下面的步骤进行:
(1)采用随机的方式将总体中的个体编号;
(2)将整个的编号按一定的间隔(设为K)分段,当N/n(N为总体的个体数,n为样本容量)是整数时,k=N/n;当N/n不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数N'能被n整除,这时,k=N'/n,并将剩下的总体重新编号;
(3)在第一段中中简单随机抽样确定起始的个体编号l;
(4)将编号为l,l+k,l+2k,...,l+(n-1)k的个体抽出。
概括为:编号、分段、在第一段确定起始号、加间隔获取样本。
系统抽样的特点:
(1)用系统抽样抽取样本时,每个个体被抽到的可能性是相等的,个体被抽取到的概率等于N/n;
(2)系统抽样适用于总体中个体数较多时,抽取样本容量也较大时;
(3)系统抽样是不放回抽样
3.4.2算法实现及说明
基本描述:从容量为N的总体中,用系统抽样抽取容量为n的样本,按照下面的步骤进行:
(1)采用随机的方式将总体中的个体编号;
(2)将整个的编号按一定的间隔(设为K)分段,当N/n(N为总体的个体数,n为样本容量)是整数时,k=N/n;当N/n不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数N'能被n整除,这时,k=N'/n,并将剩下的总体重新编号;
(3)在第一段中中简单随机抽样确定起始的个体编号l;
(4)将编号为l,l+k,l+2k,...,l+(n-1)k的个体抽出。
概括为:编号、分段、在第一段确定起始号、加间隔获取样本
应用场景:总体个体数较大,总体不存在循环模式出现样本很适合,在零件质量检测经常用到。
不适用场景:总体中存在某种循环模式,样本会有偏倚。不适合用系统抽样
算法优点:快捷简单
缺点:总体中存在某种循环模式,样本会有偏倚。
算法输入参数:要抽取的样本大小n、以及Object数组total,即总体中的对象
中间结果:段数k、剔除的个数Y及在第一段要抽取的个体编号l,将N分成n段,每一段的个体数k=N/n以及余数Y=N%n,当Y不等于0时,需要从N个个体先剔除Y个个体再进行对n段进行等距抽样,先在第一段的编号1-k这个范围内进行简单随机抽样选取编号为l的个体,再间隔k进行抽取l+k、l+2k、…l+(n-1)k的编号个体取出。
异常 :未发生异常,需要理解一点,当分段不能整分时,先从N个个体先剔除Y个个体再将剩下的N-Y个总体进行重新编号分段。
代码
package com.sunsheen.sampling; import java.util.List; public class SystematicSampling { /** * 此方法功能就是从总体N中等距离抽取n个样本,若n能被N整除,则直接进行系统(等距)抽样,否则先剔除Y(N%n)个个体,再进行系统抽样 * @param n 要抽取的样本大小 * @param total 总体对象 * @return 大小为n的样本数组result */ public static Object[] systematic(int n, Object[] total) { //计算总体大小N int N = total.length; //创建返回的结果集 Object[] result = new Object[n]; //分别计算每段的个体数K和余数Y int k = N / n; int Y = N % n; List<Object> totalList = Common.arrayToList(total); if(Y != 0){//当总体n不能被N整除,则用简单随机抽样方法从N中剔除Y个个体 Object[] removeItem = SimpleRandomSampling.draw(Y, total); System.out.println("剔除的个体分别是:"); for (int i = 0; i < removeItem.length; i++) {//依次剔除,调用list的remove方法 totalList.remove(removeItem[i]); System.out.print(removeItem[i]+" "); } System.out.println(); System.out.println("--------------"); } //newTotal是存储要进行等距抽样的数组对象 Object[] newTotal = totalList.toArray(); //调用getRandom,得到从第一段抽取的随机编号为l的个体 int l = Common.getRandom(k); for (int i = 0; i < n; i++) {//for循环n次,即从每段间隔k抽取编号,依次得到编号为l、l+k、l+2k、...l+(n-1)K的个体 result[i] = newTotal[l + i*k]; System.out.println("抽取编号"+(l + i*k)+":"+result[i]); } return result;//返回result结果集 } public static void main(String[] args) { int N = 403; int n = 20; Object[] total = new Object[N]; Object[] sample = new Object[n]; for (int i = 0; i < N; i++) { total[i] = "xs000"+(i+1); } sample = systematic(n,total); for (int i = 0; i < n; i++) { //System.out.println("编号:"+sample[i]); } } }
4 总结与共享
4.1总结
4.1.1总体与样本相关概念
总体(population):指的是准备对其进行测量、研究或分析的整个全体。总体可分为有限总体和无限总体。
个体:组成总体的每一个考查对象。 样本(Sample):从总体中选取的一部分对象,代表总体的一个子集,样本具有代表性和广泛性。
抽样(Sampling):从总体中抽取部分个体的过程成为抽样,强调的是过程。
样本容量(Sample Size):样本中含有不同的个体数,该样本所包含的个体数即成为样本容量。也称为样本含量。
4.1.2普查与样本调查
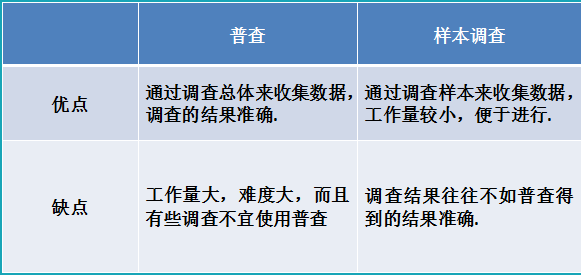
4.1.3抽样的比较
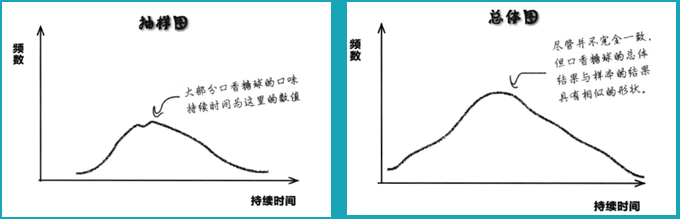
4.1.4几种抽样方法的比较

4.1.5非概率抽样
- 方便抽样(accidental sampling):指用最容易找到的人或物作为研究对象;优点是简便易行,缺点是样本的代表性差
- 配额抽样(quota sampling):是根据总体内有层次性的特点,利用总体内各层的构成比抽取与总体相似的样本
- 主观抽样(purposive sampling):指研究者依据自己的专业知识和经验以及对调查总体的了解,有意识选取研究对象
- 网络抽样(network sampling):利用社会网络的优势和朋友间具有共性的特点来进行抽样
4.2共享
PPT:http://yunpan.cn/cFMqh4WNkQSrG 访问密码 7c6b
开源代码:http://yunpan.cn/cFMPgkrBm4aCP 访问密码 a6a4
作者:白宁超,工学硕士,现工作于四川省计算机研究院,研究方向是自然语言处理和机器学习。曾参与国家自然基金项目和四川省科技支撑计划等多个省级项目。著有《自然语言处理理论与实战》一书。 自然语言处理与机器学习技术交流群号:436303759 。
出处:http://www.cnblogs.com/baiboy/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架