【程序员眼中的统计学(5)】排列组合:排序、排位、排
排列组合:排序、排位、排
作者 白宁超
2015年10月15日18:30:07
摘要:程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学,很多人认为是经济学或者数学的专利,与计算机并没有交集。诚然在传统学科中,其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及,统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书(偏向代码实现,需要读者有一定基础,可以参见后面PPT学习)。正如(吴军)先生在《数学之美》一书中阐述的,基于统计和数学模型对机器智能发挥重大的作用。诸如:语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要,因此,对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。( 本文原创,转载注明出处:排列组合:排序、排位、排 )
目录
【程序员眼中的统计学(1)】 信息图形化:第一印象
【程序员眼中的统计学(2)】集中趋势度量:分散性、变异性、强大的距
【程序员眼中的统计学(3)】概率计算:把握机会
【程序员眼中的统计学(4)】离散概率分布的运用:善用期望
【程序员眼中的统计学(5)】排列组合:排序、排位、排
【程序员眼中的统计学(6)】几何分布、二项分布及泊松分布:坚持离散
【程序员眼中的统计学(7)】正态分布的运用:正态之美
【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
【程序员眼中的统计学(9)】总体和样本的估计:进行预测
【程序员眼中的统计学(10)】假设检验的运用:研究证据
【程序员眼中的统计学(11)】卡方分布的应用
【程序员眼中的统计学(12)】相关与回归:我的线条如何?
0 问题

1 基本计数法则
1 分类加法计数原则
定义:若具有性质A的事件有m个,具有性质B的事件有n个,则具有性质A或性质B的事件有m+n个。
例子:事件A:a点到b点乘火车有3条线路。
事件B:a点到b点乘汽车有2条线路。
则a点到b点共有(2+3)=5条不同线路
解释说明:完成一件事,有n类方法。在第1类办法中有m1种不同的方法,在第2类方法中有m2种不同的方法,……,在第n类方法中有mn 种不同的方法,则完成这件事的不同方法共有:N=m1+m2+...+mn
注意点:各类方法相互独立的。
2 分步乘法计数原则
定义:若具有性质A的事件有m个,具有性质B的事件有n个,则具有性质A与性质B的事件有m*n个。
例子:事件A:a点到b点有3条不同的路径。
事件B:b点到c点有2条不同的路径。
则a点到b点共有3*2=6条不同的路径。
解释说明:完成一件事,需要分成n个步骤。做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步与mn种不同的方法,则完成这件事的不同方法共有:N=m1*m2*mn
注意点:各个步骤相互依存。
3 分类计数原理与分布计数原理相同点与不同点
- 相同点: 分类计数原理与分布计数原理都是涉及完成一件事的不同方法的种数问题。
- 不同点: 分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事。 分布计数原理与“分布”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成。
2 排列
1 排列描述
排列的定义
设 A={a1,a2,...,an}是n个不同元素的集合,m满足0≤m≤n。任取A中m个元素按顺序排成一列,称为从A中取m个的一个无重排列。
例子:

排列符号定义
从n个不同元素中,任取m个元素的所有排列的个数叫做从n个元素的排列数,用符号![]() 表示。
表示。
排列计算公式
选排列:当m<n时的排列称为选排列。选排列数公式:

全排列:当m=n时的排列称为全排列。全排列公式:
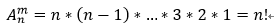
2 排列的优缺点
优点
可以辅助计算排列的概率问题。
缺点
此公式只适用m个元素是不同的情况,如果当m个元素有重复的时候就不能用此方法,使用受到条件限制。
排列应用
可以计算彩票的中奖概率,分析彩票的购买的排列情况,如七位数等。
3 圆周排列
1 圆周排列描述
圆周排列定义
从n个不同的数中不重复的取出m个沿一圆圈排列,称为一个圆周排列,表示为![]() 。
。
圆周排列符号定义
从n个不同的数中不重复的取出m个沿一圆圈排列,得到的排列数,符号表示为 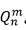 。
。
例子
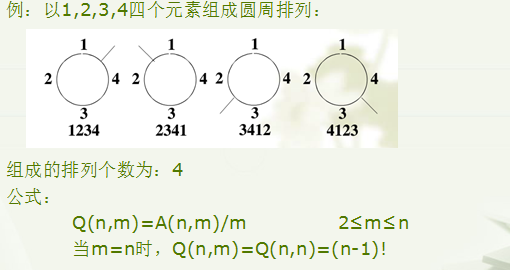
圆周排列计算公式

2 圆周排列优缺点
优点
可以快速计算圆周排列的排列数。
缺点
不区分圆周排列是逆时针还是顺时针排列。
圆周排列应用
在圆形的马场比赛跑道,可以计算赛马的中奖概率。
4 组合
1 组合描述
组合的定义
从n个不同元素中不重复的选取m个元素,组成一组(不管其顺序),称为从n个不同元素中选取m个元素的无重组合。
组合符号定义
从n个不同元素中不重复的选取m个元素,组成一组(不管其顺序),得到的排列数用符号 表示。
例子:

组合计算公式
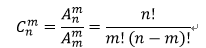
组合数的两个性质:  ,
,
2 组合的优缺点
优点
生活中经常计算概率的时候经常需要用到组合辅助计算。
缺点
输入的n个元素必须互不相同。
组合应用
可以计算彩票的中奖概率,分析彩票的购买的组合情况,如组合3。
5 排列组合算法
1 排列算法
递归法、字典序法、递增进位数制法、递减近位数制法、邻位交换法、n进制法……
递归算法
输入:{1,2,3}。输出:123,132,213,231,312,321
算法思想:第一位取1,对2,3全排列。第一位取2,对1,3全排列。第一位取3,对1,2全排列。
字典序法
算法思想:设p是集合{1、2、3、4……n}的一个全排列:p=p1p2.....pn
1、从排列的右端往左,找出第一个比右边数字小的数字序号j,也就是第一个顺序两位数。
2、从右端开始到j.找出第一个比pj大的数字pk。
3、交换pj,pk
4、对交换后的集合中p(j+1)......pn顺序逆转,也就是顺序排列。
2 排列算法描述
排列算法输入数据、输出结果
* @param object 输入可选元素
* @param m 选取m个数排列
* @param out 输出排列后的元素集
* @return 输出排列总数
类和方法描述
类名:Permutation.java
方法:
getCountByLine(Object[] object, long m)获取无重排列数目
getCountByCircle(Object[] object, int m)获取无重圆周排列数目
getAllPermutation(Object[] in, List<Object[]> out, int index)得到所有排列
java代码实现
/**
* 获取无重线排列总数目
* 描述:从n个元数中选取m个元数进行全排列,得出一共有多少种排法
* 公式:A(m,n)=m!/(n-m)!
* 优缺点:输入数据必须互不相同。求阶乘时,使用了for循环,避免了递归方法导致内存溢出的风险。
* (object数组中元素总数为n,从object数组中选出的m个数排列)
* @param object 输入可选元素
* @param m 选取m个数排列
* @return 输出排列总数
*/
public static BigInteger getCountByLine(Object[] object, long m) {
long n = object.length;
BigInteger result = MathUtils.factorial(n-m+1, n);//计算n-m+1到n的阶乘
return result;
}
/**
* 获取无重圆周排列数目
* 描述:从n个数中选取m个数进行圆周排列,获取一共有多少种排法
* 公式:Q(m,n)=A(m,n)/m=m!/(m*(n-m)!)
* 优缺点:输入数据必须互不相同。m定义了int类型,限制了计算范围。
* (object数组中元素总数为n,从object数组中选出的m个数圆周排列)
* @param object 输入可选元素
* @param m 选取m个数排列
* @return 输出排列总数
*/
public static BigInteger getCountByCircle(Object[] object, int m) {
int n = object.length;
BigInteger result = MathUtils.factorial(n-m+1, n).divide(BigInteger.valueOf(m));//计算n-m+1到n的阶乘除以m
return result;
}
/**
* 全排列(递归)
* 例:输入{1,2,3}输出{1,2,3}{1,3,2}{2,1,3}{2,3,1}{3,1,2}{3,2,1}
* 描述:输入一个数组,对数组中的所有元素进行全排列,把每种排列放入out集合中。
* 优缺点:输入数据必须互不相同。使用了递归的算法,当输入数据比较大时,会存在内存溢出的危险。
* @param in 输入数据
* @param out 输出数据
* @param index 默认为0
*/
public static void getAllPermutation(Object[] in, List<Object[]> out, int index) {
if(index == in.length-1) {
Object[] outTemp = in.clone();
out.add(outTemp);
}
for(int i=index; i<in.length; i++) {
swap(in,index,i);
getAllPermutation(in,out,index+1);//递归
swap(in,index,i);
}
}
/**
* 获取所有排列
* 例:输入{1,2,3}输出{1}{2}{3}{1,2}{2,1}{1,3}{3,1}{2,3}{3,2}{1,2,3}……
* 描述:输入一个数组,先从数组中选取一个数全排列,再选取两个两个数全排列,再选取三个数全排列,把所有的得到的排列放入out集合中。
* 优缺点:输入元素必须互不相同。
* @param in 输入数据
* @param out 输出数据
*/
public static void getSelectPermutaion(Object[] in, List<Object[]> out) {
List<Object[]> outTemp = new ArrayList<Object[]>();
for(int i=0; i<in.length; i++) {
Combination.getCombination(in, outTemp, i+1);//获取所有组合
}
for(int i=0; i<outTemp.size(); i++) {
getAllPermutation(outTemp.get(i), out, 0);//对每种组合进行全排列
}
}
/**
* 交换下标为i,j两个元素
* 描述:对object数组的i,j位置的元素进行交换
* @param object
* @param i
* @param j
*/
public static void swap(Object[] object, int i, int j) {
Object temp = object[i];
object[i] = object[j];
object[j] = temp;
}
排列算法异常和误差
输入数据时检查数据类型,输出的数据被转换成Object类型了。
适用或不适用场景
输入的元素是互不相同的,并且有序排列。可以据此分析彩票的中奖率,比如七位数。
3 组合算法描述
二进制法
算法思想:首先初始化,将数组前n个元素置1,表示第一个组合为前n个数。然后从左到右扫描数组元素值的“10”组合,找到第一个“10”组合后将其变为 “01”组合,同时将其左边的所有“1”全部移动到数组的最左端。当第一个“1”移动到数组的m-n的位置,即n个“1”全部移动到最右端时,就得到了最后一个组合。
组合算法输入数据、输出结果
* @param in 输入可选元素
* @param m 选取m个数排列
* @param out 输出组合后的元素集
* @return 返回组合后的数目
类和方法描述
类名:Combination.java
方法:
getCount(Object[] in, long m)获取组合数
getCombination(Object[] in, List<Object[]> out, int m)获取组合后的所有情况
java代码实现
/**
* 获取无重组合数目
* 描述:从n个数中选取m个元素组成一组,得到一共有多少种不同的组合
* 公式:C(m,n)=n!/(m!*(n-m)!)
* @param in 输入可选元素
* @param m 每次选m个
* @return 返回组合后的总数目
*/
public static BigInteger getCount(Object[] in, long m) {
long n = in.length;
BigInteger result = BigInteger.valueOf(1);
if(m<2/n) {//增加计算效率
result = MathUtils.factorial(n-m+1, n).divide(MathUtils.factorial(1, m));//计算公式
} else {
result = MathUtils.factorial(m+1, n).divide(MathUtils.factorial(1, n-m));//计算公式
}
return result;
}
/**
* 组合(二进制法)
* 例:输入{1,2,3}从中选2个的数组合。输出:{1,2}{1,3}{2,3}
* 描述:从输入的元素中,选m个元素组合,把所有的组合存在out中
* @param in 输入数组
* @param out 输出组合后的数组集
* @param m 取出m个数
*/
public static void getCombination(Object[] in, List<Object[]> out, int m) {
int n = in.length;
int[] array = new int[n];
for(int i=0; i<n; i++) {//初始化
if(i<m)
array[i] = 1;
else
array[i] = 0;
}
List<int[]> list = new ArrayList<int[]>();
boolean flag = true;
while(flag) {
int[] intTemp = array.clone();
list.add(intTemp);
for(int i=0; i<n-1; i++) {
if(array[i]==1 && array[i+1]==0) {
array[i]=0;//交换i,i+1的值
array[i+1]=1;
if(array[0]==0) {//把i位置左边的1都移到最左边
for(int k=0,j=0;k<i;k++) {
if(array[k]==1) {
array[j]=1;
array[k]=0;
j++;
}
}
}
break;
}
if(i==n-2) flag = false;
}
}
for(int i=0; i<list.size(); i++) {//把二进制中的1转换成对应的数组
Object[] objTemp = new Object[m];
for(int j=0,k=0;j<n;j++) {
if(list.get(i)[j]==1) {
objTemp[k] = in[j];
k++;
}
}
out.add(objTemp);
}
}
组合算法异常和误差
输入数据时检查数据类型,输入数据的可选范围是受限的。输出的数据为Object类型了,可以通过类型转换变为与输入数据一致的类型。
适用或不适用场景
输入的元素必须是互不相同的,并且属于抽取不放回的情况,抽出是无序的。可以据此分析彩票的中奖率,比如组合3。
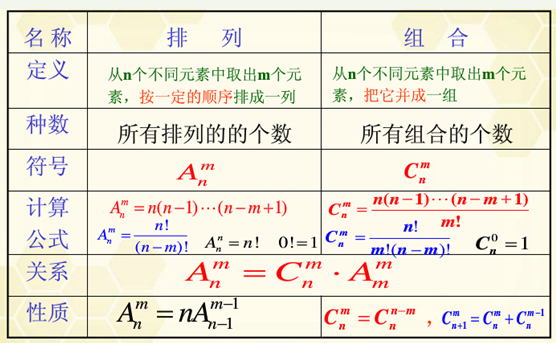
6 本章总结
排列与组合的区别
7 开源共享
PPT:http://yunpan.cn/cFwhKFiKraHWr 访问密码 5662
开源代码:http://yunpan.cn/cFwhjdaqB9iFs 访问密码 624d
作者:白宁超,工学硕士,现工作于四川省计算机研究院,研究方向是自然语言处理和机器学习。曾参与国家自然基金项目和四川省科技支撑计划等多个省级项目。著有《自然语言处理理论与实战》一书。 自然语言处理与机器学习技术交流群号:436303759 。
出处:http://www.cnblogs.com/baiboy/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架