【程序员眼中的统计学（12）】相关与回归：我的线条如何？

相关与回归：我的线条如何？

作者 白宁超
2015年10月25日22:16:07

摘要：程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学，很多人认为是经济学或者数学的专利，与计算机并没有交集。诚然在传统学科中，其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及，统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书（偏向代码实现，需要读者有一定基础，可以参见后面PPT学习）。正如（吴军）先生在《数学之美》一书中阐述的，基于统计和数学模型对机器智能发挥重大的作用。诸如：语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要，因此，对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。（ 本文原创，转载注明出处：相关与回归：我的线条如何？ )

1 算法的基本描述

1.1 算法描述

为了了解两个变量(自变量和因变量)之间的相关关系，利用线性回归法对二变量数据进行分析，得出最佳拟合线和相关系数，从而通过一个变量的值，估计推测另一个变量的值。

1.2 定义

假如有一个二变量数据分布如下：

X	x₁	x₂	x₃	x₄	……	x_n-2	x_n-1	x_n
Y	y₁	y₂	y₃	y₄	……	y_n-2	y_n-1	y_n

变量X与Y的取值一一对应且呈现线性相关的关系。

1.3 符号解释

X：表示自变量
Y：表示因变量
x_i：表示自变量的取值

y_i：表示因变量的取值

1.4 计算方法

1、假设最佳拟合线的方程为：y=ax+b

2、计算自变量X和因变量Y的均值：，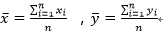

3、利用最小二乘法回归法求最佳拟合线的斜率：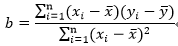

4、计算最佳拟合线的切距：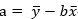

5、由求得的斜率和切距得出最佳拟合线的方程:

6、计算自变量X和因变量Y的标准差：，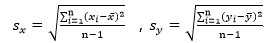

7、计算相关系数：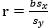

8、通过相关系数判断所求最佳拟合线与数据的拟合度，规则如下：

（1）如果相关系数的绝对值越接近1，则所求最佳拟合线的拟合度越高，可用于数据预测。

（2）如果相关系数的绝对值越接近0，则所求最佳拟合线的拟合度越低，不推荐用于进行预测（预测的结果可能不准确）。

2 算法的应用场景。

2.1 该场景下算法描述

案例描述：有一个不同场次的预计天晴时数和音乐会听众人数的关系数据样本，利用这些数据，如何基于音乐会当天预计天晴时数（小时）来估计出票情况。

2.2 该场景下算法定义

案例定义：有一个二变量数据同时给出预计天晴时数和音乐会听众人数，如下所示：

天晴时数（小时）	1.9	2.5	3.2	3.8	4.7	5.5	5.9	7.2
音乐会听众人数（百人）	22	33	30	42	38	39	42	55

如果音乐会当天预计天晴时数可能为4.3小时，请问音乐会听众人数可能会有多少人？

2.3 该场景下算法中符号解释

天晴时数：表示自变量

听众人数：表示因变量

2.4 该场景下算法计算方法

1、假设最佳拟合线的方程为：y=ax+b

2、计算天晴时数和听众人数的均值：

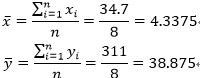
3、利用最小二乘法回归法求最佳拟合线的斜率：

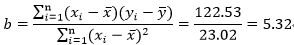
4、计算最佳拟合线的切距：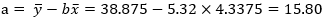

5、由求得的斜率和切距得出最佳拟合线的方程：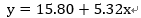

6、计算天晴时数和听众人数的标准差：

7、计算相关系数：

8、通过相关系数判断所求最佳拟合线与数据的拟合度并得出预测结果：

由于r接近1，说明音乐会听众人数和预计天晴时数之间有很强的正相关。换句话说，根据已有的数据，利用最佳拟合线根据预计天晴时数给出了期望音乐会听总人数的合理的良好估计。

当音乐会当天预计天晴时数可能为4.3小时，利用最佳拟合线方程，那么就可估计当天音乐会听众人数大约会是3868人。

3算法的优点和缺点

3.1 本算法优点

优点：发掘变量数据间的线性相关模式，并能为预测提出意见和结果。

3.2 本算法缺点

缺点：只适用于对已有的数据信息进行估计，不一定适用于数据限制以外的范围。以音乐会为例，当音乐会当天预计天晴时数可能为8小时，就不一定能良好估计听众人数可能会有多少人。

3.3 本算法适应场景

呈因果关系的变量之间，由原因因素值估计预测结果因素值。如光照时长与水稻产量。

3.4 本算法不适应场景

无因果关系的变量之间，例如，人的体重与身高。

3.5 本算法适用的数据类型

本算法适用于double数据类型，默认保留三位小数，可以自行设定保留位数。

4 算法的输入数据、中间结果以及输出结果

4.1 本算法输入数据

* @param twoVarData double[][[]，表示样本数据

* @param testiVar double，因变量测试值

* @param fraDigits int，结果保留几位小数

4.2 本算法中间结果

* @param iVarAvg double,表示自变量的均值

* @param dVarAvg double,表示因变量的均值

* @param slope double,表示最佳拟合线的斜率

* @param tangentDistance double,表示切距

* @param Sx double,表示自变量的标准差

* @param Sy double,表示因变量的标准差

4.3 本算法输出结果

* @return result String[4]，包含{斜率，切距，最佳拟合线方程，相关系数}结果字符型数值

* @return estValue double，因变量估计值

5 算法的代码参考

5.1 类和方法基本描述

类源码：见源程序：Statistics.src.CorrelationAndRegression

利用相关与回归原理计算二变量[自变量和因变量]数据的最佳拟合线，并通过最佳拟合线[y=a+bx]来挖掘二变量[自变量和因变量]数据之间的线性关系，从而通过自变量的值预测估计因变量的值。

5.2 类和方法调用接口

见源程序：Statistics.src.CorrelationAndRegression

CorrelationAndRegression.java 下包含如下方法：

calculateAvgValue(double[] varData,int fraDigits)//计算变量的均值

calculateSlope(double[][] twoVarData,int fraDigits) //计算最佳拟合线的斜率

calculateTangentDistance(double slope,double iVarAvg,double dVarAvg,int fraDigits) //计算最佳拟合线的切距

calculateStandardDeviation(double[] varData,int fraDigits)//计算变量的标准差

calculateCorrelationCoefficient(double slope,double Sx,double Sy,int fraDigits) //计算相关系数

calculateEstimatedValue(double slope,double tangentDistance,double testiVar,int fraDigits) //计算因变量的估计值

analyze(double[][] twoVarData,int fraDigits) //回归分析并得出结果

调用封装方法：Statistics.src.utils.ScoreUtil

ScoreUtil.java中的方法：

getFractionDigits(double, int) //对数值保留几位小数

5.3 源码

import utils.ScoreUtil;

/**
 * 相关与回归
 * @description 利用相关与回归原理计算二变量[自变量和因变量]数据的最佳拟合线，
 *     并通过最佳拟合线[y=a+bx]来挖掘二变量[自变量和因变量]数据之间的关系，从而通过自变量的值预测估计因变量的值。
 *     应用场景：例如，通过天气状态预测演唱会到场的人数；或者通过光照时长来估计植物的生长情况。
 *     局限性：只能根据已有的数据信息进行估计，不一定适用于数据限制意外的范围。
 *        例如，现有2000年到2010年的数据信息，就不能预测估计2010年以后的数据。
 * @author candymoon
 * @2015-8-13下午4:19:57
 */
public class CorrelationAndRegression {
    /**
     * 求变量值的平均值(公式：平均值=总和/总数)
     * @param varData 变量数据值
     * @param fraDigits 结果保留位数
     * @return 平均值
     */
    public static double calculateAvgValue(double[] varData,int fraDigits){
        double avgValue = 0;
        int  len = varData.length;//数组长度
        for (int i = 0; i < varData.length; i++) {
            avgValue += varData[i];
        }
        //计算均值
        avgValue = avgValue/len;
        //并将结果保留3位小数（四舍五入）
        String avgValue_String = ScoreUtil.getFractionDigits(avgValue, fraDigits);
        avgValue = Double.valueOf(avgValue_String);
        return avgValue;
    } 
    /**
     * 计算最佳拟合线(y=a+bx)的斜率b
     * @description 最佳拟合线(y=a+bx)的斜率b的计算公式为：b=∑((x-xAvg)(y-yAvg))/∑(x-xAvg)²
     * ,其中x为自变量，xAvg为自变量均值，y为因变量，yAvg为因变量均值。
     * @param twoVarData 二变量数据
     * @param fraDigits 结果保留位数
     * @return 斜率
     */
    public static double calculateSlope(double[][] twoVarData,int fraDigits){
        double slope = 0;//斜率
        double iVarAvg = 0;//自变量均值
        double dVarAvg = 0;//因变量均值
        //计算自变量均值和因变量均值
        iVarAvg = calculateAvgValue(twoVarData[0],fraDigits);
        dVarAvg = calculateAvgValue(twoVarData[1],fraDigits);
        int iVarLen = twoVarData[0].length;
        double numerator = 0;//分子 
        double denominator = 0;//分母
        //计算公式的分子和分母
        for (int i = 0; i < iVarLen; i++) {
            double x = twoVarData[0][i];
            double y = twoVarData[1][i];
            numerator += (x-iVarAvg)*(y-dVarAvg);
            denominator += (x-iVarAvg)*(x-iVarAvg);
        }
        //计算斜率
        slope = numerator/denominator;
        //并将结果保留几位小数（四舍五入）
        String slope_String = ScoreUtil.getFractionDigits(slope, fraDigits);
        slope = Double.valueOf(slope_String);
        return slope;
    }
    /**
     * 计算最佳拟合线(y=a+bx)的切距a
     * @description 因为最佳拟合线要经过点(自变量均值，因变量均值),所以其计算公式为：
     *              a=dVarAvg-b*iVarAvg
     * @param slope 斜率
     * @param iVarAvg 自变量
     * @param dVarAvg 因变量
     * @param fraDigits 结果保留位数
     * @return 切距
     */
    public static double calculateTangentDistance(double slope,double iVarAvg,double dVarAvg,int fraDigits){
        double tanDis = 0;//切距
        //计算切距
        tanDis = dVarAvg-(slope*iVarAvg);
        //并将结果保留3位小数（四舍五入）
        String tanDis_String = ScoreUtil.getFractionDigits(tanDis, fraDigits);
        tanDis = Double.valueOf(tanDis_String);
        return tanDis;
    }
    /**
     * 计算变量数据的标准差
     * @description 标准差计算公式为：标准差 =((var-varAvg)²/(n-1))^2
     * @param varData 变量数据
     * @param fraDigits 结果保留位数
     * @return 标准差
     */
    public static double calculateStandardDeviation(double[] varData,int fraDigits){
        double standardDev = 0;//标准差
        double varAvg = 0;//变量均值
        double denominator = 0;//分母
        //计算变量均值
        varAvg = calculateAvgValue(varData,fraDigits);
        int varDataLen = varData.length;
        for (int i = 0; i < varDataLen; i++) {
            double var = varData[i];
            denominator += (var-varAvg)*(var-varAvg);
        }
        //计算标准差
        standardDev = Math.pow(denominator/(varDataLen-1),0.5);
        //并将结果保留3位小数（四舍五入）
        String standardDev_String = ScoreUtil.getFractionDigits(standardDev, fraDigits);
        standardDev = Double.valueOf(standardDev_String);
        return standardDev;
    }
    /**
     * 计算相关系数
     * @description 相关系数表示最佳拟合线与二变量数据的拟合程度，相关系数计算公式为：r = (b*Sx)/Sy;
     *  r的取值范围为[-1,1]，当|r|越接近1，则表示拟合程度越高；当|r|越接近0，则表示拟合程度越低
     *  (1)当r=-1时，表示完全负相关;(2)当r=1时，表示完全正相关;(3)当r=0时，表示不相关。
     * @param slope 斜率
     * @param Sx 自变量的标准差
     * @param Sy 因变量的标准差
     * @param fraDigits 结果保留位数
     * @return 相关系数
     */
    public static double calculateCorrelationCoefficient(double slope,double Sx,double Sy,int fraDigits){
        double r = 0;//相关系数
        r = (slope*Sx)/Sy;
        //并将结果保留3位小数（四舍五入）
        String r_String = ScoreUtil.getFractionDigits(r, fraDigits);
        r = Double.valueOf(r_String);
        return r;
    }
    /**
     * 计算因变量的估计值
     * @description 利用最佳拟合线方程y=a+bx求解
     * @param slope 最佳拟合线的斜率
     * @param tangentDistance 最佳拟合线的切距
     * @param testiVar 测试自变量值
     * @param fraDigits 结果保留几位小数
     * @return 因变量的估计值
     */
    public static double calculateEstimatedValue(double slope,double tangentDistance,double testiVar,int fraDigits){
        double estValue = 0;//估计值
        //利用最佳拟合线方程y=a+bx求解
        estValue = tangentDistance+(slope*testiVar);
        //并将结果保留3位小数（四舍五入）
        String estValue_String = ScoreUtil.getFractionDigits(estValue, fraDigits);
        estValue = Double.valueOf(estValue_String);
        return estValue;
    }
    /**
     * 求斜率、切距、最佳拟合线、相关系数
     * @param twoVarData 二变量数据
     * @param testiVar 测试值
     * @param fraDigits 结果保留几位小数
     * @return 字符串结果数组{斜率、切距、最佳拟合线、相关系数}
     */
    public static String[] analyze(double[][] twoVarData,int fraDigits){
        String[] result = new String[4];//字符串结果数组
        String bestFittingLine = "";
        double iVarAvg = 0;//自变量均值
        double dVarAvg = 0;//因变量均值
        double b = 0;//斜率
        double a = 0;//切距
        double r = 0;//相关系数
        double Sx = 0;//自变量的标准差
        double Sy = 0;//因变量的标准差
        //计算自变量和因变量的均值
        iVarAvg = calculateAvgValue(twoVarData[0],fraDigits);
        dVarAvg = calculateAvgValue(twoVarData[1],fraDigits);
        //计算斜率
        b = calculateSlope(twoVarData,fraDigits);
        //计算切距
        a = calculateTangentDistance(b,iVarAvg,dVarAvg,fraDigits);
        //计算自变量和因变量的标准差
        Sx = calculateStandardDeviation(twoVarData[0],fraDigits);
        Sy = calculateStandardDeviation(twoVarData[1],fraDigits);
        //计算相关系数
        r = calculateCorrelationCoefficient(b,Sx,Sy,fraDigits);
        //组合最佳拟合线方程
        bestFittingLine = "y="+a+"+"+b+"x";
        //将结果加入到结果数组
        result[0]= b+"";
        result[1]= a+"";
        result[2]= bestFittingLine+"";
        result[3]= r+"";
        return result;
    }

    /**
     * @param args
     */
    public static void main(String[] args) {
        /*
         * iVar是independent variable(自变量)的缩写
         * dVar是dependent variable(因变量)的缩写
         */
         double[] iVar = {1.9,2.5,3.2,3.8,4.7,5.5,5.9,7.2};//自变量值
         double[] dVar = {22,33,30,42,38,49,42,55};//因变量值
         double[][] twoVarData = new double[][]{iVar,dVar};//二变量数据
         int fraDigits = 3;//结果保留几位小数数 
         double testiVar = 4.3;//测试自变量值
         String[] result = analyze(twoVarData,fraDigits);
         double estValue = 0;//估计值
         System.out.println("-------------输出结果---------------");
         System.out.println(" 斜率："+result[0]+" 切距："+result[1]);
         System.out.println(" 最佳拟合线："+result[2]);
         System.out.println(" 相关系数："+result[3]);
         estValue = calculateEstimatedValue(Double.valueOf(result[0]),Double.valueOf(result[1]),testiVar,fraDigits);
         System.out.println(" 测试自变量值："+testiVar);
         System.out.println(" 因变量估计值："+estValue);
         System.out.println("----------------------------------");
    }

}

6 共享

PPT:http://yunpan.cn/cFWAwExCtkmEd 访问密码 291e

开源代码：http://yunpan.cn/cFWAFPNrvn6PV 访问密码 8208

posted @ 2015-10-25 21:56 伏草惟存阅读(2002) 评论(2) 编辑收藏举报

刷新页面返回顶部