【Machine Learning】KNN算法虹膜图片识别

K-近邻算法虹膜图片识别实战

2017年1月3日18:26:33

摘要：随着机器学习和深度学习的热潮，各种图书层出不穷。然而多数是基础理论知识介绍，缺乏实现的深入理解。本系列文章是作者结合视频学习和书籍基础的笔记所得。本系列文章将采用理论结合实践方式编写。首先介绍机器学习和深度学习的范畴，然后介绍关于训练集、测试集等介绍。接着分别介绍机器学习常用算法，分别是监督学习之分类（决策树、临近取样、支持向量机、神经网络算法）监督学习之回归（线性回归、非线性回归）非监督学习（K-means聚类、Hierarchical聚类）。本文采用各个算法理论知识介绍，然后结合python具体实现源码和案例分析的方式（本文原创编著，转载注明出处:KNN算法虹膜图片识别实战(4)）

1 K-近邻算法（KNN, k-NearestNeighbor)

1.1 概念介绍

K-近邻算法(kNN，k-NearestNeighbor)分类算法由Cover和Hart在1968年首次提出。kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时，只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。在模式识别领域中，KNN是一种用于分类和回归的非参数统计方法。在如下两种情况下，输入包含特征空间中的k个最接近的训练样本。

在k-NN分类中，输出是一个分类族群。一个对象的分类是由其邻居的“多数表决”确定的，k个最近邻居（k为正整数，通常较小）中最常见的分类决定了赋予该对象的类别。若k = 1，则该对象的类别直接由最近的一个节点赋予。
在k-NN回归中，输出是该对象的属性值。该值是其k个最近邻居的值的平均值。

最近邻居法采用向量空间模型来分类，概念为相同类别的案例，彼此的相似度高，而可以借由计算与已知类别案例之相似度，来评估未知类别案例可能的分类。K-NN是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习。k-近邻算法是所有的机器学习算法中最简单的之一。无论是分类还是回归，衡量邻居的权重都非常有用，使较近邻居的权重比较远邻居的权重大。例如，一种常见的加权方案是给每个邻居权重赋值为1/ d，其中d是到邻居的距离。邻居都取自一组已经正确分类（在回归的情况下，指属性值正确）的对象。虽然没要求明确的训练步骤，但这也可以当作是此算法的一个训练样本集。k-近邻算法的缺点是对数据的局部结构非常敏感。本算法与K-平均算法（另一流行的机器学习技术）没有任何关系，请勿与之混淆。

1.2 举例分析一

我们提取电影的主要特征信息，特征选择：电影名称、打斗次数、接吻次数、电影类型。主要借助打斗和接吻特征判断电影属于那种类型（爱情片/动作片）.将采用KNN的方法进行模型训练，因为KNN属于有监督学习，因此设定一定规模的训练集进行模型训练，然后对测试数据进行分类预测，具体如图1所示：

图1 电影信息特征提取

假设我们选择6部电影作为训练集，将未知电影作为测试集，KNN预测未知电影属于什么类型？此时，纵坐标将视为特征维度，横坐标视为样本/样例维度。将电影名转化为矩阵数据表示如图2所示：

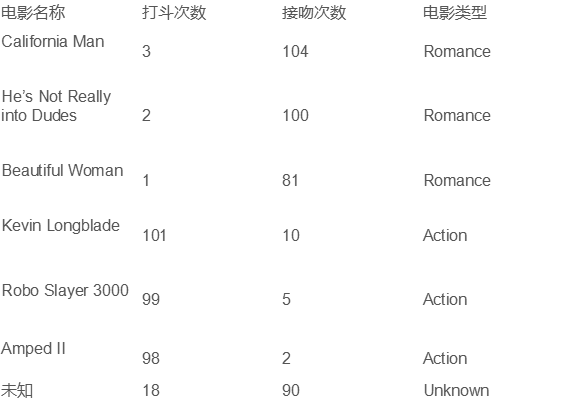
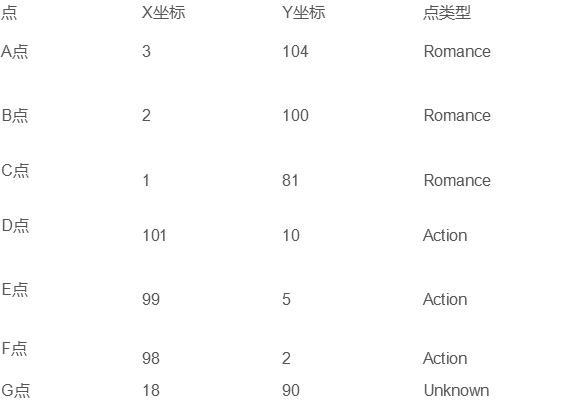
图2 电影信息特征转化

下面判断未知电影G点属于Romance或Action那种类型？不妨以图3形式化描述更好理解，假设黑色的豆子是动作片，绿色豆子是历史片，红色的豆子是爱情片。一部新电影G点到底属于哪个类型。主要判定G点周围的点属于哪个类型，至于G点周围如何设定，这就是K值的设置。K值不同直接影响分类结果，这个后续详细介绍。K的设定一般都是1,3,5,7,9等这样的奇数。其理由是因为采用少数服从多数的原理，不然设为偶数出现中立的情况就没有办法分类了。下图中绿色的原点周围大多属于绿豆，所以规为绿色豆子即【爱情片】。具体算法和代码后文介绍。

图3 KNN豆子分类示意图

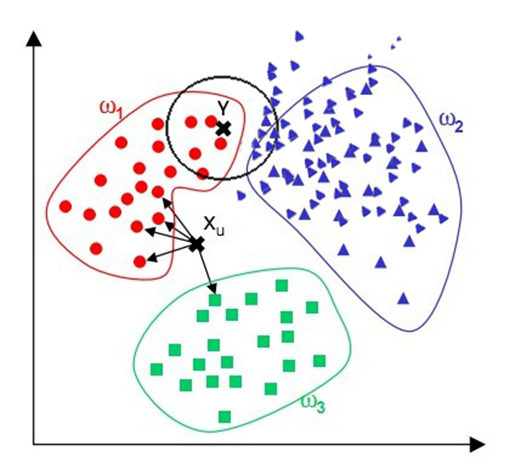
1.3 举例分析二

绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。如图4所示：

图4 K值的选择分类示意图

KNN算法的决策过程

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成反比。

训练样本是多维特征空间向量，其中每个训练样本带有一个类别标签。算法的训练阶段只包含存储的特征向量和训练样本的标签。在分类阶段，k是一个用户定义的常数。一个没有类别标签的向量（查询或测试点）将被归类为最接近该点的k个样本点中最频繁使用的一类。一般情况下，将欧氏距离作为距离度量，但是这是只适用于连续变量。在文本分类这种离散变量情况下，另一个度量——重叠度量（或海明距离）可以用来作为度量。例如对于基因表达微阵列数据，k-NN也与Pearson和Spearman相关系数结合起来使用。通常情况下，如果运用一些特殊的算法来计算度量的话，k近邻分类精度可显著提高，如运用大间隔最近邻居或者邻里成分分析法。

多数表决分类会在类别分布偏斜时出现缺陷。也就是说，出现频率较多的样本将会主导测试点的预测结果，因为他们比较大可能出现在测试点的K邻域而测试点的属性又是通过k邻域内的样本计算出来的。^[4]解决这个缺点的方法之一是在进行分类时将样本到k个近邻点的距离考虑进去。k近邻点中每一个的分类（对于回归问题来说，是数值）都乘以与测试点之间距离的成反比的权重。另一种克服偏斜的方式是通过数据表示形式的抽象。例如，在自组织映射（SOM）中，每个节点是相似的点的一个集群的代表（中心），而与它们在原始训练数据的密度无关。K-NN可以应用到SOM中。

2 K-近邻算法详述

2.1 算法步骤

准备数据，对数据进行预处理
选用合适的数据结构存储训练数据和测试元组
为了判断未知实例的类别，以所有已知类别的实例作为参照
选择参数K
维护一个大小为k的的按距离由大到小的优先级队列，用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组，分别计算测试元组到这k个元组的距离，将训练元组标号和距离存入优先级队列
遍历训练元组集，计算当前训练元组与测试元组的距离，将所得距离L 与优先级队列中的最大距离Lmax
进行比较。若L>=Lmax，则舍弃该元组，遍历下一个元组。若L < Lmax，删除优先级队列中最大距离的元组，将当前训练元组存入优先级队列。
计算未知实例与所有已知实例的距离
遍历完毕，计算优先级队列中k 个元组的多数类，并将其作为测试元组的类别。
根据少数服从多数的投票法则(majority-voting)，让未知实例归类为K个最邻近样本中最多数的类别
测试元组集测试完毕后计算误差率，继续设定不同的k值重新进行训练，最后取误差率最小的k 值。

2.2 距离的衡量方法:

Euclidean Distance 定义

其他距离衡量：余弦值（cos）, 相关度（correlation）, 曼哈顿距离（Manhattan distance）

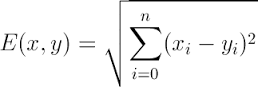
2.3 算法优缺点

当其样本分布不平衡时，比如其中一类样本过大（实例数量过多）占主导的时候，新的未知实例容易被归类为这个主导样本，因为这类样本实例的数量过大，但这个新的未知实例实际并木接近目标样本。如图5所示：

图5 KNN算法K值对分类影响示意图

算法优点：

简单、易于理解、容易实现
无需估计参数
无需训练
通过对K的选择可具备丢噪音数据的健壮性
适合对稀有事件进行分类
特别适合于多分类问题(multi-modal,对象具有多个类别标签)，kNN比SVM的表现要好

算法缺点：

当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。
需要大量空间储存所有已知实例
可理解性差，无法给出像决策树那样的规则
算法复杂度高（需要比较所有已知实例与要分类的实例）

算法改进：算法的改进方向主要分成了分类效率和分类效果两方面

分类效率：事先对样本属性进行约简，删除对分类结果影响较小的属性，快速的得出待分类样本的类别。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。
分类效果：采用权值的方法（和该样本距离小的邻居权值大）来改进，Han等人于2002年尝试利用贪心法，针对文件分类实做可调整权重的k最近邻居法WAkNN (weighted adjusted k nearest neighbor)，以促进分类效果；而Li等人于2004年提出由于不同分类的文件本身有数量上有差异，因此也应该依照训练集合中各种分类的文件数量，选取不同数目的最近邻居，来参与分类。[
考虑距离，根据距离加上权重。比如: 1/d (d: 距离）

参数选择

如何选择一个最佳的K值取决于数据。一般情况下，在分类时较大的K值能够减小噪声的影响，但会使类别之间的界限变得模糊。一个较好的K值能通过各种启发式技术（见超参数优化）来获取。噪声和非相关性特征的存在，或特征尺度与它们的重要性不一致会使K近邻算法的准确性严重降低。对于选取和缩放特征来改善分类已经作了很多研究。一个普遍的做法是利用进化算法优化功能扩展，还有一种较普遍的方法是利用训练样本的互信息进行选择特征。在二元（两类）分类问题中，选取k为奇数有助于避免两个分类平票的情形。在此问题下，选取最佳经验k值的方法是自助法。
属性
原始朴素的算法通过计算测试点到存储样本点的距离是比较容易实现的，但它属于计算密集型的，特别是当训练样本集变大时，计算量也会跟着增大。多年来，许多用来减少不必要距离评价的近邻搜索算法已经被提出来。使用一种合适的近邻搜索算法能使K近邻算法的计算变得简单许多。
近邻算法具有较强的一致性结果。随着数据趋于无限，算法保证错误率不会超过贝叶斯算法错误率的两倍[8]。对于一些K值，K近邻保证错误率不会超过贝叶斯的。
决策边界
近邻算法能用一种有效的方式隐含的计算决策边界。另外，它也可以显式的计算决策边界，以及有效率的这样做计算，使得计算复杂度是边界复杂度的函数。

3 K-近邻算法图片识别分类

3.1 KNN对虹膜图片分类处理

数据集介绍：数据集采集150条虹膜（如图6）数据的信息，横坐标为样例信息150条，纵坐标文特征信息（如图7）：萼片长度，萼片宽度，花瓣长度，花瓣宽度(sepal length, sepal width, petal length and petal width）类别（setosa,versicolor, virginica）.

我们设定2/3数据为训练数据，1/3数据为测试数据。首先采用python中sklearn机器学习工具包进行调用方法处理，然后自己写python进行完成KNN算法。

图6 虹膜花种类

图7 虹膜花特征

3.2 调用ython的机器学习库sklearn实现虹膜分类

下图8对应数据集：萼片长度，萼片宽度，花瓣长度，花瓣宽度，虹膜类别。数据集下载

图8 虹膜花部分特征数据

Python调用机器学习库scikit-learn的K临近算法，实现花瓣分类：

from sklearn import neighbors
from sklearn import datasets
'''
Description:python调用机器学习库scikit-learn的K临近算法，实现花瓣分类
Author:Bai Ningchao
DateTime:2017年1月3日15:07:25
Blog URL:http://www.cnblogs.com/baiboy/
Document：http://scikit-learn.org/stable/modules/neighbors.html
'''

knn=neighbors.KNeighborsClassifier()

iris=datasets.load_iris()

# print(iris)
'传入参数，data是花的特征数据，样本数据；target是分类的数据，归为哪类。'
knn.fit(iris.data,iris.target)

'knn预测分类,参数是 萼片和花瓣的长度和宽度'
predictedlabel = knn.predict([[0.1,0.2,0.3,0.4]])

print('分类结果[0:setosa][1:versicolor][2:virginica]：\n',predictedlabel,':setosa' if predictedlabel[0]==0 else 'versicolor or virginica')

运行结果如图9：

图9 虹膜花分类结果

3.3 KNN 实现Implementation

1 加载数据集,split划分数据集为训练集和测试集。

'加载数据集,split划分数据集为训练集和测试集'
def loadDataset(filename,split,trainingSet=[],testSet=[]):
    with open(filename,'r') as csvfile:
        lines = csv.reader(csvfile)
        dataset = list(lines)
        # print(dataset[:20])
        for x in range(len(dataset)-1):
            for y in range(4):
                dataset[x][y] = float(dataset[x][y])
            if random.random() < split:
                trainingSet.append(dataset[x])
                # print(dataset[x])
            else:
                testSet.append(dataset[x])
                # print('-->',dataset[x])

运行结果：

Train set: 104
Test set: 46

2 返回最近的K个近邻距离

'返回最近的K个label'
def getNeighbors(trainingSet,testInstance,k):
    distances = []
    length = len(testInstance)-1
    for x in range(len(trainingSet)):
        dist = euclideanDistance(testInstance, trainingSet[x], length)
        distances.append((trainingSet[x], dist))
    distances.sort(key=operator.itemgetter(1))
    neighbors = []
    for x in range(k):
        neighbors.append(distances[x][0])
        return neighbors

3 距离计算：

'计算距离'
def euclideanDistance(instance1,instance2,length):
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]),2)
    return math.sqrt(distance)

或者

import math
def ComputeEuclideanDistance(x1, y1, x2, y2):
    d = math.sqrt(math.pow((x1-x2), 2) + math.pow((y1-y2), 2))
    return d

d_ag = ComputeEuclideanDistance(3, 104, 18, 90)

print d_ag

4 根据投票进行分类划分'

'根据投票进行分类划分'
def getResponse(neighbors):
    classVotes = {}
    for x in range(len(neighbors)):
        response = neighbors[x][-1]
        if response in classVotes:
            classVotes[response] += 1
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(),key=operator.itemgetter(1),reverse=True)
    return sortedVotes[0][0]

预测结果（部分结果）：

>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-setosa', actual='Iris-setosa'
>predicted='Iris-versicolor', actual='Iris-versicolor'
>predicted='Iris-versicolor', actual='Iris-versicolor'
>predicted='Iris-versicolor', actual='Iris-versicolor'
>predicted='Iris-versicolor', actual='Iris-versicolor'
>predicted='Iris-versicolor', actual='Iris-versicolor'

测试数据结果预测：

5 计算准确率

'预测结果，算出精确度'
def getAccuracy(testSet, predictions):
    correct = 0
    for x in range(len(testSet)):
        if testSet[x][-1] == predictions[x]:
            correct += 1
    return (correct/float(len(testSet)))*100.0

训练集大小不同和K值设置不同对预测准确率性能影响如表1：

表1 虹膜花分类K值与训练数据集对准确率影响关系表

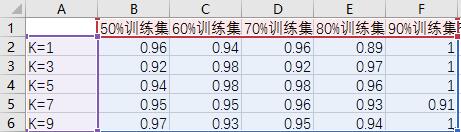
6 完整的KNN虹膜图片分类源码

import csv
import math
import random
import operator

'''
Description:python调用机器学习库scikit-learn的K临近算法，实现花瓣分类
Author:Bai Ningchao
DateTime:2017年1月3日15:07:25
Blog URL:http://www.cnblogs.com/baiboy/
Document：http://scikit-learn.org/stable/modules/neighbors.html
'''

'加载数据集,split划分数据集为训练集和测试集'
def loadDataset(filename,split,trainingSet=[],testSet=[]):
    with open(filename,'r') as csvfile:
        lines = csv.reader(csvfile)
        dataset = list(lines)
        # print(dataset[:20])
        for x in range(len(dataset)-1):
            for y in range(4):
                dataset[x][y] = float(dataset[x][y])
            if random.random() < split:
                trainingSet.append(dataset[x])
                # print(dataset[x])
            else:
                testSet.append(dataset[x])
                # print('-->',dataset[x])

'计算距离'
def euclideanDistance(instance1,instance2,length):
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]),2)
    return math.sqrt(distance)

'返回最近的K个label'
def getNeighbors(trainingSet,testInstance,k):
    distances = []
    length = len(testInstance)-1
    for x in range(len(trainingSet)):
        dist = euclideanDistance(testInstance, trainingSet[x], length)
        distances.append((trainingSet[x], dist))
    distances.sort(key=operator.itemgetter(1))
    neighbors = []
    for x in range(k):
        neighbors.append(distances[x][0])
        return neighbors

'根据投票进行分类划分'
def getResponse(neighbors):
    classVotes = {}
    for x in range(len(neighbors)):
        response = neighbors[x][-1]
        if response in classVotes:
            classVotes[response] += 1
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(),key=operator.itemgetter(1),reverse=True)
    return sortedVotes[0][0]

'预测结果，算出精确度'
def getAccuracy(testSet, predictions):
    correct = 0
    for x in range(len(testSet)):
        if testSet[x][-1] == predictions[x]:
            correct += 1
    return (correct/float(len(testSet)))*100.0




def main():
    trainingSet = []
    testSet = []
    split = 0.7 # 2/3训练集，1/3测试集
    loadDataset(r'../datafile/irisdata.txt',split,trainingSet,testSet)
    print('Train set: ' + repr(len(trainingSet)))
    print('Test set: ' + repr(len(testSet)))
  #generate predictions
    predictions = []
    k =5
    for x in range(len(testSet)):
        neighbors = getNeighbors(trainingSet, testSet[x], k)
        result = getResponse(neighbors)
        predictions.append(result)
        print ('>predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))
    print ('predictions: ' + repr(predictions))
    accuracy = getAccuracy(testSet,predictions)
    print('Accuracy: ' + repr(accuracy) + '%')


if __name__ == '__main__':
    main()

3.4 实验结果对比分析

折线图如图10所示：

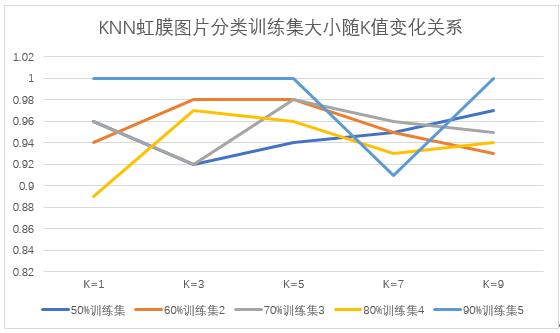
图10 折线图实验结果分析

条形图如图11所示：

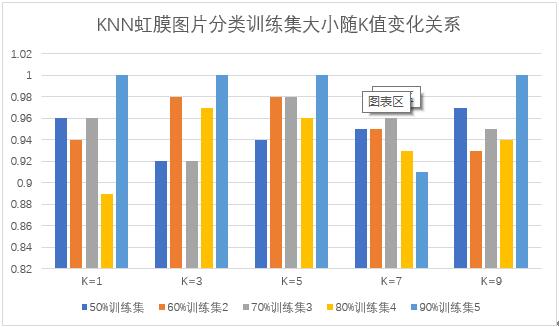
图11 条形图实验结果分析

实验结果：

上图结果表明，训练集的规模和K的取值，直接影响实验的分类性能。
当K值确定时，在K=1时候，分类效率最差，模型稳定性也差，随着训练集规模变化较为明显。当K=5和K=7时，训练集规模对模型影响相对稳定。综合比较K=5取得的平均准确率较高。
当训练集确定时，90%的训练集取得的实验效果最好，但是不稳定，70%训练集综合效果最好。

误差分析：