【NLP】揭秘马尔可夫模型神秘面纱系列文章（一）

初识马尔可夫和马尔可夫链

作者：白宁超

2016年7月10日20:34:20

摘要：最早接触马尔可夫模型的定义源于吴军先生《数学之美》一书，起初觉得深奥难懂且无什么用场。直到学习自然语言处理时，才真正使用到隐马尔可夫模型，并体会到此模型的妙用之处。马尔可夫模型在处理序列分类时具体强大的功能，诸如解决：词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取等。另外广泛应用于自然科学、工程技术、生物科技、公用事业、信道编码等多个领域。本文写作思路如下：第一篇对马尔可夫个人简介和马尔科夫链的介绍；第二篇介绍马尔可夫链（显马尔可夫模型）和隐马尔可夫模型以及隐马尔可夫模型的三大问题（似然度、编码、参数学习）；第三至五篇逐一介绍三大问题相关算法：（向前算法、维特比算法、向前向后算法）；最后非常得益于冯志伟先生自然语言处理教程一书，冯老研究自然语言几十余载，在此领域别有建树。（本文原创，转载注明出处：初识马尔可夫和马尔可夫链  )

目录

---

【自然语言处理：马尔可夫模型（一）】：初识马尔可夫和马尔可夫链

【自然语言处理：马尔可夫模型（二）】：马尔可夫模型与隐马尔可夫模型

【自然语言处理：马尔可夫模型（三）】：向前算法解决隐马尔可夫模型似然度问题

【自然语言处理：马尔可夫模型（四）】：维特比算法解决隐马尔可夫模型解码问题（中文句法标注）

【自然语言处理：马尔可夫模型（五）】：向前向后算法解决隐马尔可夫模型机器学习问题

1 马尔可夫个人简介

---

安德烈·马尔可夫，俄罗斯人，物理-数学博士，圣彼得堡科学院院士，彼得堡数学学派的代表人物，以数论和概率论方面的工作著称，他的主要著作有《概率演算》等。1878年，荣获金质奖章，1905年被授予功勋教授称号。马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面，他研究了连分数和二次不定式理论 ，解决了许多难题 。在概率论中，他发展了矩阵法，扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906～1912年间，提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现，一个系统的状态转换过程中第n次转换获得的状态常取决于前一次（第（n-1）次）试验的结果。马尔可夫进行深入研究后指出：对于一个系统，由一个状态转至另一个状态的转换过程中，存在着转移概率，并且这种转移概率可以依据其紧接的前一种状态推算出来，与该系统的原始状态和此次转移前的马尔可夫过程无关。马尔可夫链理论与方法在现代已经被广泛应用于自然科学、工程技术和公用事业中。

2 马尔可夫链

---

2.1  马尔科夫链的基本概念

序列分类器：序列分类器或序列标号器是给序列中的某个单元指派类或者标号的模型。马尔可夫模型（又叫显马尔可夫模型VMM）和隐马尔可夫模型（HMM）都是序列分类器。诸如：词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取都属于序列分类。

【随机过程的两层含义】

（1）    随机过程是一个时间函数，其随着时间变化而变化

（2）    随机过程的每个时刻上函数值是不确定的、随机的，即每个时刻上函数值按照一定的概率进行分布。

独立链：随机过程中各个语言符合或者词是独立的，不相互影响，则称这种链是独立链。反之，各语言词或者符号彼此有关则是非独立链。

等概率独立链与非等概率独立链：在独立链中，各个语言符合或者词是等概率出现的是等概率独立链，各个语言词或者语言符号是非等概率出现的则为非等概率链。

【马尔可夫链】

马尔可夫过程：在独立链中，前面语言符号对后面的语言符号无影响，是无记忆没有后效的随机过程，在已知当前状态下，过程的未来状态与它的过去状态无关，这种形式就是马尔可夫过程。

马尔可夫链：在随机过程中，每个语言符号的出现概率不相互独立，每个随机试验的当前状态依赖于此前状态，这种链就是马尔可夫链。

链的解析：也可以当做一种观察序列，诸如：“2016年是建党95周年”，就可以看着一个字符串链。其中如上字符串中每个字符出现是随机的，其他如果每个字出现是独立的就是独立链，如果每个字符出现有前面字符相关，即不独立具有依赖性则为马尔科夫链。

N元马尔科夫链：

考虑前一个语言符号对后一个语言符号出现概率的影响，这样得出的语言成分的链叫做一重马尔可夫链，也是二元语法。

考虑前两个语言符号对后一个语言符号出现概率的影响，这样得出的语言成分的链叫做二重马尔可夫链，也是三元语法。

考虑前三个语言符号对后一个语言符号出现概率的影响，这样得出的语言成分的链叫做三重马尔可夫链，也是四元语法。

类似的，考虑前（4,5，….,N-1）个语言符号对后一个语言符号出现概率的影响，这样得出的语言成分的链叫做（4,5，….,N-1）重马尔可夫链，也是（5，6，….,N）元语法。

马尔科夫链在数学上描述了自然语言句子的生成过程，是一个早期的自然语言形式的模型，后来N元语法的研究，都是建立在马尔科夫模型的基础上，马尔科夫链也就是显性的马尔科夫模型，马尔科夫链和隐马尔科夫模型都是有限自动机（状态集合状态之间的转移集）的扩充。

加权有限状态机：加权有限状态机中每个弧与一个概率有关，这个概率说明通过这个弧的可能性，且某一个点出发的弧具有归一化的性质，即某点出发的弧概率之和为1。

注意：马尔科夫链不能表示固有歧义的问题，当概率指派给没有歧义时，马尔科夫链才有用。

2.2  马尔可夫链描述

（1）    具有初始状态和终结状态的马尔科夫链描述如下：

（2）    没有初始状态和终结状态的马尔科夫链描述如下：

在一个一阶马尔可夫链中，我们假设一个特定的概率只与它前面一个状态有关，马尔可夫假设可以表示如下：

 

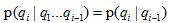
从一个状态i出发的所有弧的概率之和为1，即：

 

2.3        马尔可夫链应用实例

无初始状态和终结状态下，天气事件（1）hot hot hot hot 和（2）cold hot cold hot的马尔科夫链的序列概率：

   

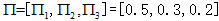
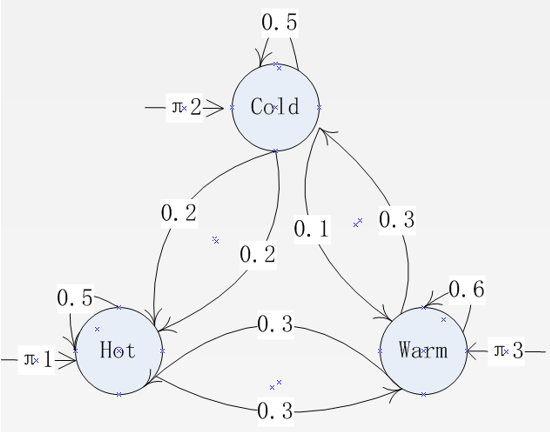
（1）  hot hot hot hot =0.5*0.5*0.5*0.5=0.0625

（2）  cold hot cold hot=0.3*0.2*0.2*0.2=0.0024

如上概率差别告诉我们用马尔科夫链编码实现世界天气事实是什么？天气事件的概率可以直接观察到。

 3 参考文献

---

【1】统计自然语言处理基础  Christopher.Manning等 著    宛春法等 译

【2】自然语言处理简明教程  冯志伟 著

【3】数学之美  吴军 著

【4】Viterbi算法分析文章  王亚强

声明：关于此文各个篇章，本人采取梳理扼要，顺畅通明的写作手法。一则参照相关资料二则根据自己理解进行梳理。避免冗杂不清，每篇文章读者可理清核心知识，再找相关文献系统阅读。另外，要学会举一反三，不要死盯着定义或者某个例子不放。诸如：此文章例子冰淇淋数量（观察值）与天气冷热（隐藏值）例子，读者不免问道此有何用？我们将冰淇淋数量换成中文文本或者语音（观察序列），将天气冷热换成英文文本或者语音文字（隐藏序列）。把这个问题解决了不就是解决了文本翻译、语音识别、自然语言理解等等。解决了自然语言的识别和理解，再应用到现在机器人或者其他设备中，不就达到实用和联系现实生活的目的了？本文原创，转载注明出处：初识马尔可夫和马尔可夫链