USACO-Shaping Regions

来源：http://www.nocow.cn/index.php/Translate:USACO/rect1

很明显灌水法是行不通的。

什么是灌水法？就是把每一个矩形都标记一遍，最后扫描整个大矩阵，算法的时间复杂度是O(N^2)，看数据规模就知道肯定死翘翘了。

这题我选用了漂浮法，也称碰撞法。

漂浮法在nocow上是这样描述的：

漂浮法

以逆序来进行放置，即n to 1。逆序的好处在于放置一个矩形后，俯视看到的就是最终俯视该矩形应该看到的。因为挡着它的矩形在之前已经放置好了，所以可直接统计，为递归创造了条件。每放一个矩形，可以想象成将其扔入一密度很大的海水底部，海分成了n层,然后矩形开始向上浮。在上浮过程中若碰撞到其他的矩形则断裂成几个小矩形，继续上浮，直到浮出水面。于是想到用个递归来模拟上浮过程。

下面是我的个人见解：

我们先考虑简单的情况：

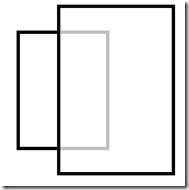
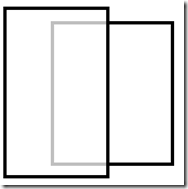
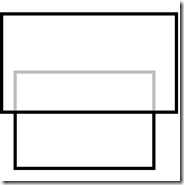
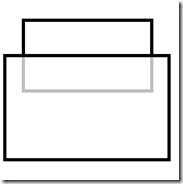
         情况1                               情况2                                    情况3                                   情况4

     

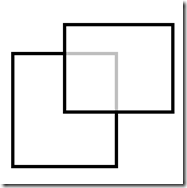
这是最简单的4种遮挡情况，而复杂的遮挡情况总可以通过矩阵分割得到上面几种情况，举个例子：

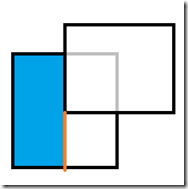
对于这样的遮挡，我们可以这样分割：

把这种情况看成是情况1进行处理，先处理蓝色的部分，对于右边部分进行递归，按照情况3进行处理，其他所有的遮挡情况均可类似分割。

值得注意的是以下的遮挡情况：

我们需要进行如下切割：

这个需要对切割时的判断条件进行精确的描述。

到此，我们已经找到了处理遮挡的一般方法，下面进行总结：

1.我们可以从最底部，也可以从最顶部开始处理每个矩阵，这里采用从最底部的矩阵开始处理；

2.枚举每一个矩阵，与当前处理的矩阵进行遮挡处理，这个遮挡处理的递归终止条件是分割的小矩阵已处于最顶部；

3.统计每个颜色的面积。

给出核心代码：

void cover(int lx,int ly,int ux,int uy,int col,int k)  //(lx,ly)左下角,(ux,uy)右上角，下面的数组类似
{
    while (k<=n && (llx[k]>=ux || urx[k]<=lx || lly[k]>=uy || ury[k]<=ly))
        k++;
    if (k>n) { S[col]+=((ux-lx)*(uy-ly)); return; }
    if (lx<=llx[k]) { cover(lx,ly,llx[k],uy,col,k+1); lx=llx[k]; }  //情况1
    if (ly<=lly[k]) { cover(lx,ly,ux,lly[k],col,k+1); ly=lly[k]; }  //情况3
    if (ux>=urx[k]) { cover(urx[k],ly,ux,uy,col,k+1); ux=urx[k]; }  //情况2
    if (uy>=ury[k]) { cover(lx,ury[k],ux,uy,col,k+1); uy=ury[k]; }  //情况4
}

其实对于每个情况都有几种判断方法，比如情况1，可以写(lx<=llx[k])，也可以写成(ux<=urx[k])，还有(llx[k]<=ux)，但是后面的两种判断并不准确，比如说(llx[k]<=ux)也可以用来表示情况2，所以这里的几个条件一定要重视。

更具体的代码：

/*
ID:ay27272
PROG:rect1
LANG:C++
*/

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define NN 1005

int llx[NN],lly[NN],urx[NN],ury[NN],color[NN];

int S[NN];
int n;

void cover(int lx,int ly,int ux,int uy,int col,int k)
{
    while (k<=n && (llx[k]>=ux || urx[k]<=lx || lly[k]>=uy || ury[k]<=ly))
        k++;
    if (k>n) { S[col]+=((ux-lx)*(uy-ly)); return; }
    if (lx<=llx[k]) { cover(lx,ly,llx[k],uy,col,k+1); lx=llx[k]; }
    if (ly<=lly[k]) { cover(lx,ly,ux,lly[k],col,k+1); ly=lly[k]; }
    if (ux>=urx[k]) { cover(urx[k],ly,ux,uy,col,k+1); ux=urx[k]; }
    if (uy>=ury[k]) { cover(lx,ury[k],ux,uy,col,k+1); uy=ury[k]; }
}

int main()
{
    freopen("rect1.in","r",stdin);
    freopen("rect1.out","w",stdout);
    int X,Y,max_color=0;
    cin>>X>>Y>>n;
    for (int i=1;i<=n;i++)
    {
        scanf("%d%d%d%d%d",&llx[i],&lly[i],&urx[i],&ury[i],&color[i]);
        if (color[i]>max_color) max_color=color[i];
    }

    memset(S,0,sizeof(S));

    for (int i=1;i<=n;i++)
        cover(llx[i],lly[i],urx[i],ury[i],color[i],i+1);

    S[1]=X*Y;
    for (int i=2;i<=max_color;i++)
        S[1]-=S[i];
    for (int i=1;i<=max_color;i++)
        if (S[i]) cout<<i<<" "<<S[i]<<endl;
    return 0;
}