平衡树 替罪羊树(Scapegoat Tree)
替罪羊树(Scapegoat Tree)
题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入xx数
- 删除xx数(若有多个相同的数,因只删除一个)
- 查询xx数的排名(排名定义为比当前数小的数的个数+1+1。若有多个相同的数,因输出最小的排名)
- 查询排名为xx的数
- 求xx的前驱(前驱定义为小于xx,且最大的数)
- 求xx的后继(后继定义为大于xx,且最小的数)
输入格式
第一行为n,表示操作的个数,下面n行每行有两个数opt和x,opt表示操作的序号( 1≤opt≤6 )
输出格式
对于操作3,4,5,6每行输出一个数,表示对应答案
输入样例
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598输出样例
106465
84185
492737数据范围
1.n的数据范围: n≤100000
2.每个数的数据范围: [-10^7, 10^7]
网上的资料比较琐碎难懂,之前看了很多资料一直不能理解平衡树(我太弱了)……前几天突然莫名其妙明白了,想写一篇笔记记录一下(乱写一通)。
0x00 二叉查找树
要初步弄懂平衡树,首先要知道这是一棵二叉查找树。
二叉查找树(Binary Search Tree),当然也可以叫它二叉搜索树,或者二叉排序树(反正都一个意思都是二叉树),它的定义如下:
或者是一棵空树,或者是具有下列性质的二叉树:
差不多就像下面这幅图一样:
0x01 平衡树的用途
在学平衡树这个数据结构前,相信我们一定会先有个问题:平衡树能拿来干什么?
网上的很多资料对这一点写得不太明白(也可能是我太弱了),我先试着乱总结一下:
现在需要一种数据结构,它需要做到以下几点:
1. 高效地查询一个序列中某个数的前面和后面的数(a[i-1]和a[i+1])。
2. 高效地知道第i个数是什么(即a[i])。
3. 高效地插入和删除。
显然,我们可以用普通数组优秀地完成第1点和第2点,但第3点不能够了。当然,我们也可以用链表,复杂度O(1)优秀地完成第1点和第3点,但是对于第2点,链表的复杂度就达到了不太理想的O(n)。
那我们能不能想办法优化一下链表呢?
我们可以回头看一下二叉搜索树的定义,然后我们会发现,假设存在一个从1到8的链表(就像下图,win自带画图画的,不太好看)
其实它也满足左边小于右边的定义,也可以勉强算是一棵以序号为每个节点的权值的二叉查找树。
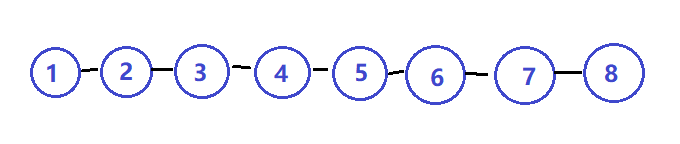
但是这样的一棵二叉树是不是很难看很畸形?
我们怎么想办法把它变成一棵比较好看的树呢?
可以拿笔画画看:
我们尝试把中间的节点(4或者5,我选择4)拎出来,然后就变成了这样:
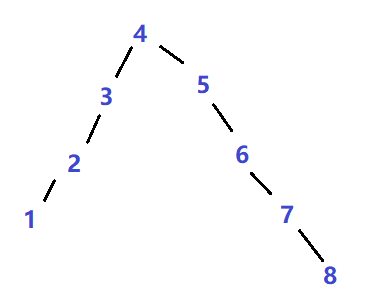
是不是好看了一点?有点树的形状了,那我们可以尝试继续把两侧链上的中间节点继续拎出来,不断重复,最终会变成一棵比较好看的树。
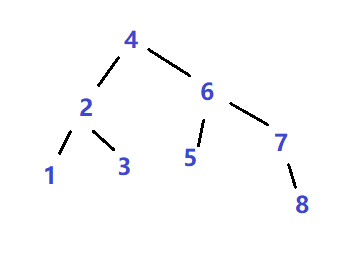
这就是平衡二叉树,严格遵守了二叉查找树的定义——左儿子小于右儿子。
也许你会有疑问:长成这样的一棵树,怎么做到刚刚链表都不能完全做到的3点要求呢?
让我们再看看这棵树:
0x02 查询前驱和后驱
对于一个我们已知的节点i,我们先定义与它深度相同的都是它的兄弟节点。
那么很显然,i的左兄弟及其子树上的所有节点都比i的左儿子及其子树上的所有节点来得小,且i的左儿子及其子树上的所有点都比i的父亲更大,所以显然,i的前驱要在i的左儿子及其子树上找。
同理,仔细观察图,会发现我们所要找的前驱,存在于i的左儿子子树的最右侧,就是i的左儿子的右儿子的右儿子的右儿子的右儿子……(直到最后一个右儿子)
这样,我们就可以O(log n)地求出i的前驱了。i的后驱同理。
0x03 查询第i个数
前面说过,我们用数的序列编号作为节点的排序权值,所以我们只要像线段树那样从根部开始查一遍就可以了。详细解释:
从根结点开始,如果第i个数比当前节点j的序号小,就往左儿子搜,反之右儿子。直到找到第i个数,时间复杂度还是O(log n)。
0x04 插入和删除
插在原序列的末尾,所以新节点的编号是n+1。然后我们把这个节点变成根结点的右儿子的右儿子的右儿子……(变成最后一个没有右儿子的节点的右儿子)。
删除。其实就是把i节点打个被删除掉的标记(甚至不打也可以)。然后让i的左右儿子之一成为i的父节点的新儿子(就是让某一个儿子取代i节点)。复杂度同O(log n)
基本操作差不多就是这样。
那么其实还有一个问题:如果操作太多,导致一棵本来平衡的树变成了一条链表,复杂度爆炸,怎么办呢?
0x05 重新建树
如果你选择的是替罪羊树,那就是优雅的暴力了。替罪羊树在每个节点上记录子树的节点数size,同时还有一个平衡因子alpha(通常在0.5左右,我选择0.7),当每次更新后,递归回去检查i节点的左右儿子分别乘以平衡因子,是否大于另一个儿子,如果大了,代表这棵树有退化的倾向,赶紧拍平重建(就是把树压成链表,重新建树)。
大概就是这样,手机打的好难受,直接上代码好了。
(其实我一开始做平衡树时觉得可以用线段树模拟的emmm,就不说了)
代码可以配合洛谷的模板题食用
#include <cstdio> #include <iostream> using namespace std; const int INF=1000000000; const int MAX_N=2000005; const double alpha=0.75; int n; inline int read(){ register int ch=getchar(),x=0,f=1; while (ch<'0'||ch>'9'){ if (ch=='-') f=-1; ch=getchar(); } while (ch>='0'&&ch<='9'){ x=x*10+ch-'0'; ch=getchar(); } return x*f; } struct Tree{ int fa; int size; int value; int son[2]; }tree[MAX_N]; int cnt=2; int root=1; int node[MAX_N]; int sum; bool balance(int x){ //判断是否平衡 return (double)tree[x].size*alpha>=(double)tree[tree[x].son[0]].size&&(double)tree[x].size*alpha>=(double)tree[tree[x].son[1]].size; } int build(int l,int r){ //重新递归建树 if (l>r) return 0; int mid=(l+r)>>1; tree[tree[node[mid]].son[0]=build(l,mid-1)].fa=node[mid],tree[tree[node[mid]].son[1]=build(mid+1,r)].fa=node[mid]; tree[node[mid]].size=tree[tree[node[mid]].son[0]].size+tree[tree[node[mid]].son[1]].size+1; return node[mid]; } void recycle(int x){ //把树压成数列 if (tree[x].son[0]) recycle(tree[x].son[0]); node[++sum]=x; if (tree[x].son[1]) recycle(tree[x].son[1]); } void rebuild(int x){ sum=0; recycle(x); int fa=tree[x].fa,son=(tree[tree[x].fa].son[1]==x),now=build(1,sum); tree[tree[fa].son[son]=now].fa=fa; if (x==root) root=now; } void insert(int x){ int i=root,now=++cnt; //新节点序号 tree[now].size=1,tree[now].value=x; while (true){ tree[i].size++; bool son=(x>=tree[i].value); if (tree[i].son[son]) i=tree[i].son[son]; else{ tree[tree[i].son[son]=now].fa=i; break; } } int flag=0; for (int j=now;j;j=tree[j].fa) //logn找不平衡的节点 if (!balance(j)) flag=j; if (flag) rebuild(flag); //重建树 } int get_num(int x){ int i=root; while (true){ if(tree[i].value==x) return i; else i=tree[i].son[tree[i].value<x]; } } void erase(int x){ //删除 if (tree[x].son[0]&&tree[x].son[1]){ int now=tree[x].son[0]; while (tree[now].son[1]) now=tree[now].son[1]; tree[x].value=tree[now].value; x=now; } int son=(tree[x].son[0])?tree[x].son[0]:tree[x].son[1]; int k=(tree[tree[x].fa].son[1]==x); tree[tree[tree[x].fa].son[k]=son].fa=tree[x].fa; for (int i=tree[x].fa;i;i=tree[i].fa) tree[i].size--; if (x==root) root=son; } int get_rank(int x){ int i=root,ans=0; while (i) if(tree[i].value<x) ans+=tree[tree[i].son[0]].size+1,i=tree[i].son[1]; else i=tree[i].son[0]; return ans; } int get_kth(int x){ int i=root; while (true) if (tree[tree[i].son[0]].size==x-1) return i; else if (tree[tree[i].son[0]].size>=x) i=tree[i].son[0]; else x-=tree[tree[i].son[0]].size+1,i=tree[i].son[1]; return i; } int get_front(int x){ int i=root,ans=-INF; while(i) if(tree[i].value<x) ans=max(ans,tree[i].value),i=tree[i].son[1]; else i=tree[i].son[0]; return ans; } int get_behind(int x){ int i=root,ans=INF; while(i) if(tree[i].value>x) ans=min(ans,tree[i].value),i=tree[i].son[0]; else i=tree[i].son[1]; return ans; } int main(){ // freopen("test1.in","r",stdin); tree[1].value=-INF,tree[1].size=2,tree[1].son[1]=2; tree[2].value=INF,tree[2].size=1,tree[2].fa=1; n=read(); for(int i=1,op,x;i<=n;i++){ op=read(),x=read(); if(op==1) insert(x); if(op==2) erase(get_num(x)); if(op==3) printf("%d\n",get_rank(x)); if(op==4) printf("%d\n",tree[get_kth(x+1)].value); if(op==5) printf("%d\n",get_front(x)); if(op==6) printf("%d\n",get_behind(x)); } }
其他例题
大体上按难度排序?我太弱了也搞不懂。
一.[HNOI2002]营业额统计 (2019.4.10更新)
据说有各种神犇用许多神奇的解法A掉了……但是我这种蒟蒻就先用平衡树练手了。
min{|该天以前某一天的营业额-该天营业额|},即不大于a[i]的最大值和不小于a[i]的最小值,就是寻找a[i]的前驱和后驱,分别减去a[i]取绝对值,再全部加起来,复杂度应该是O(nlogn)。
代码:
#include <cstdio> #include <iostream> using namespace std; const int INF=1000000000; const int MAX_N=2000005; const double alpha=0.75; int n; inline int read(){ register int ch=getchar(),x=0,f=1; while (ch<'0'||ch>'9'){ if (ch=='-') f=-1; ch=getchar(); } while (ch>='0'&&ch<='9'){ x=x*10+ch-'0'; ch=getchar(); } return x*f; } struct Tree{ int fa; int size; int value; int son[2]; }tree[MAX_N]; int cnt=2; int root=1; int node[MAX_N]; int sum; bool balance(register int x){ //判断是否平衡 return (double)tree[x].size*alpha>=(double)tree[tree[x].son[0]].size&&(double)tree[x].size*alpha>=(double)tree[tree[x].son[1]].size; } inline int build(register int l,register int r){ //重新递归建树 if (l>r) return 0; int mid=(l+r)>>1; tree[tree[node[mid]].son[0]=build(l,mid-1)].fa=node[mid],tree[tree[node[mid]].son[1]=build(mid+1,r)].fa=node[mid]; tree[node[mid]].size=tree[tree[node[mid]].son[0]].size+tree[tree[node[mid]].son[1]].size+1; return node[mid]; } void recycle(register int x){ //把树压成数列 if (tree[x].son[0]) recycle(tree[x].son[0]); node[++sum]=x; if (tree[x].son[1]) recycle(tree[x].son[1]); } void rebuild(register int x){ sum=0; recycle(x); int fa=tree[x].fa,son=(tree[tree[x].fa].son[1]==x),now=build(1,sum); tree[tree[fa].son[son]=now].fa=fa; if (x==root) root=now; } void insert(register int x){ int i=root,now=++cnt; //新节点序号 tree[now].size=1,tree[now].value=x; while (true){ tree[i].size++; bool son=(x>=tree[i].value); if (tree[i].son[son]) i=tree[i].son[son]; else{ tree[tree[i].son[son]=now].fa=i; break; } } int flag=0; for (int j=now;j;j=tree[j].fa) //logn找不平衡的节点 if (!balance(j)) flag=j; if (flag) rebuild(flag); //重建树 } inline int get_front(register int x){ register int i=root,ans=-INF; while(i) if(tree[i].value<x) ans=max(ans,tree[i].value),i=tree[i].son[1]; else i=tree[i].son[0]; return ans; } inline int get_behind(register int x){ register int i=root,ans=INF; while(i) if(tree[i].value>x) ans=min(ans,tree[i].value),i=tree[i].son[0]; else i=tree[i].son[1]; return ans; } bool flag[1000000+5]; int result; int main(){ // freopen("test1.in","r",stdin); tree[1].value=-INF,tree[1].size=2,tree[1].son[1]=2; tree[2].value=INF,tree[2].size=1,tree[2].fa=1; n=read(); int kkk=read(); result+=kkk; insert(kkk); flag[kkk]=true; for (int i=2,a,min,max;i<=n;i++){ a=read(); if (flag[a]) continue; flag[a]=true; insert(a); min=get_front(a); max=get_behind(a); if (min==-INF){ result+=(max-a); continue; } else if (max==INF){ result+=(a-min); continue; } result+=(a-min>max-a?max-a:a-min); } printf("%d",result); return 0; }
[学习自百度百科和其他网络资料]



