排列组合是算法常用的基本工具,如何在c语言中实现排列组合呢?思路如下:
首先看递归实现,由于递归将问题逐级分解,因此相对比较容易理解,但是需要消耗大量的栈空间,如果线程栈空间不够,那么就运行不下去了,而且函数调用开销也比较大。
(1) 全排列:
全排列表示把集合中元素的所有按照一定的顺序排列起来,使用P(n, n) = n!表示n个元素全排列的个数。
例如:{1, 2, 3}的全排列为:
123;132;
213;231;
312;321;
共6个,即3!=3*2*1=6。
这个是怎么算出来的呢?
首先取一个元素,例如取出了1,那么就还剩下{2, 3}。
然后再从剩下的集合中取出一个元素,例如取出2,那么还剩下{3}。
以此类推,把所有可能的情况取一遍,就是全排列了,如图:
知道了这个过程,算法也就写出来了:
将数组看为一个集合,将集合分为两部分:0~s和s~e,其中0~s表示已经选出来的元素,而s~e表示还没有选择的元素。
perm(set, s, e)
{
顺序从s~e中选出一个元素与s交换(即选出一个元素)
调用perm(set, s + 1, e)
直到s>e,即剩余集合已经为空了,输出set
}
c语言代码如下:
void perm(int list[], int s, int e, void (*cbk)(int list[]))
{
int i;
if(s > e)
{
(*cbk)(list);
}
else
{
for(i = s; i <= e; i++)
{
swap(list, s, i);
perm(list, s + 1, e, cbk);
swap(list, s, i);
}
}
}
其中:
void swap(int * o, int i, int j)
{
int tmp = o[i];
o[i] = o[j];
o[j] = tmp;
}
cbk是回调函数,可以写成:
void cbk_print(int * subs)
{
printf("{");
for(int i = 0; i < LEN; i++)
{
printf("%d", subs[i]);
(i == LEN - 1) ? printf("") : printf(", ");
}
printf("}\n");
}
(2)组合:
组合指从n个不同元素中取出m个元素来合成的一个组,这个组内元素没有顺序。使用C(n, k)表示从n个元素中取出k个元素的取法数。
C(n, k) = n! / (k! * (n-k)!)
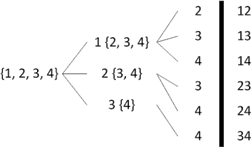
例如:从{1,2,3,4}中取出2个元素的组合为:
12;13;14;
23;24;
34
方法是:先从集合中取出一个元素,例如取出1,则剩下{2,3,4}
然后从剩下的集合中取出一个元素,例如取出2
这时12就构成了一个组,如图。
从上面这个过程可以看出,每一次从集合中选出一个元素,然后对剩余的集合(n-1)进行一次k-1组合。
comb(set, subset, n, k)
{
反向从集合中选出一个元素,将这个元素放入subset中。
调用comb(set, subset, n-1, k-1)
直到只需要选一个元素为止
}
C语言代码如下:
void combine(int s[], int n, int k, void (*cbk)(int * subset, int k))
{
if(k == 0)
{
cbk(subset, k);
return;
}
for(int i = n; i >= k; i--)
{
subset[k-1] = s[i-1];
if(k > 1)
{
combine(s, i-1, k-1, cbk);
}
else
{
cbk(subset, subset_length);
}
}
}
任何递归算法都可以转换为非递归算法,只要使用一个栈模拟函数调用过程中对参数的保存就行了,当然,这样的方法没有多少意思,在这里就不讲了。下面要说的是用其它思路实现的非递归算法:
(1)全排列:
首先来看一段代码:
#include <iostream>
#include <algorithm>
using namespace std;
int main () {
int myints[] = {1,2,3};
cout << "The 3! possible permutations with 3 elements:\n";
sort (myints,myints+3);
do {
cout << myints[0] << " " << myints[1] << " " << myints[2] << endl;
} while ( next_permutation (myints,myints+3) );
return 0;
}
这段代码是从STL Permutation上考下来的,要注意的是第10行,首先对数组进行了排序。
第14行的next_permutation()是STL的函数,它的原理是这样的:生成当前列表的下一个相邻的字典序列表,里面的元素只能交换位置,数值不能改变。
什么意思呢?
123的下一个字典序是132,因为132比123大,但是又比其他的序列小。
算法是:
(1) 从右向左,找出第一个比右边数字小的数字A。
(2) 从右向左,找出第一个比A大的数字B。
(3) 交换A和B。
(4) 将A后面的串(不包括A)反转。
就完成了。
好,现在按照上面的思路,写出next_permutation函数:
template <class T>
bool next_perm(T * start, T * end)
{
//_asm{int 3}
if (start == end)
{
return false;
}
else
{
T * pA = NULL, * pB;
T tmp = * end;
// find A.
for (T * p = end; p >= start; p--)
{
if (*p < tmp)
{
pA = p;
break;
}
else
{
tmp = *p;
}
}
if (pA == NULL)
{
return false;
}
// find B.
for (T * p = end; p >= start; p--)
{
if (*p > *pA)
{
pB = p;
break;
}
}
// swap A, B.
tmp = *pA;
*pA = *pB;
*pB = tmp;
// flip sequence after A
for (T *p = pA+1, *q = end; p < q; p++, q--)
{
tmp = *p;
*p = *q;
*q = tmp;
}
return true;
}
}
(2)组合:01交换法
使用0或1表示集合中的元素是否出现在选出的集合中,因此一个0/1列表即可表示选出哪些元素。
例如:[1 2 3 4 5],选出的元素是[1 2 3]那么列表就是[1 1 1 0 0]。
算法是这样的:
comb(set, n, k)
{
(1) 从左到右扫描0/1列表,如果遇到“10”组合,就将它转换为”01”.
(2) 将上一步找出的“10”组合前面的所有1全部移到set的最左侧。
(3) 重复(1) (2)直到没有“10”组合出现。
}
代码如下:
template<class T>
void combine(T set[], int n, int k, void (*cbk)(T set[]))
{
unsigned char * vec = new unsigned char[n];
T * subset = new T[k];
// build the 0-1 vector.
for(int i = 0; i < n; i++)
{
if (i < k)
vec[i] = 1;
else
vec[i] = 0;
}
// begin scan.
bool has_next = true;
while (has_next)
{
// get choosen.
int j = 0;
for (int i = 0; i < n; i++)
{
if (vec[i] == 1)
{
subset[j++] = set[i];
}
}
cbk(subset);
has_next = false;
for (int i = 0; i < n - 1; i++)
{
if (vec[i] == 1 && vec[i + 1] == 0)
{
vec[i] = 0;
vec[i + 1] = 1;
// move all 1 to left-most side.
int count = 0;
for (int j = 0; j < i; j++)
{
if (vec[j] == 1)
count ++;
}
if (count < i)
{
for (int j = 0; j < count; j++)
{
vec[j] = 1;
}
for (int j = count; j < i; j++)
{
vec[j] = 0;
}
}
has_next = true;
break;
}
}
}
delete [] vec;
delete [] subset;
}
至于其中的道理,n个位置上有k个1,按照算法移动,可以保证k个1的位置不重复,且覆盖n一遍。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号