信息论中的熵（信息熵，联合熵，交叉熵，互信息）和最大熵模型
摘要：
1.信息的度量
2.信息不确定性的度量
内容：
1.信息的度量
直接给出公式
，这里的N(x)是随机变量X的取值个数，至于为什么这么表示可以考虑以下两个事实：
（1）两个独立事件X,Y的联合概率是可乘的，即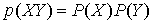
，而X,Y同时发生的信息量应该是可加的，即
，因此对概率取了负对数（保证非负）
（2）一个时间发生的概率越大，其信息量越小，因此对概率取了负对数（保证非负）
举两个例子便于理解：
一本50w字的史记的最大信息量是-ln(1/50w),2010年世界杯32支队伍谁会夺冠的最大信息量是-ln(1/32);注意：这里的ln是以2为底的，信息的单位是bit，并且都是假定概率分布都是均匀分布的，之后再解释为什么假设为均匀分布。
总结：直观理解其实就是给信息编码的过程，比如数字0-9的二进制表示只要ln10
2.信息不确定性的度量
直接给出公式
，也就是信息量的期望；这个值叫做熵
以下讨论几个分布：
对于最简单的0-1分布，假设p(x=1)=p,则p(x=0)=1-p，计算信息熵：
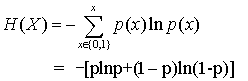
对于均匀分布，假设p(x=n)=1/N,其中N是随机变量的取值个数，计算信息熵：
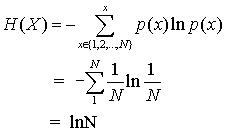
不加证明的给出结论：随机变量为定值时，熵最小；随机变量为均匀分布时，熵最大
讨论下二元随机变量的情况，为了直观解释和记忆，先给出如下图解：
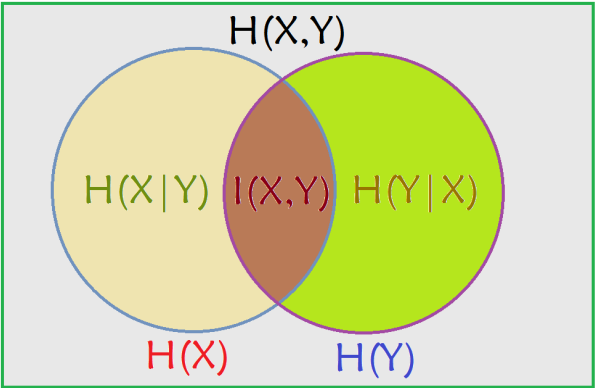
先说联合熵的定义，代表X,Y同时发生的不确定性；公式为
，从上图中理解就是两个大圆的面积。
再说条件熵，代表在已知一个变量发生的条件下，另一个变量发生所新增的不确定性；公式为：
，有兴趣的朋友可以自己推导一下是如何从（1）式到（2）式的，从上图中理解就是两个大圆去掉其中一个大圆所剩下的面积。
最后定义互信息，其中的一个定义就是在已知X发生的条件下，Y不确定性减少的程度，这个定义在ID3算法中也叫信息增益，计算公式可以理解为：
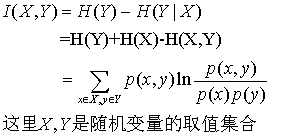，有兴趣的朋友可以自己推导一下是如何从（1）式到（2）式的，从上图理解就是两个大圆相交的面积，所以互信息是对偶的。
另一个定义是这样：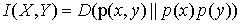
，等式右边的值叫做KL散度，相对熵，或者交叉熵等等，所以说理解了交叉熵就理解了互信息的第二个定义。
定义交叉熵，代表两个概率分布（函数）的相似度，计算公式为：
最后要解释的是最大熵的思想，最大熵原理指出，需要对一个随机事件的概率分布进行预测是，我们的预测应当满足全部已知的条件，未知的部分概率应该是均匀的，这样预测的风险最小，因为这时的信息熵最大，所以称这种模型为最大熵模型。举一个例子，如果没有任何已知条件下问你投一个骰子，出现5点的概率多大，这时假定所有的点数出现的概率是相等的一定是一种最保险的方法，这就是最大熵模型。
ok,最后一步，最大熵的目标函数/模型函数：
最大熵的推导，首先是最大熵模型的数学描述：
简述推导如下：
上面是通过拉格朗日乘数法求解的，也可以通过对数极大似然估计推导
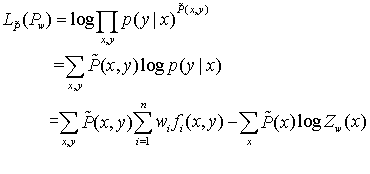
最大熵模型的实现方法：GIS和IIS
最大熵模型的应用：语言标注；文本分类；语言处理中的其他应用
